测量结果表达式与不确定度关系的研究与探讨

张锐波

（浙江大学，杭州舟山 310015）

测量结果表达式与不确定度关系的研究与探讨

张锐波

（浙江大学，杭州舟山 310015）

测量不确定度和结果表达是学习物理实验的重要概念，它是衡量测量结果可靠性和准确程度的标志。本文就这些概念以及它们之间关系一一进行阐述，以有利于学生学习与参考。

测量；结果表达；不确定度；随机误差；系统误差

测量者欲获得该待测物理量的最佳值是很困难的，尽管采用了尽可能多的有效手段企图减小测量过程中可能产生的各种误差，诸如必须的等精度测量，对实验仪器缜密调节与增加测量次数等，都无异于提高实验测量精度，原于学生往往忽视对测量过程中存在的已定系统误差纠正与测量物理量真值所处范围（不确定度）估测以及测量结果的正确表达。

1 书写测量结果表达式的前提条件

“真值只有定义严密时通过完善的测量才可能获得，它一般无从获知”［1－3］，其实，真值在任何条件下都无法获得，也没有特殊的可能。为此，考虑给予真值存在的范围（或区间）有根据地估测非常有必要。

1.1 结果表达式的物理涵义

测量某一物理量，它的真值所处范围必须用测量结果表达式来表达，其表达形式

图1 为结果表达式示意图

1.2 测量结果的表达思路

然后，再考虑剩余未定系差，其与统计规律产生的标准差一同放入不确定度内，用来表示测量真值的存在范围 －不确定度。图2所示。

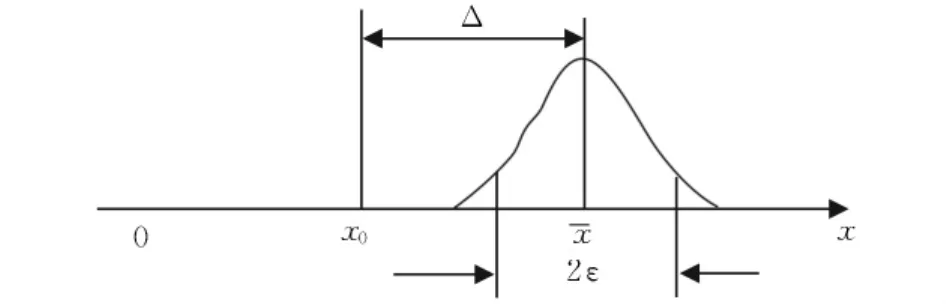
图2 系统误差与随即误差关系

1.3 测量值已定系差的修正

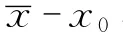
举一个简单的例子，若用精度1／100秒表测量某同学的百米用时，该同学听见枪开始起跑，同时冲刺线处老师开始计时，跑至冲刺线计时结束，成绩为14.44秒，根据声音在空气中的传播速度340m／s，存在系差s／v＝100／340＝0.294秒，因此，该同学的百米测试成绩修正为14.146秒。又如用螺旋测微器测一工件厚度，测脚吻合时初值为x0（不为零），该情况下必须对测值结果进行修正。

2 物理实验中不确定度估测分类概述

不确定度表明的是被测值的分散性，无法准确获知以便对测量结果进行修正的一种未定系差，该值大致范围只能凭借经验或仪器的生产厂家提供。

2.1 不同类不确定度分量来源涵义与估测

（1）制造厂家对某种型号仪器所规定的示值误差的允许范围，而不是某一台仪器实际存在的误差。测量仪器的最大允许误差可在仪器说明书或名牌中查到，用数值表示时有正负之分，通常采用绝对误差、相对误差、引用误差或它们的组合形式来表示。一般采用仪器的准确度等级（或级别）来估算，诸如惠斯通电桥在不同测值范围准确度等级，则准确度就为“级别%”，仪器误差Δ仪＝最佳测量值×级别%。

（2）测量结果中由测量仪器引入的不确定度可依该仪器最大允许误差来评定，它是采用计量局更精密的测量仪器测量同一物理量，然后进行比对来标定该仪器的仪器误差。制造厂家一般将其标注在仪器说明书（手册）或铭牌上，大多数仪器设备都会有不同测值范围内的仪器误差。例如，螺旋测微器误差0.004mm、毫米尺上标定的0.1mm等等；

（3）千分尺与角游标尺类型仪器，由于它们读数的特点均是依据游标尺某刻线与主尺某刻线重合（即同一条直线）来读数，则仪器误差均为其最小分格（或称精度）。如此，还有电子秤、频率计、数字电压电流表、秒表等；

（4）凡存在估读类的测量仪器，其仪器误差均为该仪器最小分格（或精度）的一半，除非在该测量仪器上明确标注仪器误差为多少，此属第二种情况。诸如，螺旋测微器最小分格为0.01mm，仪器误差为0.005mm；如此，还有皮尺、钢尺、光速测定装置标尺、显微镜游标尺、迈克尔逊游标尺、示波器荧光屏最小分格等。此在于测量者在对相关最小分格估读时，虽然存在随机性，其都不会超出最小分格的二分之一所致；

减小未定系统误差，只能通过改进和精心调节实验仪器，尽可能地提高测量精度，使之测量值尽可能地接近真值，进而减小测量真值的表示范围（区间），最大限度地提高测量值的置信概率。

2.2 不确定度分量的方和根合成

不确定度按其获得渠道可分为A、B类分量。A类分量拟采用统计分析方法评定，即标准差（测量次数n≥2）评定；B类分量称为隐含着的可估计值，它不能对测量值加以修正，仅能对已修正测量值的不完善而引入的量值归并入不确定度中，以表示真值所处范围。它是依据经验、资料或其他信息来估算，一般采用均匀分布（ΔBi）较为合适。其方和根合成公式

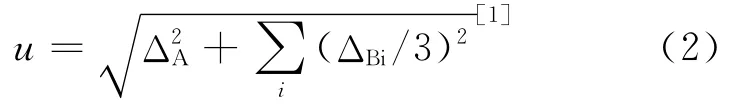
应该特别指出的是惠斯登电桥测电阻，一些同学错误地把由于检流计灵敏度与电阻箱引起的误差合成只是简单地采用Rx1＋Rx2代数和来处理［1］，是没有道理的。

2.3 扩展不确定度与置信概率的关系

为科学地表示真值所处范围（区间），如图1所示，通常采用总不确定度U＝ciu表示，它是采用合成不确定度 的延展（或拓展）而来，其中ci（i＝1、2、3）为延展系数，ci值愈大，真值所处范围的置信概率就越高，严格来讲ci值由自由度确定，实际教学中，拟采用c＝2或3，其置信概率分别为95.5%和99.7%，此处c的取值自随即误差正态分布2ε、3ε拓展，此处我持反对意见，因u是标差与未定系差合成而来，并非满足正态分布规律，置信概率的随便套用是不科学的，为此，应向学生说明［2］。

3 结果表达式的正确书写

3.1 扩展不确定度（U）有效数据的保留

总不确定度U（ciu）有效数据保留几位，传统的方法是首位非零数≤3取两位、首位数非零＞3取一位［1］。比如：U＝0.210 1，应保留为0.22；U＝0.410 1，应保留为0.5。上述均是由上述均在保留位加1是由于留位后有数，其原因在于如图1所示，以提高真值在该范围置信概率，以不失去结果表达式的物理含义。

清华大学牛鹤年老师关于对U的修约是“首位数字较小（如1、2等）时一般取两位，不小于5时通常取1位”［3］，为此，我建议不确定度取位大家应该有一个统一标准。

3.2 测量值有效数据的保留

结果表达式中测量值有效数据位数也有严格修约，传统的方法拟采用与合成不确定度相同数量级的保留位数，保留位以5为限，大者进1，小者不进，等者视其前为奇者进、偶者舍的保留模式。

3.3 结果表达式书写举例

结果表达的形式如（1）式所示，关键是要对测量值的系统误差进行纠正，并按上述规范推算不确定，以及实际表达时的系微变化。

需要说明的是，若（3）式套用规范x＝（6.5687±0.0036）mm是不正确的，因测量值估读至10-3mm，总不确定度（U）按规范有效数字保留至10-4mm已没必要，此时应以测量值估读末位为准，故总不确定度应保留1位。通常情况，作者主张伸展不确定度c取3较为合适。

4 结 论

数据处理与结果表达是物理实验教学中的重要环节，是实验成功与否重要标志。本文系统地分析和阐述了（1）表达式书写形式、相关因素、一维图示及其物理涵义；（2）在测量某一物理量时，举例说明、发现、纠正系统误差是测量结果表达的关键，并用图示说明了系统误差与随机误差是“西瓜与芝麻”之关系；（3）不确定度是标准误差偏差与未定系统误差合成，尤其未定系差的4种来源归类与估算方法；（4）提出了扩展（伸展）不确定概念，及其与置信概率类比拓展关系；（5）结果表达时测量值与总不确定度有效数据位数的理论依据与实际应用时的灵活性。

［1］ 陈守川等.新编大学物理实验教程［M］.浙江：浙江大学出版社，2011：114.

［2］ 方心 张锐波.误差理论几个问题的讨论［J］.大学物理实验.2011，24（6）：86-89.

［3］ 牛鹤年.新概念物理实验测量引论［M］.北京：高等教育出版社，2007.

Research on the Relationship between Expression and Uncertainty of Measuring Result

ZHANG Rui-bo

（Zhejiang University，Hangzhou 310015）

The expression of measuring result and uncertainty are the important concept in the processes of physical experiment study.They also are the important standard to judge the degree of reliability and accuracy of measuring result.In this paper，these concepts and their relation were discussed one by one.These concepts explaining and deriving are beneficial to student’s study.

measurement；result expression；uncertainty；random error；systematic error

O4-8

A

1007-2934（2012）03-0100-03

2011-12-11