旋转电机铁耗模型及在双凸极电机中的应用
2012-12-06孟小利
李 江,钱 乐,侯 栋,孟小利
(南京航空航天大学,江苏南京210016)
0 引 言
随着电气设备能源利用率的提高,降低损耗、提升效率逐渐成为一个重要的研究方向。电机的损耗主要分为铁心损耗、绕组铜耗以及机械损耗[1]。其中铁心损耗占据比例较大,它的准确计算已成为电机设计及其性能优化时不可或缺的部分。
电机的类型,定转子结构、转速、控制策略以及铁心材料的特性等对电机中的磁场都有直接的影响。由于漏磁及磁饱和的存在,铁心中磁密波形是非正弦、非线性的。铁耗的计算是以磁密的波形信息为基础,因而电机磁场模型、铁心磁密波形的准确建立和获取十分必要。
研究铁耗的成因和组成是铁耗建模的关键。Bertotti 于文献[2]中根据产生机理建立了包括磁滞、涡流和杂散损耗(Excess Loss)的铁耗计算模型,但该模型只适用于正弦波形的交变磁场;Zhu J.G.考虑到电机运转中磁化方式的复杂性,通过二维铁耗测试设备测量出的铁耗数据建立了旋转磁化损耗模型[3],具有较高的精度,但目前该设备还未普及;B.Stumberger 尝试用两个相互正交的交变磁场来等效旋转磁场[4],从而近似地等效旋转磁化下的铁耗,但是未考虑高频状态下硅钢片中磁密集肤效应的影响,当应用于磁密基波频率较高的场合时,计算误差较大;目前绝大部分模型[5-7]中的系数均需要爱普斯坦方圈或者环形样品测试仪测量的铁损数据来拟合得到,这需要进行额外的测量实验。本文在考虑旋转磁化和集肤效应的基础上,修改优化了传统铁耗模型,并利用双凸极电机的实测铁耗进行模型系数的拟合,实验证实了模型的准确性。
1 电机磁场模型建立
1.1 边值问题
鉴于电机内各部分磁场的复杂性,为获得电机运转中定转子准确的磁场信息,本文运用有限元法,通过有限元分析软件ANSYS 对电机进行了模型的建立和磁密的求解。
为降低问题的复杂性,考虑用二维平行平面场有限元法对电机磁场进行分析。计算前进行如下理想假设:求解区域存在电流源,故用矢量磁位进行分析,且忽略端部效应,即A = Az;磁场仅限于电机内部,定子外部边界和转子内部边界为零矢量磁位线;忽略磁滞回环的影响,磁化曲线为单值曲线。
在直角坐标系下,对应的边值问题:

式中:μ 为媒质磁导率;Jz为加在绕组区域的电流密度;边界条件指定子外部边界和转子内部边界。
电流密度的取值如下:

式中:N 为绕组匝数;I 为绕组中每匝电流值;S 为绕组区域面积。对于励磁绕组I 为常数值,而电枢绕组ABC 三相电流I 需要根据相位在每个转子位置处计算得出。
1.2 耦合边界法的运用
本文运用时步有限元法处理定转子相对运动的问题,从而获取电机旋转状态下的磁密波形。为获取任意位置周期上的磁密波形,在每一步的磁场计算中需要保持网格单元的大小和数目一致,此处采用耦合边界法实现。
由于定转子间气隙较小,磁势变化较大,气隙剖分层数越多,计算精度越高,但计算时间也随之增加;为保证计算的准确性,同时提高计算效率,将气隙层剖分为四层网格。中间两层网格在它们公共边界上各自拥有一组节点。两组节点总数相等,记为N,且圆周方向上相邻两节点等间距。对两组节点分别编号,每节点位置处存在两节点,故同一位置处存在双重编号,如图1(a)所示,此处剖分网格为四节点单元。将位置重合处的两个节点进行磁矢位的耦合,即可建立该转子位置的磁场模型。转子转动时,运动模型中转子侧网格及节点将发生偏移,如图1(b)所示,这里偏移了一个节点间距。新位置处重合节点的编号可以根据转动步长和节点间距求出;只要根据转动后重合节点的编号,在静止模型中将两组重合节点再次进行磁矢位的耦合,即可建立新位置的磁场模型,实现了静止模型下转子的等效转动。为保证转动后两组节点重合,转动步长应取为节点间距的整数倍。

图1 转动前后重合节点的编号
选取合理的转动步长,使得转动过程中两组节点能够重合,按照重合节点的编号进行磁矢位的耦合,每次耦合进行一次静磁计算,由此可以获得电机运转过程中定转子周期上的磁密波形,而无需模型的重建。
1.3 磁场参数获取
各位置处磁场模型建立后,相应的边值问题可以等价于条件变分问题,通过泛函的极值条件可以得到所有节点矢量磁位的非线性方程组,然后利用牛顿-拉菲逊法(N-R)进行线性化以及共轭梯度法(CG)对线性方程组求解,得到所有节点的矢量磁位。根据单元节点的矢量磁位Az可以求出单元x、y 方向的磁密分量:

由于各单元磁密大小和方向都是随时间变化的函数,属于旋转磁化范畴[7]。此处对磁密进行两个正交方向的分解,以利于后续的波形处理和损耗的求解。径向和切向磁密Br、Bθ同理也可求得,本文中铁耗即是在径切向磁密的基础上进行的求解。
磁密中还存在大量的谐波分量,而铁耗模型是基于正弦波的磁密进行的计算,所以要进行谐波分析,即相应的傅里叶分解,然后将各次谐波的幅值及频率依次代入铁耗模型进行计算。
2 电机铁耗模型
2.1 铁心磁滞损耗
磁滞损耗是铁心在交变磁化下,内部磁畴不断改变排列方向和发生畴壁位移而造成的能量损耗。正弦波形磁场B = Bmsin(2πft + θ)中铁磁材料单位体积下的磁滞损耗可表示[2]:

式中:Pah为交变磁场中的磁滞损耗;Kh为材料的交变磁滞损耗系数;f 为磁场频率;Bm为正弦磁密波形的幅值;α 为斯坦门兹系数。
对于系数α 而言,一般的选取规则是:当磁密幅值小于1 T 时可取1.6;当磁密幅值大于1 T 时宜取2.0[8]。为了对该系数更准确地取值以及后面计算的需要,考虑用二项式对Bα进行拟合[9]:

式中:系数a、b 为材料性能的比例常数。
一般而言,当磁密在1.0~1.5 T 范围内时,旋转磁滞损耗较之交变磁滞损耗约大45%~65%[1]。考虑用两个正交的交变磁化方式下的铁耗之和等效旋转磁化方式下的铁耗[4]。若将磁密分解为径向和切向分量,旋转磁滞损耗表示:

式中:Pahr、Pahθ分别是径向和切向上的交变磁滞损耗;Br、Bθ分别为径向和切向磁密幅值。
在实际情况中,因为漏磁和磁路饱和的问题,电机中的磁密波形包含大量谐波,需要进行傅里叶分解,并依次求解各次谐波下的磁滞损耗,最后进行相应叠加,所以单位体积下旋转磁滞损耗:

式中:k 为谐波次数;f1为磁密基波频率;Bkr、Bkθ为各次谐波下的径向和切向磁密幅值。
2.2 片状铁心涡流损耗
根据电磁感应原理,变化的磁通在导体中产生旋涡状的感应电流,该电流以焦耳热的形式耗散,即所谓涡流损耗。
根据经典电磁场理论,若忽略铁磁材料磁化曲线的磁滞回环及其非线性,正弦磁场中单片硅钢片的交变涡流损耗[10]推导如:

式中:Ke为交变涡流损耗系数;Kc(f)为考虑高频磁密B 下硅钢片截面磁密出现集肤效应时的修正因子;γ 为硅钢片电导率;d 为硅钢片的厚度;V 为硅钢片的体积,如图2 所示,V =dhl;μ 为平均磁导率;f 为磁密的频率。

图2 硅钢片涡流损耗推导示意图
此时将磁导率μ 看作一常数,可取磁化曲线周期上各点磁导率的平均值,即μ =
同理,考虑磁密径向和切向方向的磁密分解,以及谐波磁密的存在,则单片硅钢片旋转涡流损耗模型:

2.3 总铁耗模型及损耗系数计算
Bertotti 三项铁耗模型中的杂散损耗由于在总损耗中所占的比例较小[11],此处忽略,即电机中铁耗主要由磁滞和涡流损耗构成。在有限元分析中求解的是各单元的磁密信息,所有剖分单元铁耗求和得单片硅钢片的铁耗,再乘以电机轴向硅钢片片数,即为电机总铁耗:
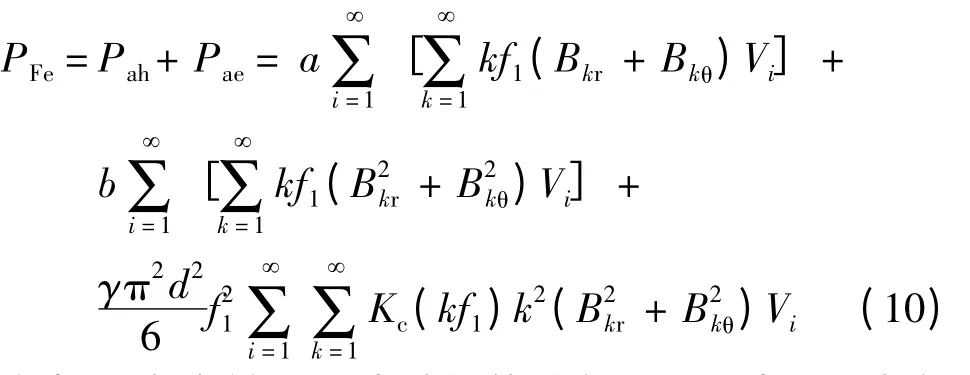
式中:n 为定转子单片硅钢的总剖分单元数;Vi为剖分单元i 的面积Si、电机轴向长度以及叠压系数的乘积。
为了获得电机实际复杂磁化方式下铁耗模型的系数,尝试使用电机铁耗的测量值进行铁耗模型参数的求取。
总铁耗可通过实验测量间接获得,将有限元分析中获取的定转子单元磁密代入式(10),可获得关于系数a、b 的线性方程;通过相同转速、不同励磁电流下多组铁耗数据的线性拟合,即可求取a、b。
3 双凸极电机磁场模型及损耗
3.1 双凸极电机结构
双凸极电机是在改善传统开关磁阻电机性能的基础上发展起来的。它的结构与开关磁阻电机类似,转子上无绕组,但定子中除了电枢绕组外还存在一组永磁体或励磁绕组,相应的称之为永磁双凸极和电励磁双凸极电机。
本文在一台30 /20 三相电励磁双凸极发电机的基础上进行了铁耗的研究,电机结构及绕组分布如图3 所示。双凸极电机空载运行时,励磁绕组加载直流励磁,电枢绕组断接,转子由外部电机的驱动,电机内产生变化的磁场。本文主要在此状态下进行了磁场的建模和铁耗的研究。铁心硅钢片牌号为DW310-35,轴向长度170 mm,叠压系数95%,定子外径400 mm,定转子气隙0.4 mm。

图3 电机结构及绕组分布
3.2 磁场模型的建立及分析
图4 为该双凸极电机定转子的部分网格剖分,其中总单元数为23 640,总节点数75 040。

图4 铁心网格剖分
空载运行时,电枢绕组中没有电流,模型中的电流源只有励磁绕组,且为常数值,通过式(2)算出电流密度加载于励磁绕组区域。利用耦合边界法及静磁分析计算出定转子每单元的磁密信息。图5 显示了在1 / 4 模型中磁场的变化,图5(a)中定转子磁场在公共边界两侧连续,图5(b)中因为耦合节点的偏移,而出现视觉上两侧磁密的不连续。
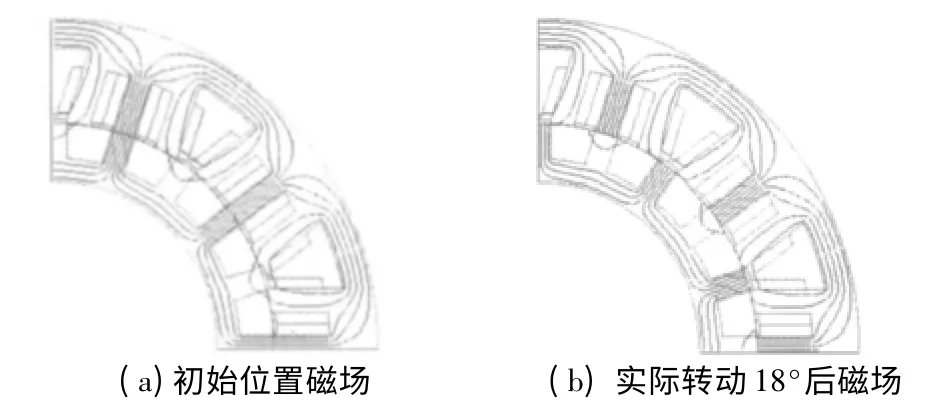
图5 静止模型下的变化磁场
3.3 模型计算与实验验证
为获得电机转速n 下的总铁耗,本文采用间接测量法,即通过总损耗和其他损耗的差值来求解。电机空载运行时,电枢绕组中没有电流,只有励磁绕组铜耗。考虑到励磁绕组的独立性,其输入功耗全部消耗在铜耗上,下面不予考虑。外部电机的转轴输入功率主要消耗在铁耗及机械损耗上:

式中:Pin为励磁状态下外部电机的转轴输入功率,通过转矩转速仪测得;PFe为总铁耗;Pfw为转速n 下的机械损耗,无励磁时转矩转速仪测得的外部机转轴输入功率。
据此空载转速1 100 r/min 时,不同励磁电流下的各损耗如表1 所示。为了使得所测数据更具普遍性,加载了多组励磁电流,使得齿中磁密幅值涵盖了基本磁化曲线的线性段、拐点和饱和部分。其中当励磁电流If为13 A 时,齿中磁密幅值到达基本磁化曲线的拐点。

表1 转速1 100 r/min 时各励磁电流If 下损耗
根据计算所得各单元的磁密幅值及其频率,代入式(11),通过回归分析拟合系数a、b 的线性方程组得出:a = 117.7,b = 466.0。其中计算所得涡流损耗Pte和磁滞损耗Pth在表1 中已列出。
为验证模型的准确性,利用该铁耗模型分别在空载1 800 r/min 和2 200 r/min 下进行了电机铁耗理论值与实测值的对比。图6 显示了2 200 r/min时各励磁电流下的铁耗组成,其中磁滞损耗占据较大的比例。

图6 转速2 200 r/min 时各励磁电流下铁耗
图7 是不同转速下铁耗理论值与实测值的对比,图7 表明铁耗模型在齿中磁密幅值处于磁化曲
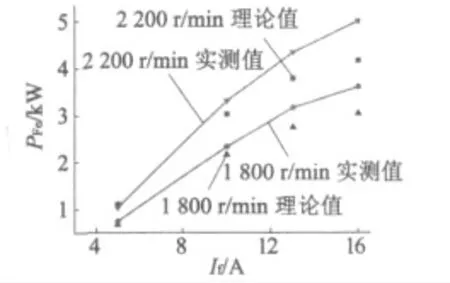
图7 各转速下总损耗理论值与实测值对比
4 结 论
本文对电机旋转状态下磁密及铁耗模型进行了分析,改进了传统铁耗模型,并以一台电励磁双凸极电机为例进行了模型系数的计算和验证,得出以下几点结论:
(1)在电机的磁场模型中,通过耦合边界法处理电机旋转状态下的磁场变化,可以实现用电机静止模型来处理和求解电机旋转过程中的边界及磁场变化问题;
(2)通过获取定转子铁心任意单元的磁密,经过相应的磁密分解以及谐波分析,计算各单元铁耗最后叠加的方法,可以实现总铁耗的求取;
(3)通过对传统铁耗模型的优化和修改,可以直接利用电机的实测铁耗进行模型系数的拟合。本文的铁耗模型系数对应的是DW310-35 硅钢片,该系数适用于该材料铁心的其他电机;此外该模型系数对于预测样机额定负载下的铁耗具有重要意义,并为电机的发热分析奠定了基础。
[1] 陈世坤.电机设计[M].北京:机械工业出版社,2000.
[2] Bertotti G.General properties of power Losses in soft ferromagnetic materials[J].IEEE Trans.on Magnetics,1988,24(1):621-630.
[3] Zhu Jianguo ,Ramsden V S.Improved formulations for rotational core losses in rotating electrical Machines[J].IEEE Trans.on Magnetics,1998,34(4):2234-2242.
[4] Stumberger B,Hamler A,Gorican V,et al.Accuracy of iron loss estimation in induction motors by using different iron loss models[J].Journal of Magnetism and Magnetic Materials,2004:272 -276.
[5] 江善林,邹继斌,徐永向.考虑旋转磁通和趋肤效应的变系数铁耗计算模型[J].电机工程学报,2011,31(3):104-110.
[6] 杨丽,刘闯,严加根.开关磁阻电机铁损的双频法有限元计算研究[J].电机工程学报,2006,26(12):117-121.
[7] 刘晓芳,赵海生,陈伟华.电机铁耗的有限元计算方法研究进展及有待解决的问题[J].电机与控制应用,2010,37(12):1 -6.
[8] 龚余才,潘双来.电路理论基础[M].北京:航空工业出版社,2000:301.线线性段时,理论与计算误差均在10% 以内;即使在磁密饱和情况下,计算误差亦在15% 左右,处于工程设计计算可接受范围以内。
[9] Schuisky W.Berechnung elektrischer maschinen [M].Vienna :Springer-Verlag,1960.
[10] 冯慈璋.电磁场[M].北京:高等教育出版社,1985.
[11] 崔杨,胡虔生,黄允凯.任意频率正弦波条件下铁磁材料损耗计算[J].微电机,2007,40(8):1-3.
