基于振动钻削理论的带压开孔钻具谐响应分析
2012-12-05周立军段梦兰程光明孙晶晶
周立军,段梦兰,2,程光明,孙晶晶
(1.中国石油大学(北京),北京 102249;2.复旦大学,上海 200433)①
近年来,随着海洋输送石油管道损坏事故(主要有机械损伤和内外腐蚀2种形式)的日益增多,相应的海洋管道维修技术的研究也成为海洋石油运输工程中不可或缺的一部分。
带压开孔技术是海洋油气田管道不停产开孔维修方法中的关键环节,开孔质量的好坏将直接决定不停产维修的成败。振动钻削是为了克服普通钻削的自激振动,在钻削刀具上施加某种有规律的、可控的振动,使切削速度等发生周期性的改变,从而改进钻削效果。
谐响应分析[1]是用来分析结构系统由于受持续的周期性载荷所产生相应的周期响应,从而有效防止共振及其他不利振动效果的产生。
海底管道的不停产带压开孔一方面是在海底复杂的环境下进行,另一方面需要一个密闭良好又能保证管道内的流动介质(如油气混合物)不引起灾难事故的环境。振动钻削理论的引入虽然改进了钻削的效果,但由于带压开孔钻具的特殊性以及钻具对振动的反馈作用,致使钻削过程具有一定的不可控性与危险性。因此,对带压开孔钻具进行谐响应分析可以对开孔器具的改进以及钻削过程的相关参数设计提供可靠的理论依据,从而保证带压开孔过程安全有效地进行。
1 带压开孔钻头钻削力理论模型
带压开孔是利用专业的开孔设备(如图1)在需要开孔部位事先预制好法兰短节与之连接,再根据开孔的大小安装相匹配的开孔刀具[2]。
如图1所示,在带压开孔过程中,中心钻首先钻进管道壁层,起到了定位作用,防止振动引起的误差;由于引入了振动钻削,将振动误差转换为外在激励的一部分,因此可以采用无中心钻的钻削方式。
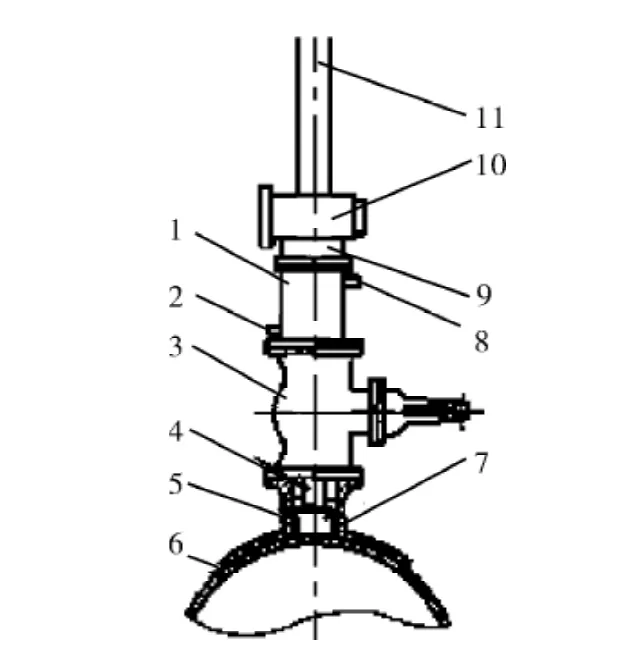
图1 油气管道的带压开孔装置
由于在钻削过程中钻削的宽度和厚度不断地变化,为了便于分析,忽略钻头与刀具形状的影响,将钻头的模型简化为圆柱形,并对其进行离散化。在切削区内将刀具平行划分为无穷小的圆盘形微元,作用在每个微元上的切削力在空间分解为切向力dFt、径向力dFr和轴向力dFa。钻头的切削力模型如图2所示。
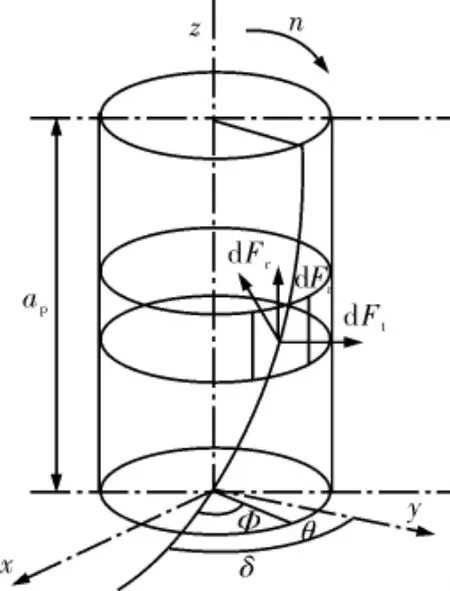
图2 钻头的切削力模型
作用在刀刃微元dz的切向切削力为
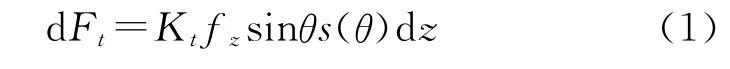
式中,θ为刀具在第i个微元上的瞬时位置角,θ=Φ-δ;Φ为刀具在底部端点的位置角;δ为刀具的滞后角;Kt为切向切削力系数,表示在单位切削深度时单位切削厚度上负载的切削力;fz为每齿进给量;s(θ)为削过程中刀刃与工件的接触窗口函数,刀刃处于钻削区域时s(θ)=1,当刀刃与工件分离时s(θ)=0。
作用在刀刃微元dz的径向切削力为

式中,Kr为径向切削力比例系数。
将切削力变换到xoy坐标系中,则有

式中,g1(θ)=(sin2θ)/2;g2(θ)=(1-cos2θ)/2。
第j个刀齿在刀具转角为Φ时的瞬时切削力为
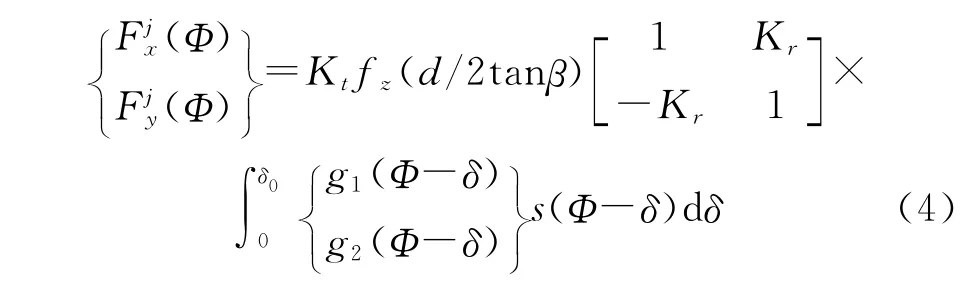
式中,δ0为刀齿在轴向切深ap的滞后角,δ0=aptanβ/(d/2)。
将所有刀齿的切削力相加,得到总切削力为

式中,N 为总刀齿数[3]。
以上是求解普通钻削过程中的切削力,钻具的轴向或周向加入可控的频率振动,形成振动钻削。该方法改变了传统的钻削机理,在加工过程中钻头与工件时切时离,切削力表现为脉冲式的瞬时交变特性,使得钻孔产生的钻削力大幅减小,切削热大为降低,有效地解决了孔加工中钻头刚性不足和切削区难以冷却的问题,尤其降低了带压开孔过程的危险性[4-5]。
振动钻削时,在所加轴向或圆周方向振动的影响下,切削过程中瞬时的实际切削参数都是周期性变化的,并随着振动频率、轴向振幅、主轴转速和进给量fz的不同组合而变化,从而得到间断的或连续的切削过程[6]。
在如图3所示的振动钻削过程中,走刀量为fd=fz+2a0sinwt,w为振动角频率。
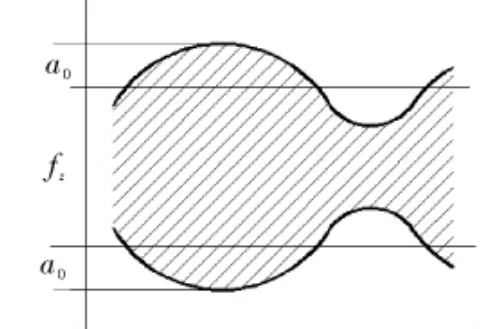
图3 振动钻削的切削断面
根据式(5)中总切削力F与走刀量fz的关系可知,在振动钻削过程中的钻削力F*与钻削走刀量fd的关系式为

2 带压开孔钻杆的振动理论模型
由于带压开孔过程中的严格密闭性与开孔机构的复杂性,使得带压开孔钻具中钻杆的长度远大于其他钻孔作业中所使用的相同型号钻具中钻杆的长度;又鉴于钻削过程中钻削力自身的复杂性与外激振动的引入,使得钻杆的振动成为影响钻削精度的重要因素。为了便于分析钻杆的振动,可以将钻杆的振动模型分为横向振动、轴向振动、扭转振动3种模型进行简化分析[7-12]。
2.1 横向振动模型
根据钻杆的约束及横向的受力状况,将钻杆简化为横臂梁模型,如图4所示。

图4 钻杆的横向振动模型
图4中,Fy(x,t)为振动钻削过程中外激振动下的横向切削力,可由式(6)求得。由图4可得出钻杆横向振动的微分方程为
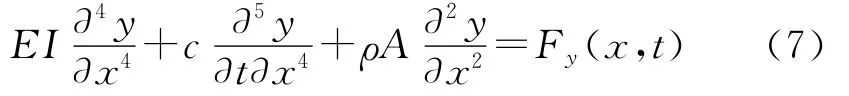
边界条件为
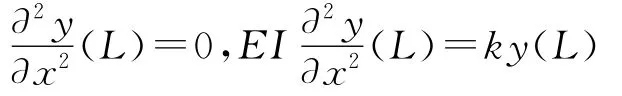
式中,ρ为钻杆的材料密度;EI为弯曲刚度;A为钻杆的横截面积;c为应变内阻尼系数;k为钻杆弯曲角度的正切值;L为钻杆的长度。
2.2 轴向振动模型
忽略其他方向振动的影响,只考虑轴向振动的模型如图5所示。
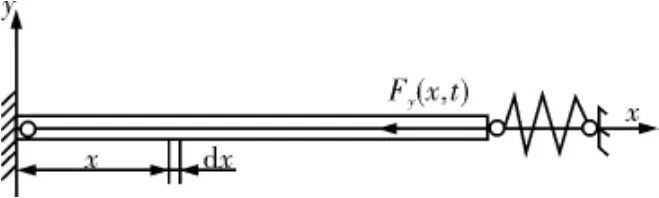
图5 钻杆的轴向振动模型
钻杆横向振动的微分方程为
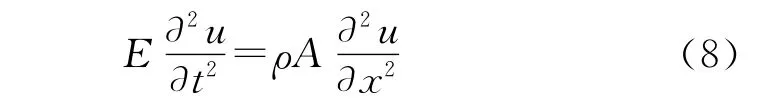
左端边界条件为
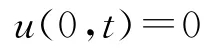
式中,u(x,t)为钻杆横截面在t时刻的位移。
2.3 扭转振动模型
钻杆视为细长均匀圆截面杆,建立其扭转振动模型如图6所示。
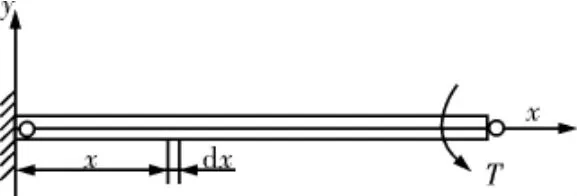
图6 钻杆的扭转振动模型
钻杆的扭转振动模型的微分公式为

左端边界条件为
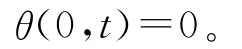
3 带压开孔钻具的谐响应分析
谐响应分析主要用于确定结构在承受周期载荷作用下产生持续的周期响应,以及确定线性结构承受随时间按正弦规律变化的载荷时稳态响应的一种技术,从而能够预测结构的持续动力特性。在带压开孔技术中,对钻具尤其是钻杆的谐响应分析可以得到不同频率、不同振动激励下钻具的响应状态,从而可以选择最佳频率振动,取得良好的切削效果。
实例中,钻杆钻头的材料采用高速钢,其总长度为1.5m;钻削对象是直径为ø711.2mm(28英寸)的海底管道;振动钻削的激励源函数型式为fd=fz+2a0sinwt;激励形式分为横向振动、轴向振动、扭转振动3种形式。
根据管道材料与钻具材料的性质,以及式(6)中所表达的钻削力,将激励源70~180Hz的频率每隔10Hz在Anysys workbench环境下进行谐振动仿真模拟。不同频率下钻具的位移谐响应如图7所示。
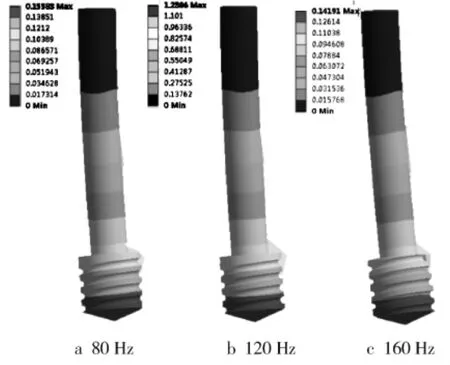
图7 钻具在不同频率外激振动的位移谐响应
由图7可知:钻具的最大位移处发生在钻头顶端,也就是钻具与管道的钻削接触处;位移值的大小从钻头至钻杆末端呈区域性递减,最大位移的关系为Smax(120)>Smax(80)>Smax(160),即最大位移并不是随着频率的增加而增大。在70~180Hz范围内,钻具在120Hz附近达到最大。为便于分析,将100~220Hz之间的钻具谐响应最大位移绘制成曲线,其中110~130Hz之间每隔2Hz取一频率进行仿真,曲线如图8所示。
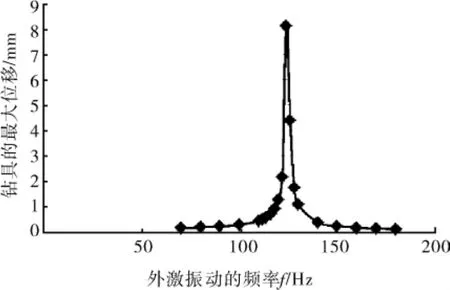
图8 钻具谐响应最大位移与外激频率频率的关系
在分析过程中可以发现:在124Hz附近的外激振动下,钻具钻头达到最大位移时发生突变,甚至发生严重的变形。这说明在124Hz附近,钻具发生共振,采用此频率不但不能改进钻削效果,反而损坏钻具,应当避免。
4 结论
1)带压开孔技术中的振动钻削的钻削力变化是基于外激振动引起的,由于钻削过程的复杂性,横向钻削阻力、轴向钻削阻力以及扭转钻削阻力同时发生周期性的变化,三者相互影响,使得振动钻削不是简单的线性谐响应。
2)钻具的位移响应最大值发生在钻头部位,位移值的大小从钻头至钻杆末端呈区域性递减。在达到共振点附近的区域频率(124Hz)时,钻具发生明显的位移突变,甚至发生严重的变形,采取振动钻削必须避免共振的发生。
;
[1]丁德勇,张 钧,贺双元.推力轴承基座带预应力谐响应分析[J].中国舰船研究,2010,5(3):52-55.
[2]刘 玉,莫建伟.大管径封头带压开孔和封堵技术[J].设备管理与维修,2010(3):23-25.
[3]梁睿君,王宁生,姜澄宇.薄壁零件高速铣削动态切削力[J].南京航空航天大学学报,2008,40(1):89-93.
[4]杜宇波.周向振动钻削切削力分析[J].中国制造业信息化,2009,38(23):82-84.
[5]周 平,赵 军,王云海,等.钻杆带压钻孔机刀杆强度分析[J].石油矿场机械,2011,40(7):51-53.
[6]熊 烽,李淑珍,杜润生,等.振动钻削中切削力的实验研究系统[J].华中理工大学学报,1994,22(9):56-60.
[7]潘小叶,王志红.钻机钻孔时钻杆振动的有限元分析[J].煤矿机械,2009,30(1):92-94.
[8]于桂杰,殷有财,肖文生.顶驱钻井柔性钻柱动力学特性分析[J].石油矿场机械,2011,40(4):1-5.
[9]肖文生,于桂杰.起下钻钻柱纵振理论分析[J].石油矿场机械,2010,39(12):24-26.
[10]崔晓华,周学芹,李玉海.井下钻柱纵向振动特性分析[J].石油矿场机械,2009,38(11):12-15.
[11]赵国山,管志川,王以法,等.钻柱结构声传输特性试验研究[J].石油矿场机械,2009,38(11):45-49.
[12]梅冬琴,刘巨报,李治淼,等.基于加速度传感器的钻柱振动测量方法研究[J].石油矿场机械,2012,41(2):1-7.
