基于多种群分层粒子群优化算法的电力系统低压减载优化方法研究

刘 丽

(成都电业局，四川成都 610021)

0 引言

随着中国国民经济的飞速发展，电网规模不断扩大，逐渐形成了以超特高压电网为骨架、多区域电网互联的新形势。系统的运行状态越来越接近其极限，系统电压崩溃的事故出现频次增多。近些年来，世界范围内的几次电压崩溃事故引起了各国学者对电压崩溃所造成的严重影响和经济损失的重视。快速及时地辨识出系统是否处于紧急状态，并且采取紧急控制措施对防止电压崩溃具有重要意义。电力系统的电压失稳控制措施大多保守且昂贵，自动低压减载装置作为电力系统稳定的重要措施，其有效性和经济性引起了越来越多的关注。

选择合适的安装地点和恰当的控制量可以提高低压减载的效率，对有效实施低压减载，提高系统稳定性至关重要。考虑到传统的低压减载通常根据运行人员经验采用试凑的方法，效率低、安全性差，近年来学者们对最优减载进行了研究。

文献［1］－［6］中，最小切负荷量的计算都是在常规潮流计算框架下进行的，这些方法存在一个严重的不足，即:减载后不能保证系统拥有要求的负荷裕度以及总切负荷量通常较大，不利于系统的经济运行。

首次提出利用多种群分层粒子群优化算法［7］求解低压减载这种非线性混合(离散量和连续量)优化问题的新思路，同时考虑系统电压的稳定裕度，以切负荷量最小为目标函数，避免了利用PSO算法结果易于出现早熟的缺陷，同时提高了优化计算速度，减小了总切负荷量，有利于系统经济运行。在IEEE－39节点系统上的仿真验证了此方法的快速和有效性。

1 低压减载

1.1 低压减载原理

电力系统的电压稳定问题通常发生在重负载情况下元件故障、负荷的突增和重要传输线路的断开。这些扰动都要求系统能够提供足够的无功备用，支撑节点电压，避免系统向电压崩溃点移动。在中国电力系统中，低压减载作为防止电力系统电压崩溃第三道防线中的重要措施有着非常重要的作用［8］，其原理如图1所示。

图1 低压减载原理图

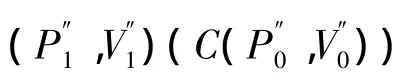
1.2 低压减载数学模型

所考虑电压安全裕度λmin，以切负荷总量最小为目标函数，同时考虑电压安全裕度为潮流约束条件。

目标函数如下。

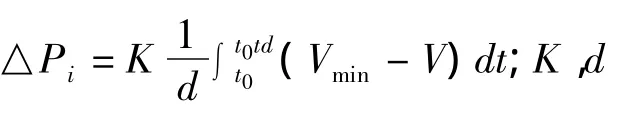
式中，有上标“0”和“C”的分别表示故障前和故障后的相应电气量。NL、lines、NG、ND分别表示节点、线路、发电机、可切负荷点的集合。通过式(2)、(3)、(4)、(5)表明，目标函数在求解过程中既满足静态电压稳定也满足动态电压稳定裕度约束。同时在计算中，假设系统网损由平衡节点提供，发电机的无功输出保持常量。

2 多种群分层粒子群算法

2.1 基本的PSO算法

粒子群优化(particle swarm optimization，PSO)算法最初是由Kennedy和Eberhart博士［9］于1995年受人工生命研究结果启发，在模拟鸟群觅食过程中的迁徙和群集行为时提出的一种基于群体智能的演化计算技术。在该算法中，每个优化问题的解都是D维目标搜索空间中的一个粒子，m个粒子组成一个群体。每个粒子性能的优劣程度取决于待优化问题目标函数确定的适应值，每个粒子由一个速度决定其飞行的方向和速率的大小，粒子们追随当前的最优粒子在解空间中进行搜索［9－10］。假定一个包含m个粒子的粒子群在D维目标空间中搜索，代表潜在问题解的 m 个粒子组成一个种群 S={X1，X2，…，Xi，…，Xm}，其中 X=(xi1，xi2，…，xiD)，表示第 i个粒子在 D维解空间的一个矢量点。将Xi代入一个与求解问题相关的目标函数，即可计算出相应的适应值。用P=(pi1，pi2，…，piD)记录第 i个粒子自身搜索到的最优位置，即适应值为最好，记为pbesti。而在这个种群中至少有一个粒子是最好的，将其编号记为g，则Pg=(pg1，pg2，…，pgD)就是该种群搜索到的最优值(即gbest)，其中g∈{1，2，…，m}，表示搜索到的最优值应该是种群中的某一个粒子。而每个粒子还有一个速度变量，可以用 vi=(vi1，vi2，…，viD)表示第 i个粒子的速度。PSO算法一般采用以下公式对粒子的位置进行更新。

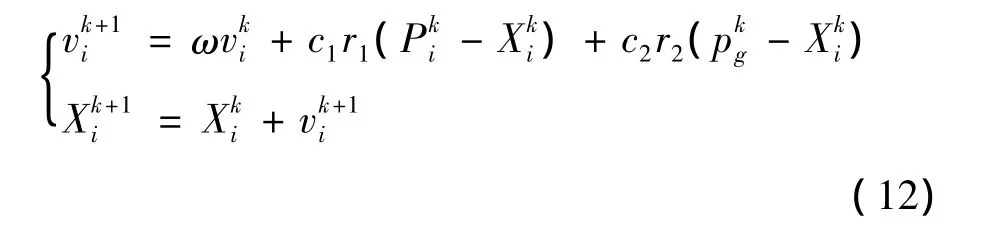
2.2 多种群分层粒子群算法

多种群分层粒子群算法吸取了控制理论的分层思想。在第1层采用多种群粒子群并行计算，等同于增加了粒子个数，扩大了粒子搜索空间范围。在第2层把第1层每个种群看成一个粒子，种群的最优值作为当前粒子的个体最优值，进行第2层粒子群优化，并把优化结果得到的全局最优解反馈到第1层。这样既提高了优化算法的效率，改善了算法的收敛性，同时也使其适用于大规模系统的优化应用［7］。

假设在第1层有L个种群，每个种群有m个粒子，L个种群并行计算，相当于粒子的个数增大为L×m，因粒子数量增多扩大了粒子搜索空间范围。对粒子群进行迭代操作的公式如下。

式中，pig代表第i个种群的全局最优值;pg代表第2层全局最优值;k为迭代次数;w为惯性因子;c1，c2，c3为学习因子;r1，r2，r3为区间［0，1］上的随机数;i代表种群，i=(1，…，L);j代表粒子，j=(1，…，m);xij为第i个种群第j个粒子的位置变量;pij为第i个种群第j个粒子的个体极值。

第2层在第1层多种群粒子群算法的优化基础上再进行2次优化，将L个种群的每个种群看成一个粒子，种群的最优值pij作为当前粒子的个体最优，应用粒子群算法进行第2层寻优。对粒子群算法速度更新进行迭代操作的公式如下。

3 算法实现

运用多种群分层粒子群算法解决低压减载优化问题的算法流程如图2所示。

4 算例分析

以IEEE－39节点系统为例说明上述方法的应用。最后的结果与采用基本粒子群算法(PSO)及遗传算法(GA)的结果比较。同时为了更好地展示低压减载(UVLS)对改善系统电压稳定裕度的积极作用，假设系统在重载条件下运行，即:将系统的负荷值调整为基础值的1.5倍，同时增加发电机输出保证功率平衡。

图1表示系统中电压灵敏度最高的4条母线在正常运行情况下的PV曲线。

可以看出，4条母线的负荷裕度都在允许的范围内，同时具有较大的稳定裕度。

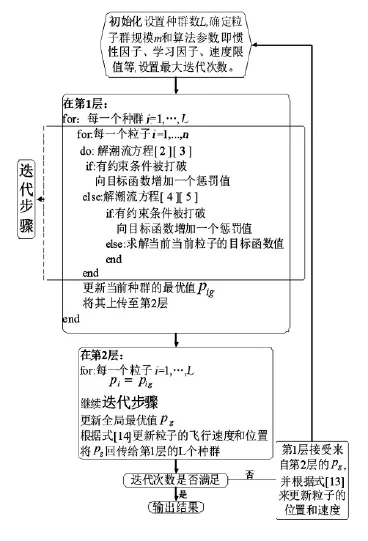
图2 低压减载流程图

此时人为地产生一个扰动，即断开系统中16号和21号节点间的线路，4条母线的PV曲线如图3所示。

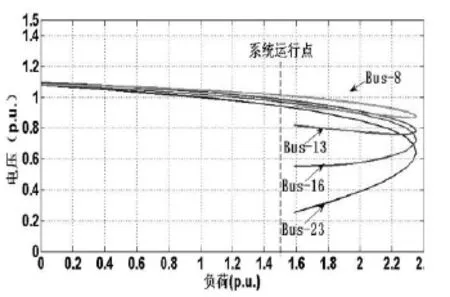
图3 正常运行方式下的PV曲线图

可以看出，4条母线的负荷裕度急剧减小，系统进入紧急状态，为避免系统在新的扰动产生时出现电压崩溃的情况，运用所提方法对系统进行优化减载，其结果与PSO和GA算法比较，结果如表1所示。

表1表明:在同样的裕度和迭代次数要求下，HSPPSO较其他两种算法对UVLS表现出了更好地适应性，以更小的代价满足了要求的电压指标。同时可以看出HSPPSO很好地解决了PSO算法易于陷入局部收敛的缺点，表2表示两种算法在相同的粒子个数和负荷裕度(0.07)要求下，不同迭代次数下总减载量的对比。

图4 16－21号线路断开情况下的PV曲线图

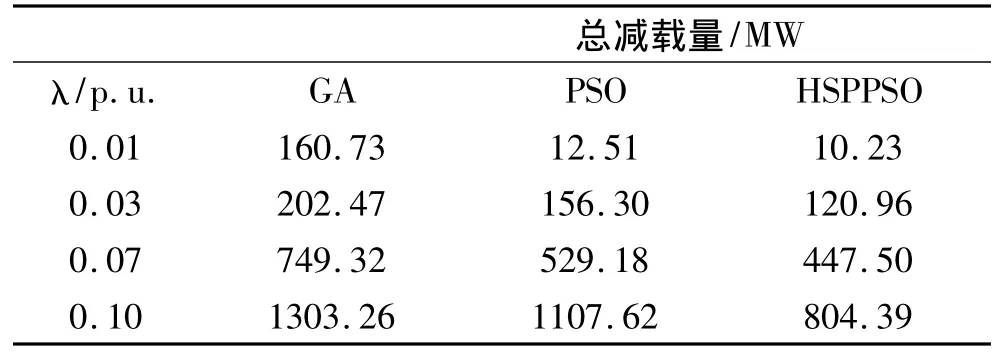
表1 3种算法满足不同裕度时的总减载量

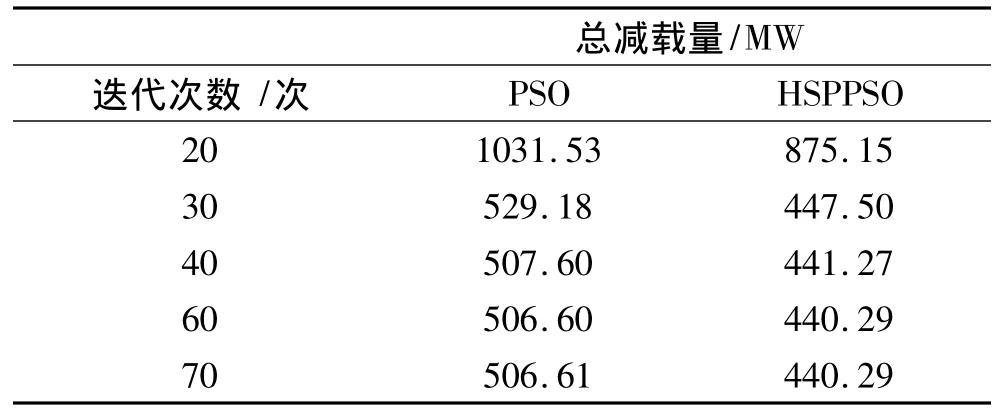
表2 PSO和HSPPSO总减载量比较

通过表2可以看出，在同样的迭代次数下，所应用的HSPPSO较传统的PSO算法表现出了更好的加速收敛效果及精确度。即将分层理论应用于PSO算法改善了该算法收敛速度及早熟的问题。

5 结论

粒子群算法在优化过程中充分发挥了个体和群体的认知、协调能力，是一种全新的智能优化算法，可以解决大规模混合非线性组合优化问题。介绍了电力系统低压减载的基本原理，在考虑系统电压稳定裕度的基础上提出了利用多种群分层粒子群算法(HSPPSO)来解决UVLS这种混合非线性组合优化问题的新思路。在IEEE－39节点系统上的仿真结果表明，所提的方法较PSO和GA算法能够更好地适应所研究的问题，同时HSPPSO有效地解决了PSO算法易于早熟的缺点，为电力系统最优减载提供了新的参考。

［1］刘斌，陈磊，闵勇.考虑暂态电压稳定的低压减载地点选择［J］.电力系统自动化，2008，32(5):11 －14.

［2］TUAN T Q，FANDINO J.Emergency Load Shedding to A-void Risks of Voltage Instability Using Indicators［J］.IEEE Trans on Power Systems，1994，9(1):341 －351.

［3］马平，蔡兴国，于继来，等.基于最小不匹配函数的低压减载算法研究［J］.中国电机工程学报，2005，25(1):27－31.

［4］李碧君，徐泰山，周霞，等.低压减载参数优化整定中暂态电压安全性的考虑［J］.江苏电机工程，2006，25(5):6－8.

［5］Tso S K，Zhu T X，Zeng Q Y，et al.Evaluation of Load Shedding to Prevent Dynamic Voltage Instability Based on Extended fuzzy reasoning［J］.IEE Proc.Gener.Transm.Distrib.，1997，144(2):81 －86.

［6］戴剑锋，朱凌志，周双喜，等.基于风险的低压减载策略问题研究［J］.中国电机工程学报，2006，26(19):18－22.

［7］吕林，罗 绮，刘俊勇，等.一种基于多种群分层的粒子群优化算法［J］.四川大学学报:工程科学版，2008，40(5):171－176.

［8］米增强，田建设，刘力丰.低压减载对电压稳定作用机理的探讨［J］.华北电力大学学报，1999，26(1):31－36.

［9］Kennedy J，Eberhart R.Particle Swarm Optimization［C］.Proceedings of IEEE Conference on Neural Networks，Perth，Australia，1995(4):1942 －1948.

［10］Shi Y，Eberhart R.A Modified Swarm Optimizer［C］.IEEE International Conference of Evolutionary Computation，Anchorage，Alaska，USA，1998.

［11］Clerc M，Kennedy J.The Particle Swarm:Explosion，Stability，and Convergence in Multi－dimension Complex space［J］.IEEE Trans on Evolutionary Computation，2002，16(1):58 －73.

［12］Eberhart R ，Shi Y.Particle Swarm Optimization:development，Applications and Resource［C］.IEEE Int Conf on Evolutionary Computation，Seoul，Korea，2001:81 －86.