基于内模控制的VSC－HVDC风电并网系统控制策略研究

范帅军，凌 颖，赵莉华

(四川大学，四川成都 610065)

0 前言

近年来，轻型直流输电技术(voltage sourced converter HVDC，以下简称VSC－HVDC)作为一种新型输电方式备受关注，它是一种电压源型变换器，以IGBT等全控型器件和脉冲宽度调制(pulse－width modulation，PWM)技术为基础。与传统的交流输电技术和以晶闸管为主控器件的传统高压直流输电技术比较，VSC－HVDC技术具有很多优点，如能够快速并且独立控制系统有功功率和无功功率，灵活改变潮流方向，向交流系统提供紧急无功补偿，易于实现多端直流系统并联，换流站设备小型化和模块化，系统可靠性更高等。所以，VSC－HVDC技术得到了日益广泛的应用，尤其适合于新能源发电系统(如风力发电、燃料电池、光伏发电等分布式电源)的并网、城市配电系统供电、两个交流系统之间的非同步运行，向孤岛系统供电等场合。

在VSC－HVDC系统中，对电压源型变换器的控制是关键，它将直接影响系统的运行性能。目前在VSC－HVDC系统中大多采用较成熟的PID控制技术，这种控制方式实现起来结构简单，但系统需要整定的参数较多，整定复杂，而参数值整定的好坏直接影响控制效果。采用基于内模控制的PID控制方式，在控制器设计时只需要调节一个参数，使参数整定简单快捷，容易实现，同时可以保留双闭环PI控制系统的优良性能，使得系统同时具有良好的鲁棒性和动态响应速度。通过对VSC－HVDC风电并网系统的仿真，结果表明，基于内模控制原理的一个参数整定的VSC－HVDC系统参数保有双闭环PI控制系统的优良性能，系统鲁棒性好，控制精度高，动态响应快。

图1 PID控制系统原理框图

1 内模PID控制基本原理

传统PID控制原理框图如图1所示。图1中，r(t)是系统输入，c(t)是系统输出，u(t)为控制信号，e(t)为系统的误差信息，可知系统传递函数为

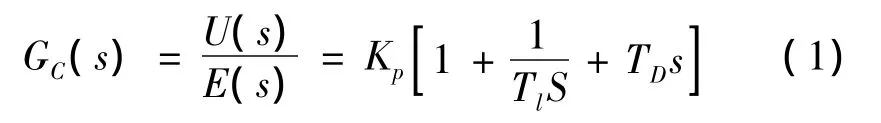
式中，Kp为系统的比例增益;Tl为积分时间常数;TD为微分时间常数。

在PID控制系统中，控制器参数KP、Tl、TD整定的好坏，直接影响控制效果。PID参数的整定有多种方法，这里采用基于内模控制的方法整定控制参数。

图2为内模控制原理框图，图中GC(s)为基于内模控制的PID控制器，它除了包括传统PID控制器Q(s)外，还包括了过程模型pm(s)，而Gp(s)表示被控对象，所以图2中内环的传递函数GC(s)为

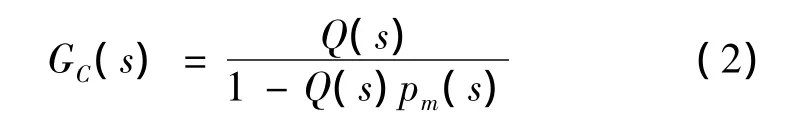
系统闭环响应为

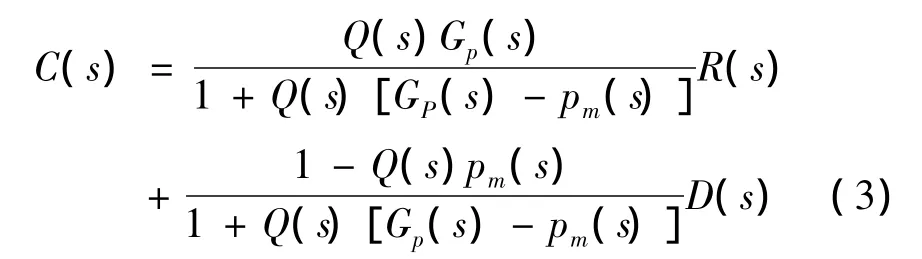
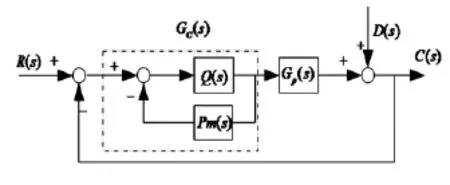
图2 内模PID控制原理框图

将式(3)中的过程模型pm(s)分解为pm+(s)两项和pm－(s)，则有

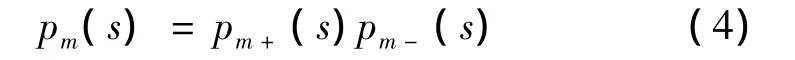
其中，pm+(s)是一个全通滤波器的传递函数，对于所有频率ω，都满足|pm+(jω)|=0，所以pm+(s)包含了内模中所有的时滞环节和右半平面的零点。pm－(s)是具有最小相位特征的传递函数，即稳定且不包含预测项。

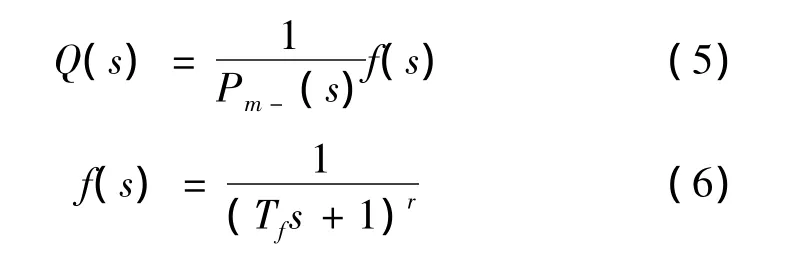
内模PID控制器设计中，最重要的是设计理想内模控制器Q(s)，其设计的主要思想是使Q(s)=P－1m(s)，实际中在不考虑模型失配、约束条件和各种扰动情况下，可使Q(s)→P－1m(s)。为确保系统的稳定性和鲁棒性，在Pm－(s)上增加一滤波器，则内模控制器为f(s)表示静态增益为1的低通滤波器，Tf为滤波器时间常数，其大小决定了系统响应速度。Tf越大，则闭环输出响应越慢，但C(s)对R(s)的跟踪滞后越小，其大小应兼顾动态性能和系统的鲁棒性。参数r为一正整数，取值应保证内模控制器Q(s)有理。|f(s)|的最大幅值为1时，系统有好的鲁棒性能。当r大于1时，f(s)的滤波器能得到更好的输出响应。可知，内模PID控制器只有一个整定参数Tf，Tf的大小同时受系统动态性能与鲁棒性的约束。所以采用内模控制的PID控制器，其参数整定更为简单、便捷。

将式(5)代入式(2)中可以得到内模PID控制器的传递函数为

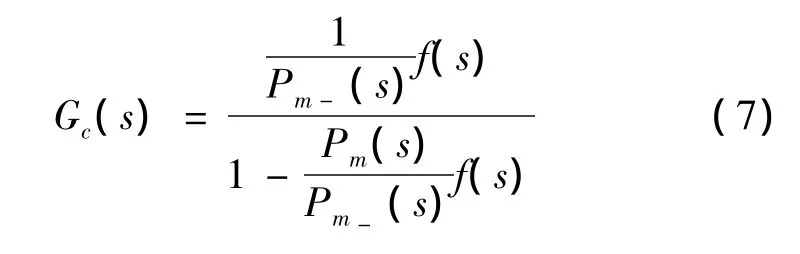
2 基于内模控制的电流控制器设计

VSC－HVDC系统原理图如图3所示，它由两个PWM电压源型换流器、直流传输线路、滤波电容等组成。图中左侧交流系统Es1为交流系统1，右侧交流系统为交流系统Es2为交流系统2，与交流系统1相连的变换器为VSC1，与交流系统2相连的变换器为VSC2;R为换流器电阻;L为换流变压器的电感，它连接换流器与交流系统，同时滤除交流谐波;4个滤波电容C为换流器提供直流侧支撑电压，同时减小直流侧谐波。Es1n、Es2n分别为交流系统1、2的电压，in1和in2为它们的电流;U1n、U2n分别为两个变换器交流侧电压;Udc1、Udc2为两个变换器直流侧电压，is1、is2为两个换流器直流侧电流(这里n=a、b、c)。

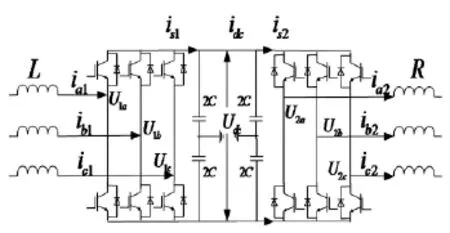
图3 VSC－HVDC系统原理框图

图3中两个变换器及两侧交流系统对称，以交流系统1为例进行讨论。列出交流侧动态微分方程如下。

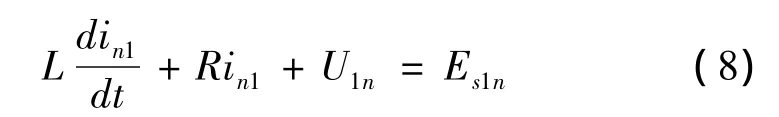
对式(8)进行d、q变换，得到方程组为

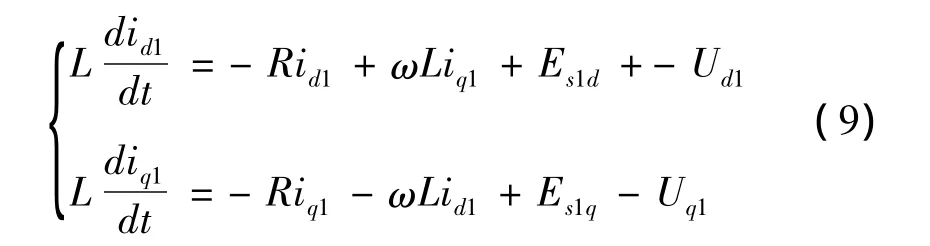
式中，Ud1、Uq1为变换器侧三相交流电压的d轴和q轴分量;Es1d、Es1q为交流系统1三相电压的d轴和q轴分量;id1、iq1为交流系统1的三相电流d轴和q轴分量。从式(9)可知，电流id1、iq1不仅受VSC1侧电压Ud1、Uq1的影响，还受到交流系统1的三相电压Es1d、Es1q和电流交叉耦合项ωLid1、ωLiq1的影响。为了实现对d、q轴的解耦，首先对式(1)采用前馈解耦控制算法，使电压前馈，为了消除d轴、q轴之间的电流耦合和电网电压扰动，令

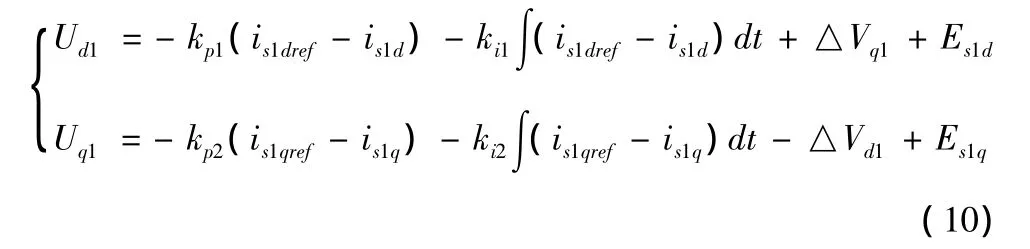
式中，is1dref、is1qref分别为VSC1侧有功电流和无功电流的参考值;kp1、ki1、kp2、ki2分别为 VSC1 内环电流 d、q轴PI控制器的比例积分系数。

于是，由式(9)、(10)得出

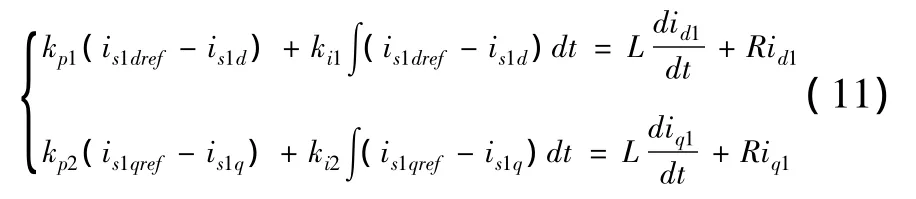
从式(11)可以看出，调节PI参数使之满足式(11)，便可实现内环电流的d、q轴解耦控制，进而实现对Ud1、Uq1的控制。内环电流控制图如图4所示。

由于d、q轴电流各自的控制对象相同，因此控制系统结构和参数可以设置相同，这里仅以d轴电流控制器为例进行设计。

考虑到由于数字化控制带来的控制周期的延迟以及PWM脉冲装置的延迟时间，在控制器中加入一个小时间常数的一阶惯性环节作为信号采样延迟环节，控制框图如图5所示。

图4 内环电流控制框图

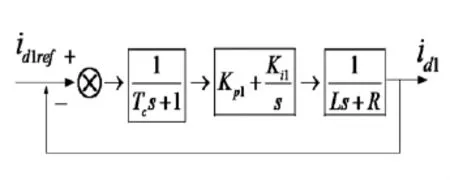
图5 内环电流控制器传递函数等值框图

由于VSC换流器开关频率比较高，可将图5系统进一步简化为图6所示。

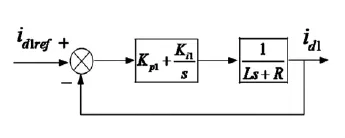
图6 简化后的内环电流控制器传递函数等值框图

即可得出

由此可以看出，对于VSC－HVDC内环电流控制简化的一阶系统而言，采用内模控制原理算法整定PI参数，由公式(13)可知，积分系数kI为固定值，比例系数kp只需由滤波时间参数Tf确定，其大小需折中考虑动态性能和系统的鲁棒性。所以，基于内模原理控制算法来对内环PI参数进行参数整定时，只需调节kp，即只需要整定一个参数即可。

通过对VSC1侧内环电流内模PI控制器和外环直流电压PI控制器的设计，可以得到VSC1系统的定直流电压和定无功功率控制系统结构图如图7所示。

3 系统仿真

对图3所示系统进行仿真，主要仿真参数为:交流系统频率f=50Hz，Es1=Es2=220kV，C=7500μF，R=0.8 Ω ，变压器额定容量 S=200 MVA，直流电压参考值为Udc=100 kV，直流线路长度为70 km的电缆，IGBT开关频率为1 350 Hz。VSC1换流器采用定直流电压控制Udc(pu)=1和定无功功率控制;VSC2换流器采用定有功功率控制p2(pu)=1和定无功功率控制。分别进行了对无功功率控制、潮流反向控制和三相故障的仿真。

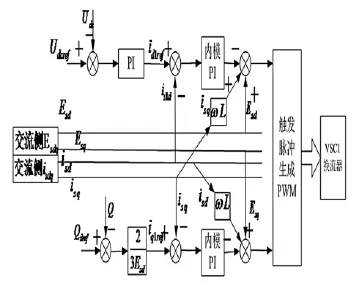
图7 VSC1直流电压、无功功率控制系统结构图

3.1 无功功率控制

仿真的目的是研究当系统送端风力充足全力输出有功而受端处于不同负荷阶段时，两端换流站无功功率流入(流出)的调整情况。送端为定直流电压控制且Udc(pu)=1，受端为定有功控制且P2(pu)=1，VSC1侧输出有功保持恒定。

仿真时，在t=1.5 s时刻，将VSC2侧无功由Q2(pu)=0调整为－0.3;t=2 s时刻，VSC1侧无功由Q1(pu)=0调整为0.3。仿真波形如图8～图11所示。从仿真波形可以看出，对VSC1和VSC2两侧在不同时间进行无功调节，换流器有功输出和直流电压都基本保持恒定，表明系统可根据受端网络和送端网络对无功功率的需求量，在各端灵活调整无功，以达到无功就地平衡的目的。就近补偿无功功率，避免了无功功率远距离传输，减少了网损。而且在受端系统换流站还可以减少对无功设备的投资，不需要根据负荷因数的变化不停地投切无功设备。

3.2 潮流反向

轻型直流输电技术可以通过改变直流电流的方向，瞬时改变有功功率传输方向。

仿真时，t=1.5 s时刻，VSC2侧输入有功从 P(pu)=0.5调整为 －0.5，无功从 Q(pu)=0 调整为－0.2。仿真波形如图13～图17所示，可以看成，轻型直流输电可以通过改变直流电流的方向，来实现有功功率的反向传输，而在系统潮流反向后，功率反向传输非常稳定，直流电压有5%左右的变化。

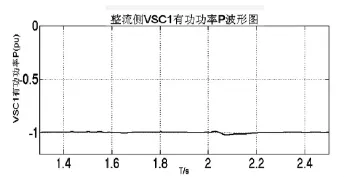
图8 整流侧VSC1有功功率P波形

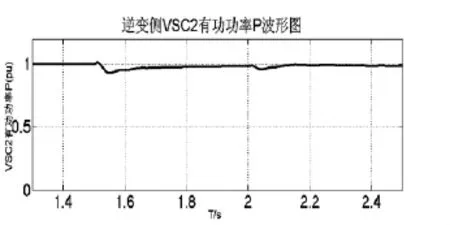
图9 逆变侧VSC2有功功率P波形

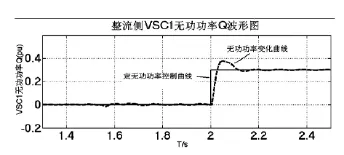
图10 整流侧VSC1无功功率Q波形

图11 逆变侧VSC2无功功率Q波形

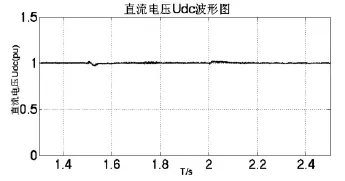
图12 直流电压波形图

3.3 三相故障

在t=1.5 s时，VSC2侧负荷端发生三相短路故障，故障时间为0.1 s。各参考量仿真波形具体见图17～图21。

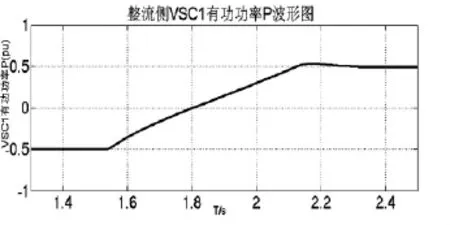
图13 整流侧VSC1有功功率P波形

图14 逆变侧VSC2有功功率P波形

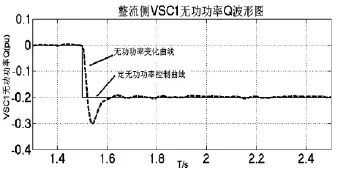
图15 整流侧VSC1无功功率Q波形

图16 直流电压波形

图17 整流侧VSC1有功功率P波形图

VSC2侧负荷端发生三相接地故障，通过对比两侧有功波形及故障侧的电压、电流波形，可以得出VSC2系统故障期间，直流电压出现15%的跌落，当故障切除0.1 s后，直流电压恢复到故障前额定值。同时，VSC2侧的交流电压、有功、无功都降至为0。当故障切除0.1 s后，VSC1、VSC2有功、无功又恢复到故障前的稳定情况。

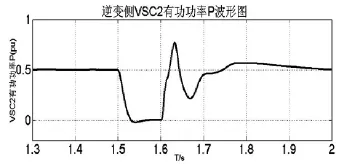
图18 逆变侧VSC2有功功率P波形图

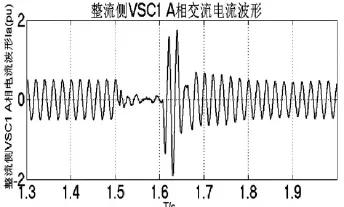
图19 整流侧VSC1 A相交流电流波形

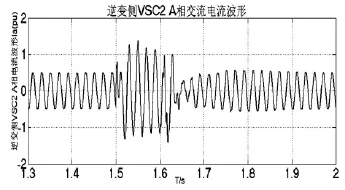
图20 逆变侧VSC2侧A相交流电流波形

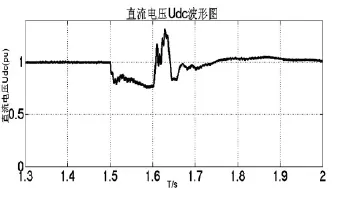
图21 三相故障直流电压波形

4 结论

采用基于内模控制的PID控制算法，克服了传统PI控制中参数多且整定复杂的缺点，在控制器设计时只需要调节一个参数，使参数整定简单快捷，容易实现，同时可以保留双闭环PI控制系统优良性能，使得系统同时具有良好的鲁棒性和动态响应速度。通过对基于内模控制的PI控制构成的VSC－HVDC风电并网系统的仿真，仿真结果表明，基于内模控制原理的一个参数整定的VSC－HVDC系统参数保有双闭环PI控制系统的优良性能，系统鲁棒性好，控制精度高，动态响应快。

［1］刘洋，王钦若.基于内模控制的PID参数整定及仿真［J］.广东工业大学学报，2008，25(1):66－68.

［2］徐应年，赵阳，谌海涛，等.电压源逆变电源输出电压IMC－PID控制技术研究［J］.中国电机工程学报，2007，27(28):90 －95.

［3］Sonali Dasgupta，Gayatri Agnihotri.A Control Strategy of a VSC HVDC System for Power System Enhancement［J］.IEEE Computer Society，2009，6(9):549 －554.

［4］Robinson，G.Joós，VSC －HVDC Transmission and Offshore Grid Design for a Linear Generator Based Wave Farm［J］.2009，1(9):54－58.