Heusler合金Mn2NiAl的电子结构、 磁性质及四方变形的第一性原理

罗礼进, 仲崇贵, 方靖淮, 杨建华, 周朋霞, 江学范

(1. 南通大学 理学院, 江苏 南通 226007; 2. 常熟理工学院 江苏省新型功能材料重点建设实验室, 江苏 常熟 215500)

近年来, 一种兼有温控和磁控的新型形状记忆材料——磁性形状记忆合金(MSMA)已引起人们广泛关注. 磁性形状记忆合金具有受温度控制的热弹性形状记忆效应和受磁场控制的磁性形状记忆效应(MSME). Heusler合金是一种高度有序的三元金属间化合物[1-3], 其中Ni2MnGa[4-6], Ni-Fe-Ga[7-8], Co-Ni-Ga(Al)[9-10], Ni-Mn-In(Sn,Sb)[11]和Mn2NiGa[12]等Heusler合金具有MSME效应.

本文利用基于密度泛函理论的第一性原理方法, 计算Mn2NiAl的晶体结构、 四方变形、 磁性、 电子结构和压力响应等. 计算结果表明, Mn2NiAl在由立方结构向四方结构的变形中出现一个稳定的马氏体相, 且在奥氏体相和马氏体相下均呈亚铁磁结构, 因而Mn2NiAl可能具有MSME效应.

1 计算方法和模型

本文计算利用基于密度泛函理论的投影扩充波函数方法, 即在求解Kohn-Sham方程时, 离子和电子间的相互作用采用投影扩充波函数(PAW)表示, 交换关联能采用广义梯度近似(GGA). 平面波截断能为400 eV,k点网孔用Monkhorst-Pack方法产生, 驰豫和静态计算使用19×19×19个K-网格, 态密度计算使用23×23×23个K-网格, 体系总能的收敛值每个计算单胞取10-4eV. 采用第一性原理计算软件包VASP[13]进行计算.

Mn2NiAl的结构如图1所示. 由图1可见, 该有序结构由A,B,C,D晶位上的原子构成4个fcc子晶格沿体对角线方向相互嵌套而成, 在等效坐标中, A,B,C,D在对角线上的对应坐标分别为(0, 0, 0),(1/4, 1/4, 1/4),(1/2, 1/2, 1/2),(3/4, 3/4, 3/4). 4个子晶格的不同排序可构成2种不同的有序结构: 1) Mn原子占据A和C等效晶位, Ni和Al原子分别占据B和D晶位(称为MnNiMnAl型结构或Cu2MnAl型结构, 如图1(A)所示); 2) Mn原子占据A和B非等效晶位, Ni和Al原子分别占据C和D晶位(称为MnMnNiAl型结构或Hg2CuTi型结构, 如图1(B)所示).

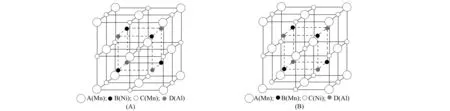
图1 Mn2NiAl的结构Fig.1 Structure of Mn2NiAl

2 结果与讨论

2.1 立方奥氏体相晶体结构的优化

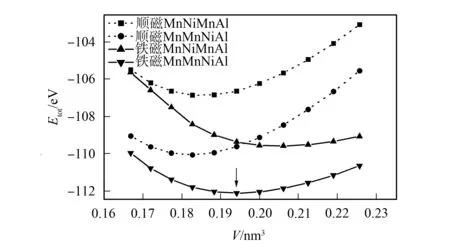
图2 当Mn2NiAl取不同结构和不同磁态时 Etot随晶胞体积的变化曲线Fig.2 Etot as a function of unit cell volumefor MnNiMnAl and MnMnNiAl with different structures and in the different magnetic states

为获得Mn2NiAl在立方奥氏体相的平衡结构, 分别计算当Mn2NiAl取不同结构(MnNiMnAl型结构和MnMnNiAl型结构)和不同磁态(顺磁态和铁磁态)时总能随晶胞体积的变化情况, 如图2所示, 其中“点”为数据点, 曲线为由数据点拟合的曲线. 由图2可见, 在4种情形(顺磁MnNiMnAl、 顺磁MnMnNiAl、 铁磁MnNiMnAl 和铁磁MnMnNiAl)下, 总能(Etot)随晶胞体积的变化呈类似于抛物线变化的趋势, 并存在对应最佳结构的总能最小值. 在晶胞体积变化范围内, 两种结构(MnNiMnAl和MnMnNiAl)的铁磁态均比顺磁态的总能低, 对于两种铁磁态, MnMnNiAl铁磁态的总能最低. 因此可知Mn2NiAl在立方奥氏体相的平衡结构为铁磁态MnMnNiAl型结构, 且立方奥氏体相平衡时的体积为0.194 064 3 nm3(图2中箭头所示), 对应的平衡晶格常数a=0.578 96 nm.

2.2 四方变形及稳定马氏体相的获得

马氏体相可通过改变外加条件(温度、 压力和磁场), 使合金从立方结构形变至一个更低能量的稳定对称结构获得. 为确定Mn2NiAl在四方变形过程中是否存在稳定的马氏体相, 本文计算了Mn2NiAl的总能随形变的变化情况(在铁磁态MnMnNiAl型结构下), 计算过程如下: 1) 体积固定在立方奥氏体相平衡时的体积, 计算Mn2NiAl在四方变形过程中总能随c/a的变化, 计算结果如图3(A)所示. 由图3(A)可见, 在本文讨论的四方变形范围内, 在c/a≈1.24处出现一个能量比立方奥氏体相更低的局域最小值, 表明该处存在一个稳定的马氏体相; 2) 为获得最优的马氏体相结构, 固定c/a=1.24, 计算Mn2NiAl在马氏体相时的总能随晶胞体积的变化情况, 计算结果如图3(B)所示. 由图3(B)可见, 当晶胞体积为0.193 632 9 nm3时(图中箭头所示), 总能取最小值, 对应的结构即为最优的马氏体相结构, 由此可得相应马氏体相的平衡晶格常数a=0.538 92 nm和c=0.666 70 nm. 此外, Mn2NiAl在立方奥氏体相与四方马氏体相的体积基本相等, 表明从奥氏体相相变至马氏体相时的体积基本不变, 该性质为形状记忆合金的一个特性[14].

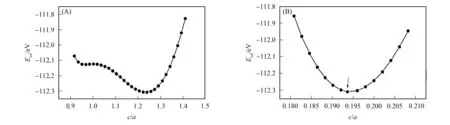
图3 Mn2NiAl在四方变形过程中(体积不变)Etot与c/a的关系(A)和 Mn2NiAl在马氏体相时的Etot随晶胞体积的变化(c/a=1.24)(B)Fig.3 Relationship between Etot and c/a at constant volume for Mn2NiAl in the process of tetragonal distortion (A) and change curve of Etot of Mn2NiAl as a function of the unit cell volume of the tetragonal martensitic phase with c/a=1.24 (B)

2.3 磁 性

为研究Mn2NiAl在奥氏体相和马氏体相的磁性, 本文分别计算了Mn2NiAl在奥氏体相和马氏体相下的总磁矩和各原子自旋磁矩, 结果列于表1. 由表1可见: 在两种状态下, Mn原子对总磁矩的贡献较大, Ni和Al原子对总磁矩的贡献较小; Mn(A)和Mn(B)原子磁矩的值不等且呈反平行耦合, 因而Mn2NiAl合金均呈亚铁磁结构. 在A和B晶位的Mn原子的磁性不同, 这是由于A和B晶位的Mn原子所处的原子环境不同所致, 其中Mn(A)原子最近邻的是4个Al原子和4个Mn(B)原子, Mn(B)原子最近邻的是4个Ni原子和4个Mn(A)原子.

表1 Mn2NiAl在奥氏体相和马氏体相下的总磁矩和各原子自旋磁矩

2.4 态密度

Mn2NiAl在奥氏体相和马氏体相下的总态密度和Mn(A)-d,Mn(B)-d,Ni-d的投影态密度计算结果分别如图4和图5所示. 由图4和图5可见, 在两种状态下, Mn(A)-d和Mn(B)-d的投影态密度分布明显不同. 其中Mn(A)-d的态密度自旋向上部分主要分布在费米能级以上, 自旋向下部分主要分布在费米能级以下. Mn(B)-d与Mn(A)-d的态密度分布相反, 即自旋向上部分主要分布在费米能级以下, 自旋向下部分主要分布在费米能级以上, 因此Mn(A)-d和Mn(B)-d的投影态密度交叠较少. 表明在两种状态下, A和B晶位Mn原子间的d轨道杂化(d-d直接交换作用)均较弱, 而Mn原子内的交换作用较强, 导致两个Mn原子产生较大的自旋劈裂, 形成较大的磁矩. 由于Mn(A)与Mn(B)间的反铁磁耦合由d-d直接交换作用维持, 而Mn(A)与Mn(B)间的铁磁耦合由Al原子的s电子为媒介的间接交换作用维持, 因此Mn2NiAl在两种状态下均呈亚铁磁结构.

图4 Mn2NiAl在奥氏体相下的总态密度 和原子投影态密度Fig.4 Total and atom-projected DOS for Mn2NiAl in austenite

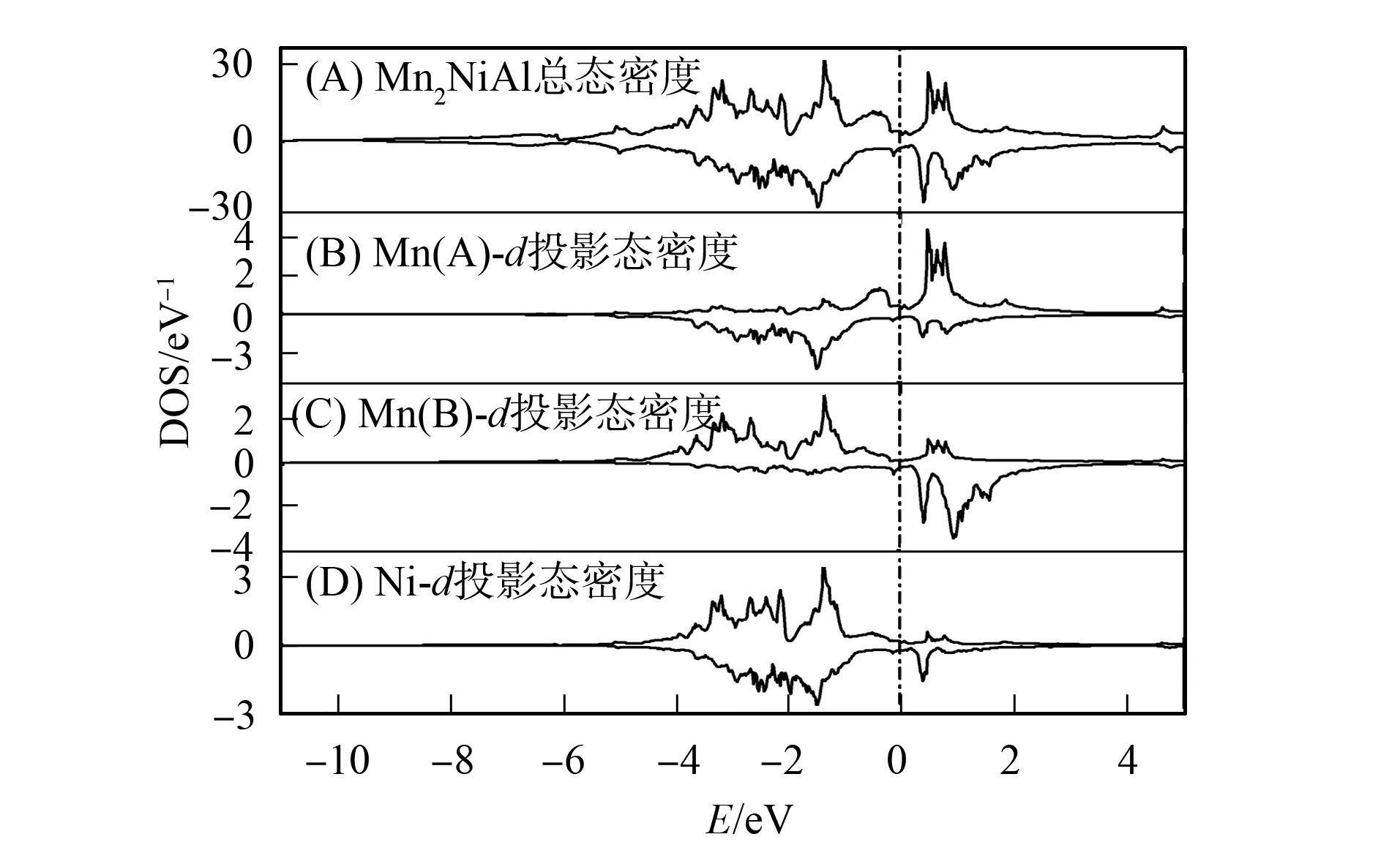
图5 Mn2NiAl在马氏体相下的总态密度 和原子投影态密度Fig.5 Total and atom-projected DOS for Mn2NiAl in martensite

2.5 压力响应

体积弹性模量B可反映物体抵抗弹性变形能力的大小, 定义为

(1)

其中:p和V分别为物体的压强和体积;E为物体的基态总能. 体积弹性模量B0及其对压强导数B′在零压时的值可根据Murnaghan状态方程

(2)

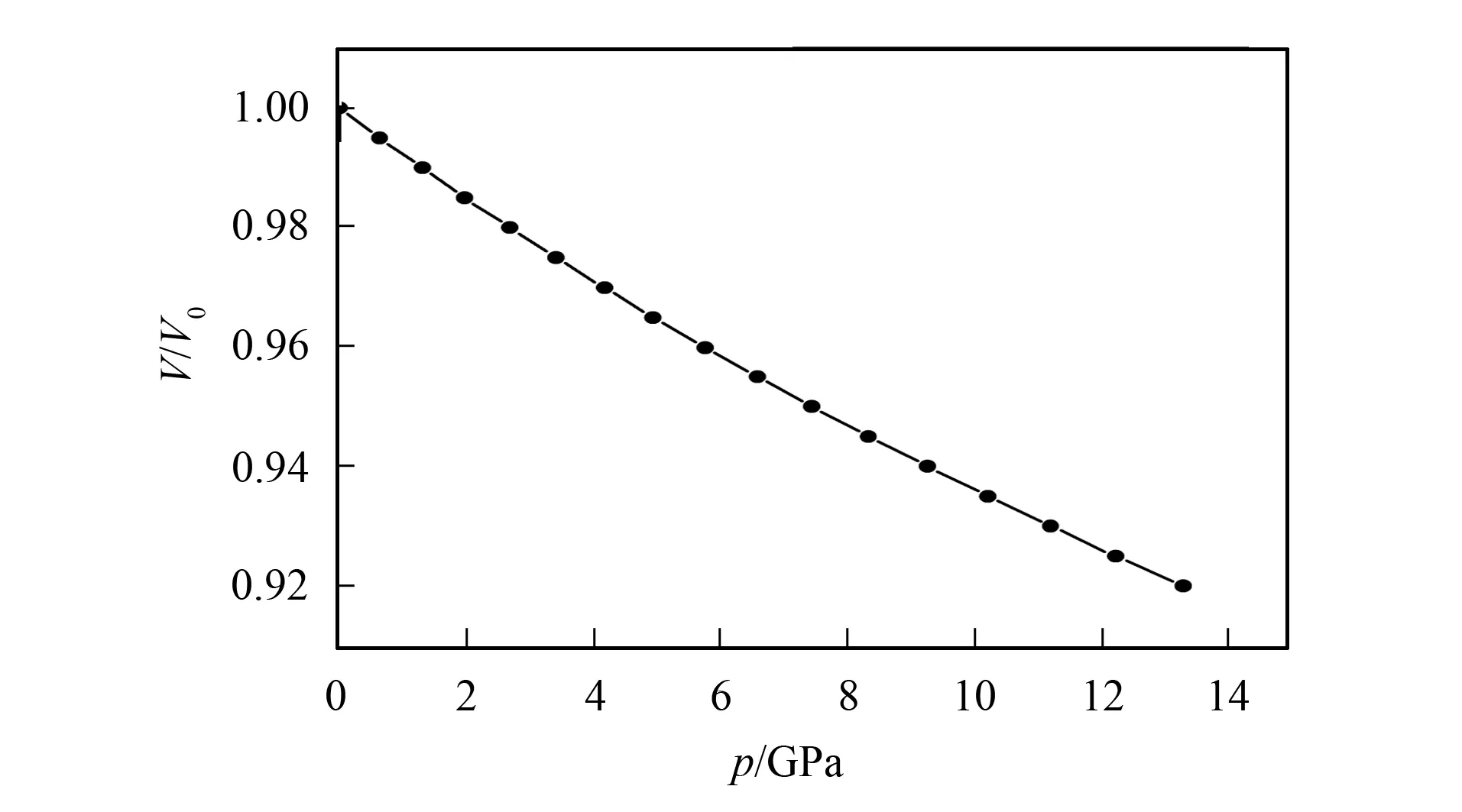
图6 Mn2NiAl的p-V关系Fig.6 p-V relation for Mn2NiAl

进行拟合, 其中V0和E0分别为零压时的体积和总能量. 由式(2)可得

(3)

根据Mn2NiAl的B0=125.69 GPa和B′=5.47, 利用式(3)可得Mn2NiAl的p-V关系曲线, 如图6所示. 由图6可见, 将Mn2NiAl体积(相对于零压时的体积)压缩8%需要的压力约为13.28 GPa. 由Mn2NiAl的零压体积弹性模量B0均小于Ni2MnGe[15], Ni2MnGa[16]和Ni2MnB[17]的零压体积弹性模量可知, Mn2NiAl的抗压缩性均小于Ni2MnGe, Ni2MnGa和Ni2MnB的抗压缩性.

综上, 本文运用基于密度泛函理论的投影扩充波函数方法, 研究了一种新的Heusler合金Mn2NiAl的晶体结构、 四方变形、 磁性、 电子结构和压力响应. 结果表明: Mn2NiAl在立方奥氏体相的平衡结构为铁磁态MnMnNiAl型结构, 平衡晶格常数a=0.578 96 nm; 在由立方结构向四方结构的变形中, 在c/a≈1.24处出现一个能量局域最小值, 表明该处存在一个稳定的马氏体相, 平衡晶格常数a=0.538 92 nm和c=0.666 70 nm; 在奥氏体相和马氏体相下, Mn原子对Mn2NiAl总磁矩的贡献最大, Mn(A)和Mn(B)原子磁矩的值不等且呈反平行耦合, 且Mn(A)-d和Mn(B)-d的投影态密度在费米能级附近交叠均较少, 表明Mn(A)和Mn(B)原子间的d-d直接交换作用均较弱, 而Mn原子内的交换作用较强. 因此Mn2NiAl在奥氏体相和马氏体相下均呈亚铁磁结构. 因此, Mn2NiAl合金可能具有磁性形状记忆效应.

[1] Liu G D, Chen J L, Liu Z H, et al. Martensitic Transformation and Shape Memory Effect in a Ferromagnetic Shape Memory Alloy: Mn2NiGa [J]. Appl Phys Lett, 2005, 87(26): 262504.

[2] LUO Hong-zhi, MENG Fan-bin, FENG Zhong-qiu, et al. The Structural and Magnetic Properties of Mn2-xFexNiGa Heusler Alloys [J]. J Appl Phys, 2010, 107(1): 013905.

[3] XIE Wen-jie, TANG Xin-feng, ZHANG Qing-jie. Fast Preparation and Thermal Transport Property of TiCoSb-Based Half-Heusler Compounds [J]. Chin Phys B, 2007, 16(11): 3549-3552.

[4] Wan J F, Wang J N. Structure Dependence of Optical Spectra of Ferromagnetic Heusler Alloy Ni-Mn-Ga [J]. Physica B, 2005, 355(1/2/3/4): 172-175.

[5] XU Guo-liang, CHEN Jing-dong, CHEN Dong, et al. First-Principles Calculation of Elastic and Thermodynamic Properties of Ni2MnGa Heusler Alloy [J]. Chin Phys B, 2009, 18(2): 744-748.

[6] Jakob G, Elmers H J. Epitaxial Films of the Magnetic Shape Memory Material Ni2MnGa [J]. J Magn Magn Mater, 2007, 310(2): 2779-2781.

[7] Zheng H X, Liu J, Xia M X, et al. Martensitic Transformation of Ni-Fe-Ga-(Co,Ag) Magnetic Shape Memory Alloys [J]. J Alloys Compd, 2005, 387(1/2): 265-268.

[8] Aich S, Das S, Al-Omari I A, et al. Microstructures and Magnetic Properties of Rapidly Solidified Ni54Fe27-2xGa19+2xFerromagnetic Heusler Alloys [J]. J Appl Phys, 2009, 105(7): 07A943.

[9] Tetsuji Saito, Yukihiko Koshimaru, Toshiro Kuji. Structures and Magnetic Properties of Co-Ni-Ga Melt-Spun Ribbons [J]. J Appl Phys, 2008, 103(7): 07B322.

[10] LIU Zhu-hong, YU Shu-yun, YANG Hong, et al. Phase Separation and Magnetic Properties of Co-Ni-Al Ferromagnetic Shape Memory Alloys [J]. Intermetallics, 2008, 16(3): 447-452.

[12] Liu G D, Dai X F, Yu S Y, et al. Physical and Electronic Structure and Magnetism of Mn2NiGa: Experiment and Density-Functional Theory Calculations [J]. Phys Rev B, 2006, 74(5): 054435.

[13] Hafner J. Ab-Initio Simulations of Materials Using VASP: Density-Functional Theory and Beyond [J]. J Comput Chem, 2008, 29(13): 2044-2078.

[14] Aparna Chakrabarti, Barman S R. Theoretical Prediction of Shape Memory Behavior and Ferrimagnetism in Mn2NiIn [J]. Appl Phys Lett, 2009, 94(16): 161908.

[15] Pugaczowa-Michalska M. Electronic Structure, Equilibrium and Magnetic Properties of Ni2MnGe: Ab Initio Study [J]. J Alloys Compd, 2007, 427(1/2): 54-60.

[16] Godlevsky V V, Rabe K M. Soft Tetragonal Distortions in Ferromagnetic Ni2MnGa and Related Materials from First Principles [J]. Phys Rev B, 2001, 63(13): 134407.

[17] Pugaczowa-Michalska M. Electronic and Magnetic Properties and Their Pressure Response in Ni2MnB [J]. J Magn Magn Mater, 2008, 320(16): 2083-2088.