非Lipschitz条件下随机中性技术进步与投资系统解的存在唯一性
2012-12-04严燕,韩笑
严 燕, 韩 笑
(1. 河南财经政法大学 数学与信息科学系, 郑州 450046; 2. 吉林大学 数学学院, 长春 130012)
0 引 言
目前, 关于中性技术进步与投资控制模型的研究已受到人们广泛关注, 并取得了一些研究成果. 文献[1]建立了宏观经济中的投资-生产-再投资过程的发展模型, 得到了资本按使用期发布的变化方程, 并研究了该方程的存在唯一性, 得到了系统稳定的充分条件; 文献[2]讨论了不同中性技术进步下的多要素生产函数, 获得了该类生产函数的一般数学表达式, 并对技术进步做了全新分类; 文献[3]讨论了C-D生产函数和CES生产函数模型, 并针对边界条件用CES生产函数表示的投资控制模型进行了分析, 证明了该投资控制模型解的存在性和唯一性; 文献[4]讨论了中性技术进步条件下的生产函数模型, 即Hicks中性的具有资金服役时间的投资模型, 并证明了该投资模型解的存在唯一性; 文献[5]给出了含有时滞的中性技术进步的资产投资模型, 证明了该投资系统模型的等价方程, 同时得到了等价积分方程的表达式. 但上述讨论只是针对确定系统进行的研究, 而在现实的经济体系中, 中性技术进步与投资系统必然会受随机因素的影响. 因此, 文献[6-7]研究了带有随机因素的中性技术进步与投资系统解的存在唯一性, 并给出了解的指数稳定性. 本文在更一般的条件下证明随机中性技术进步与投资系统解的存在唯一性. 文献[6]中的条件是本文的一种特殊情况.
考虑如下随机中性技术进步与投资系统模型:
(1)
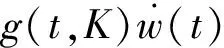
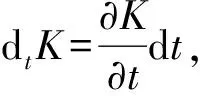
(2)
本文将给出方程(1)解的存在唯一性的基本假设条件, 并证明了解的存在性和唯一性. 本文的一些记号参见文献[6].
假设:
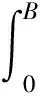

∀x,y∈C, a.e.t,
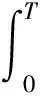
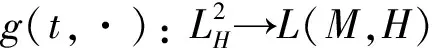
∀x,y∈C, a.e.t;
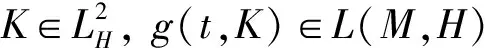
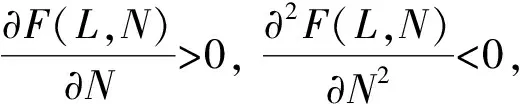
(H5) 存在常数α>0,λ,γ∈R,p>1, 使得下式成立:
∀K∈V, a.e.t.
注1当c(t)为常数且κ(u)=u时, 条件(H2)和(H3)即为文献[6]的假设条件.
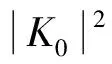
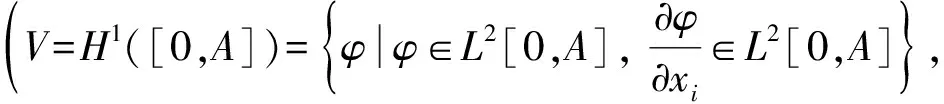
2)Kt∈Ip(0,T;V)∩L2(Ω;C(0,T;H)),p>1,T>0;
3) 对∀t∈[0,T],Kt以概率1满足方程(2).
特别地, 当T=∞时,Kt称为方程(2)的全局强解.
1 解的唯一性和存在性
定理1在假设(H1)~(H4)成立的条件下, 方程(2)的解在Ip(0,T;V)∩L2(Ω;C(0,T;H))上是唯一的.

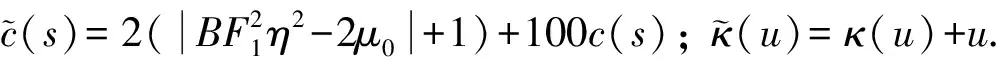
为证明方程(2)解的存在性, 构造迭代序列:
对整数n≥1,
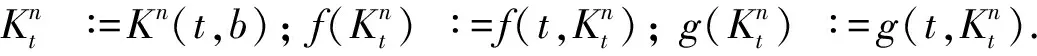


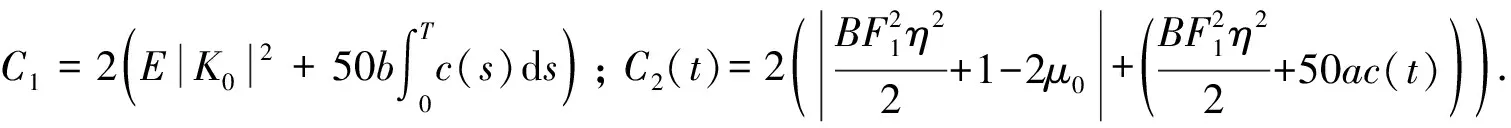


(3)
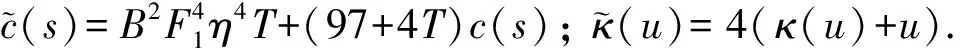

对于∀t∈(0,t1], 定义序列{χn(t)}n≥1如下:
利用数学归纳法可以证明: 对∀t∈(0,t1]及∀m,n>1, 成立
0≤φm,n(t)≤χn(t)≤χn-1(t)≤…≤χ1(t).
(4)
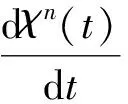



证明: 用文献[8]中引理4相同的证明方法. ∀n≥2, 可得
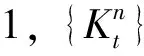
由假设(H5)可得
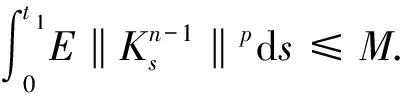
定理2在假设(H1)~(H5)成立的条件下, 方程(2)在Ip(0,T;V)∩L2(Ω;C(0,T;H))上的解存在唯一.

[1] YU Jing-yuan, ZHAO Jun, ZHU Guang-tian. Control Model of Investment about Economic Development [J]. Systems Engineering-Theory & Practice, 1996, 16(4): 13-20. (于景元, 赵军, 朱广田. 经济增长中的投资控制模型 [J]. 系统工程理论与实践, 1996, 16(4): 13-20.)
[2] WANG Sheng-xi, WEN Ping. Generalized Multi-factor Production Functions under the Condition of Neutral Technical Progress [J]. System Engineering-Theory Methodology Applications, 2002, 11(1): 85-88. (王生喜, 文平. 广义中性技术进步下的多要素生产函数 [J]. 系统工程理论方法应用, 2002, 11(1): 85-88.)
[3] LI Hong, WANG Chun, YU Jing-yuan. CES Production Function and Control Model of Investment [J]. Mathematics in Practice and Theory, 2002, 32(3): 438-442. (李红, 王纯, 于景元. CES生产函数与投资控制模型 [J]. 数学的实践与认识, 2002, 32(3): 438-442.)
[4] LI Hong, JIAO Hong-bing, YU Jing-yuan. Neutral Technical Progress and Control Model of Investment [J]. Systems Engineering-Theory & Practice, 2002, 22(7): 47-51. (李红, 焦红兵, 于景元. 中性技术进步与投资控制模型 [J]. 系统工程理论与实践, 2002, 22(7): 47-51.)
[5] XIE Yong-hong, LIU Wen-han, LIU Hui-ru, et al. Properties of the Solution for Investment Model of Neutral Technical Progress Assets with Time Delay [J]. Journal of Hebei Normal University: Natural Science Edition, 2005, 29(2): 116-118. (谢永红, 刘文菡, 刘会茹, 等. 含有时滞中性技术进步的资产投资模型解的性质 [J]. 河北师范大学学报: 自然科学版, 2005, 29(2): 116-118.)
[6] YANG Li-yan, ZHAO Chun. Existence and Uniqueness of Stochastic Neutral Technical Progress and Investment System [J]. Journal of Southwest University for Nationalities: Natural Science Edition, 2007, 33(2): 299-303. (杨丽艳, 赵春. 随机中性技术进步与投资系统解的存在唯一性 [J]. 西南民族大学学报: 自然科学版, 2007, 33(2): 299-303.)
[7] YANG Li-yan, ZHAO Chun, FAN Kuan. The Exponential Stability of the Solution of Stochastic Neutral Technical Progress and Investment System [J]. Journal of Tianjin Normal University: Natural Science Edition, 2007, 27(1): 57-60. (杨丽艳, 赵春, 樊宽. 随机中性技术进步与投资系统解的指数稳定性 [J]. 天津师范大学学报: 自然科学版, 2007, 27(1): 57-60.)
[8] QIN Yan, REN Yong. Existence and Uniqueness for Solutions for Stochastic Age-Dependent Population under Non-Lipschitz Condition [J]. Advances in Systems Science and Applications, 2007, 7(1): 50-59.
[9] LIN Qing-quan. Nonlinear Doob-Mayer Decomposition forg-Supermartingales without Lipschitz Condition ong[J]. Acta Mathematica Scientia: Ser A, 2004, 24(5): 589-596.
[10] Bihari I. A Generalization of a Lemma of Bellman and Its Application to Uniqueness Problem of Differential Equations [J]. Acta Math Acad Sci Hungar, 1956, 7(1): 71-94.
