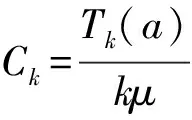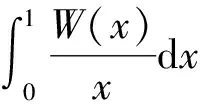截断和乘积的不变原理

周 蕊, 杨金英

(1. 长春理工大学 理学院, 长春 130022; 2. 呼伦贝尔学院 数学科学学院, 内蒙古 海拉尔 021008)

1 预备知识

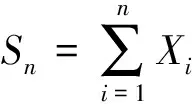
Kn(a)=#{i,Xi∈(Mn-a,Mn]},

从而所有渐近最大值的和为

截断和为

(1)

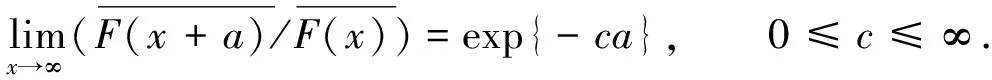
根据c值的不同, 将F分为3类: 当c=0时, 称F具有重尾分布; 当0

定理1[9]设{Xn,n≥1}是独立同分布的正平方可积随机变量序列, 记μ=EX1>0,σ2=VarX1<∞, 变异系数γ=σ/μ, 则

其中N为标准正态随机变量. 文献[10]进一步得到了部分和乘积的不变原理.

定理2[4]设{Xn,n≥1}是独立同分布的正平方可积随机变量序列, 且有连续的中尾分布,μ=EX1>0,σ2=VarX1<∞, 变异系数γ=σ/μ,a为固定的正常数,Tn(a)定义如式(1), 则

P{Tn(a)=0,n=1,2,…的个数有限}=1,

因此可假设Tn(a)处处不为零. 本文在中尾分布的条件下得到了截断和乘积的不变原理.

2 主要结果

设C表示正常数, 不同之处可表示不同的值.

引理1设{Xn,n≥1}是独立同分布的正平方可积随机变量序列, 且有连续的中尾分布,μ=EX1>0,σ2=VarX1<∞. 变异系数γ=σ/μ,a为固定的正常数,Tn(a)定义如式(1), 则在D[0,1]中, 有

(2)

(3)

证明: 式(2)可见文献[6]中引理2.1的证明; 式(3)可见文献[4]中第130页的证明.

定理3设{Xn,n≥1}是独立同分布的正平方可积随机变量序列, 且有连续的中尾分布,μ=EX1>0,σ2=VarX1<∞. 变异系数γ=σ/μ,a为固定的正常数,Tn(a)定义如式(1), 则在D[0,1]中, 有

(4)

其中{W(t),t≥0}为标准布朗运动.

(5)

根据几乎处处收敛的定义知: ∀δ>0, ∃R>0, 使得当s>R时, 有

易知存在子列{δm}0及{Rm}∞, 满足

于是有

显然Am,n<δm. 对于Bm,n, 利用Taylor展式

有

其中θk∈(0,1),k=1,2,…,[nt]. 显然Em,n≤δm. 下面估计Dm,n.

对于任意固定的m, 由式(4), 当n→∞时, 有

(6)

若Rm≥[nt]-1, 则有

(8)

最后证明

(9)

记

H

易证

注意到

而由引理1可知

从而

进一步, 有

于是对于t∈[,1]一致地有

Yn,(t)=H

最后由式(5)～(9)以及文献[11]中的定理4.2可知式(1)成立. 证毕.

所以定理2是定理3中t=1的特例, 因此本文推广了已有的结果.

[1] Pakes A G, Steutel F W. On the Number of Records Near the Maximum [J]. Austral J Statist, 1997, 39(2): 179-192.

[2] Pakes A G, LI Yun. Limit Laws for the Number of Near Maxima via the Poission Approximation [J]. Statist Probab Lett, 1998, 40(4): 395-401.

[3] HU Zhi-shui, SU Chun. Limit Theorems for the Number and Sum of Near Maxima for Medium Tails [J]. Statist Probab Lett, 2003, 63(3): 229-237.

[4] ZOU Hai-lian, ZHANG Li-xin. Asymptotic Distribution of the Product of Trimmed Sums [J]. Journal of Zhejiang University: Science Edition, 2007, 34(2): 128-131. (邹海连, 张立新. 一类截断部分和乘积的渐近正态性 [J]. 浙江大学学报: 理学版, 2007, 34(2): 128-131.)

[5] LIU Wei-dong, LIN Zheng-yan. Some LIL Type Results on the Partial Sums and Trimmed Sums with Multidimensional Indices [J]. Electron Comm Probab, 2007, 12: 221-233.

[6] ZANG Qing-pei, LIN Zheng-yan. The Asymptotic Distribution of the Random Product of Trimmed Sums [J]. J Systems Sci Math Sci, 2009, 29(2): 145-152. (臧庆配, 林正炎. 截断和随机乘积的渐近性质 [J]. 系统科学与数学, 2009, 29(2): 145-152.)

[7] FU Ke-ang, ZHANG Li-xin. A General LIL for Trimmed Sums of Random Fields in Banach Spaces [J]. Acta Math Hungar, 2009, 122(1/2): 91-103.

[8] FU Ke-ang. An Almost Sure Invariance Principle for Trimmed Sums of Random Vectors [J]. Proc Indian Acad Sci Math Sci, 2010, 120(5): 611-618.

[9] Rempala G, Wesolowski J. Asymptotic for Products of Sums and U-Statistics [J]. Electron Comm Probab, 2002, 7(5): 47-54.

[10] ZHANG Li-xin, HUANG Wei. A Note on the Invariance of Principle of the Product of Sums of Random Variables [J]. Electron Comm Probab, 2007, 12: 51-56.

[11] Billingsley P. Convergence of Probability Measures [M]. New York: Wiley, 1968.