求解二次锥规划问题的非精确光滑算法

于桃艳, 刘三阳, 蔡晓娜, 张 菲

(西安电子科技大学 理学院, 西安 710071)

0 引 言

二次锥规划是基于有限个二次锥的笛卡尔乘积的仿射子空间之交上的极小化或极大化线性函数[1]. 本文考虑下列二次锥规划：

(1)

其对偶规划为

(2)

其中:A∈Rm×n;c∈Rn;b∈Rm; 且集合

K={x=(x0,x1)∈R×Rn-1:x0≥‖x1‖}

是一个维数为n的二次锥, ‖·‖表示Euclid范数. 对任意的x=(x1,x2)∈R×Rn-1和s=(s1,s2)∈R×Rn-1,x∘s=(xTs,x1s2+s1x2)∈R×Rn-1. 其中“∘”表示Euclid约当代数中的约当积.

此外, 本文假设问题(1),(2)是严格可行的, 则问题(P)和(D)等价于下列最优性条件：

Ax=b,ATy+s=c,x∘s=0,x∈K,s∈K.

近年来, 二次锥规划问题在许多领域受到广泛关注, 如支持向量机[2]和滤波器设计[3]等, 对于求解该类问题目前已有许多算法, 如内点算法[4]、 非内点连续算法[5]、 无导数下降法[6]和路径跟踪法[7]等. 而对于可行内点算法其要求初始点必须严格可行, 无导数下降法对函数要求较高, 一般要强单调或者单调, 且〈▽xφnew(x,y),▽yφnew(x,y)〉≥0, 而对很多函数计算通常特别复杂, 也很难判断其正负性, 而光滑牛顿算法具有以下优势[8]：

1) 算法对初始点无要求, 不一定要满足可行, 即算法可以从任意点开始;

2) 算法只需解一个线性系统, 且得到唯一搜索方向;

3) 算法可全局收敛到最优解, 且在不需要强互补性的条件下可达到Q-超线性收敛速率.

因为牛顿方程一般不能求出它的精确解, 只能求出它的近似解, 因此文献[9]对于半正定互补问题(SDCP)提出了一种非精确非内点连续算法, 得到了其超线性收敛速率. 基于此, 本文将其应用到二次锥上, 得到了二次锥上的非精确光滑算法. 因为非单调线性策略在实际问题中能提高找到解的可能性及收敛速率, 且能得到较好的数值结果, 故选择步长时引进了非单调线性技术. 最后证明了该算法具有局部二次收敛速率.

1 预备知识

对二次锥上任意向量x=(x1,x2)∈R×Rn-1, 定义其谱分解为x=λ1u1+λ2u2, 其中λi和ui(i=1,2)分别为x的特征值和相应的特征向量, 且

λi=x1+(-1)i+1‖x2‖,

w∈Rn-1是使得‖w‖=1的任意向量. 如果x2≠0, 则上述分解是唯一的.

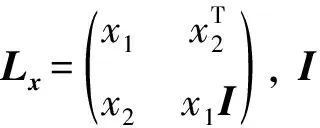
x∘s=Lxs=LxLse,

且Lx为正定(半正定)矩阵当且仅当x∈intK(x∈K), 即x>K0(x≥K0).

2 一类新的光滑函数及其性质

考虑如下Fischer-Burmeister函数[10]:

φFB(x,y)=x+y-(x2+y2)1/2,

满足

φFB(x,y)=0 ⟺x∘y=0,x∈K,y∈K.

由于φFB(x,y)是非光滑的, 因此对φFB(x,y)进行光滑化可得新的向量值函数φ: R×Rn×Rn→Rn, 定义为

(3)

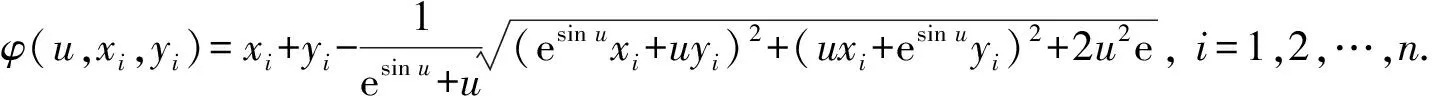
定理11) 函数φ(u,x,y)在任意点Lipschitz连续、 强半光滑且连续可导, 其Jacobi矩阵为

(4)

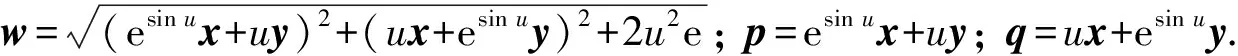
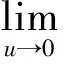
3 非精确光滑算法

本文基于光滑函数(3), 对于大规模的SOCP问题, 提出一种非精确光滑算法. 记z∶=(u,x,c-ATy)∈Rn×Rn×R, 根据光滑函数(3), 定义函数为H: R2n+1→R2n+1为

(5)

令z∶=(u,x,y), Δzk∶=(Δuk,Δxk,Δyk), 在精确光滑算法的每步迭代中, 需求出下面线性方程系统的精确解：

▽H(zk)Δzk=-H(zk),

(6)

其中▽H(zk)为每个迭代点zk的Jacobi矩阵. 由于方程(6)一般只能求出其近似解, 且对于大规模问题即当系数矩阵的维数越来越高时, 求解方程(6)会导致使解的准确性越来越小, 即偏离程度越来越大, 因此为保证精确解在一定的范围内, 需解下列方程系统：

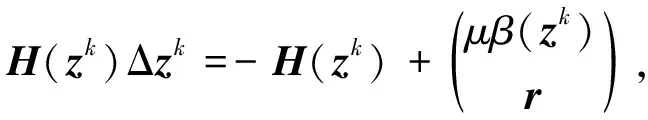
其中:β(zk)=γ‖H(zk)‖min(1,‖H(zk)‖),γ∈(0,1);μ>0是常数, 且满足γμ<1; ‖rk‖=ηk‖H(zk)‖2,ηk∈(0,1),rk为残余向量,ηk为强迫项用于控制精确度.

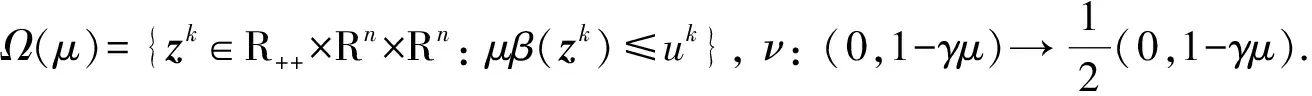
算法1非精确光滑算法.

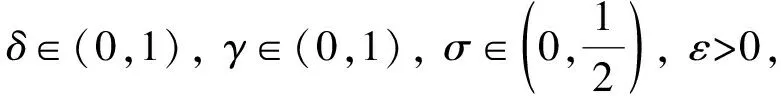
1) 如果‖H(zk)‖≤ε, 则停止, 否则转2);

4) 设zk+1=zk+θkΔzk,ηk+1=v(ηk), 置k=k+1, 转1).

假设1矩阵A是行满秩的.

引理1[8]对任意的x,y∈Rn,w>K0, 有

w2>Kx2+y2⟹Lw-Lx>0,Lw-Ly>0, (Lw-Lx)(Lw-Ly)>0.

定理2设z=(u,x,y)∈R×Rn×Rn,H: R2n+1→R2n+1定义如式(5), 则下列结论成立:

1)H在任意点全局Lipschitz连续、 光滑且连续可微, 且其Jacobi矩阵为

2) 在假设1下, ▽H(z)对任意的u>0是非奇异的, 即算法1中步骤2)是适定的.

证明： 1) 由式(4)可知显然成立.

2) 设Δz∶=(Δu,Δx,Δy), 对任意固定的u>0, 要证▽H(z)是非奇异的等价于▽H(z)Δz=0只有零解, 即判断

(7)

因为

所以由引理1可得

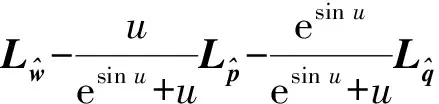
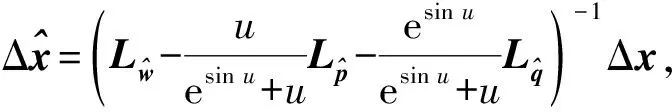
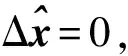
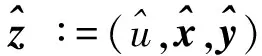
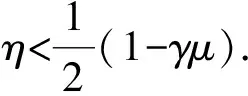
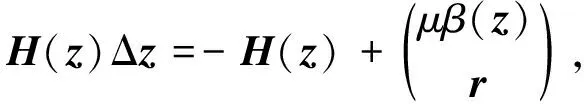
(8)

其中残余向量r满足‖r‖≤η‖H(z)‖, 则由式(8)可得Δu=-u+μβ(z), 从而

u+θΔu=(1-θ)u+θμβ(z)>0.

(9)

定义g(θ)=φ(zk+θΔzk)-φ(zk)-θ(φ′(zk))TΔzk, 则由φ的连续性可得‖g(θ)‖=o(θ), 于是

当‖H(zk)‖>1时,β(zk)=γ‖H(zk)‖min(1,‖H(zk)‖)=γ‖H(zk)‖; 当‖H(zk)‖≤1时,β(zk)=γ‖H(zk)‖min(1,‖H(zk)‖)=γ‖H2(zk)‖≤γ‖H(zk)‖. 故有

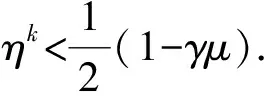
定理4设zk∈Ω(μ), 且zk+1是由算法1产生的序列, 则zk+1∈Ω(μ).

证明： 由zk∈Ω(μ)有uk≥μβ(zk). 由‖H(zk+1)‖≤‖H(zk)‖, 再结合式(9), 分以下两种情形：

1) 当‖H(zk)‖>1时,

β(zk+1)=γ‖H(zk+1)‖min(1,‖H(zk+1)‖)=γ‖H(zk+1)‖≤γ‖H(zk)‖,

2) 当H(zk)≤1时,

β(zk+1)=γ‖H(zk+1)‖2≤γ‖H(zk)‖2,

综上可知, 对任何情况uk+1-μβ(zk+1)≥0都成立, 即zk+1∈Ω(μ).

4 收敛性分析

假设2邻域Ω(μ)是有界的.

引理2设序列{zk}是由算法1得到的, 如果假设2成立, 则序列{zk}的任意聚点都是H(u,x,y)=0的解.

证明类似于文献[9]的定理3.1.

定理5(局部二次收敛性) 序列{zk}是由算法1得到的且收敛到z*, 如果假设2成立, 残余向量序列rk满足‖rk‖=O(‖H(z)‖2), 则序列{zk}局部二次收敛到z*, 即‖zk+1-z*‖=O(‖zk-z*‖2), 且uk+1=O((uk)2).

证明： 由▽H(zk)的非奇异性可知, 对任意的k≥0, ∃C>0, 使得‖▽H(zk)‖≤C. 又因为H(z)是全局Lipschitz连续且强半光滑的, 则当k足够大时, 有

‖H(zk)‖=‖H(zk)-H(z*)‖=O(‖zk-z*‖),

‖H(zk)-H(z*)-▽H(zk)(zk-z*)‖=O(‖zk-z*‖2),

故可得

由于当zk充分接近z*时, 有zk+1=zk+Δzk, 故有‖zk+1-z*‖=O(‖zk-z*‖2).

又因为

uk+1=uk+Δuk=μβ(zk)=μγ‖H(zk)‖2,

(12)

故由式(11),(12)可得

即uk+1=O((uk)2).

综上, 本文给出了一种基于一类新的扰动Fischer-Burmeister函数的二次锥规划非精确光滑算法. 该算法的每步只要求解一个线性系统, 且不要求求出牛顿方程的精确解, 在确定步长的非单调策略下能保证每个迭代点不会远离最优解.当引进的残余向量rk满足‖rk‖=O(‖H(z)‖2)时, 能得到算法的局部二次收敛速率.

[1] Alizadeh F, Goldfarb D. Second-Order Cone Programming [J]. Mathematical Programming, 2003, 95： 3-51.

[2] Debnath R, Muramatsu M, Takahashi H. An Effcient Support Vector Machine Learning Method with Second-Order Cone Programming for Large-Scale Problems [J]. Applied Intelligence, 2005, 23(3)： 219-239.

[3] Shivaswamy P K, Bhattacharyya C, Smola A J. Second Order Cone Programming Approaches for Handling Missing and Uncertain Data [J]. Journal of Machine Learning Research, 2006, 7： 1283-1314.

[4] KUO Yu-ju, Mittelmann H D. Interior Point Methods for Second-Order Cone Programming and OR Applications [J]. Computational Optimization and Applications, 2004, 28(3)： 255-285.

[5] LIANG Fang, HE Guo-ping. A New Non-interior Contimuation Method for Second-Order Cone Programming [J]. International Joint Conference on Computational Sciences and Optimization, 2009, 2： 719-722.

[6] PAN Shao-hua, CHEN Jein-shan. A Linearly Convergent Derivative-Free Descent Method for the Second-Order Cone Complementarity Problem [J]. Optimization, 2010, 59(8)： 1173-1197.

[7] Tsuchiya T. A Polynomial Primal-Dual Path-Following Algorithm for Second-Order Cone Programming [R]. Tokyo: The Institute of Statistical Mathematics, 1997.

[8] Fukushima M, LUO Zhi-quan, Tseng P. Smoothing Functions for Second-Order-Cone Complimentarity Problems [J]. SIAM Journal on Optimization, 2002, 12(2)： 436-460.

[9] RUI Shao-ping, XU Cheng-xian. Inexact Non-interior Continuation Method for Solving Large-Scale Monotone SDCP [J]. Applied Mathematics and Computation, 2009, 215(7)： 2521-2527.

[10] SUN De-feng, SUN Jie. Strong Semismoothness of the Fischer-Burmeister SDC and SOC Complementarity Functions [J]. Mathematical Programming: Ser A, 2005, 103(3)： 575-581.