耦合KdV方程组的格子Boltzmann模型

王慧敏, 刘艳红

(1. 吉林财经大学 应用数学学院, 长春 130117; 2. 吉林大学 数学学院, 长春 130012)

0 引 言

格子Boltzmann方法(lattice Boltzmann method, LBM)是一种起源于格子气自动机(latlice gas automata, LGA)的数值计算方法, 目前已成为用于模拟流体流动的有效工具. 传统的数值方法通常需要求解密度和速度等宏观变量, 而LBM建立在粒子分布函数的细观动力学方程上, 需要求解粒子的分布函数[1]. LBM广泛应用于多相多质流、 粒子悬浮流、 多孔介质流、 磁流体力学、 反应扩散系统及偏微分方程等领域[2-5], 模拟了如波动方程[6-7]、 Korteweg-de Vries(KdV)方程[8-9]、 Burgers方程[10]和Poisson方程[11-12]等.

KdV方程用于描述等离子体物理、 谐晶体和气液混合物中的波现象等, 具有孤波解. 本文使用LBM研究耦合KdV方程组, 该方程组具有如下形式:

(1)

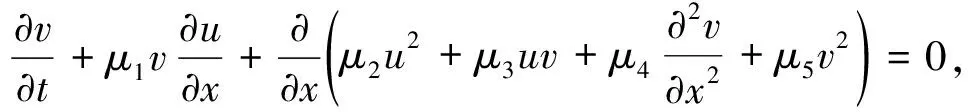
(2)

其中λi和μi(i=1,2,…,5)是任意常数. 当λ1=λ3=0,μ2=μ5=0时, 方程组描述了具有不同色散关系两种长波的相互作用, 并且当μ1+μ3=0时, 两种长波的色散关系在一定条件下, 方程组(1)-(2)有孤波解[13]. 本文为耦合KdV方程组(1)-(2)构建一个格子Boltzmann模型, 并利用该模型对方程组(1)-(2)的孤波解进行数值模拟.

1 格子Boltzmann模型

(3)

(4)

定义Knudsen数ε如下:ε=l/L, 其中:l表示分子的平均自由程;L表示系统的特征尺度. 假设ε与时间步长Δt相等, 则格子Boltzmann方程(4)可以写成：

(5)

将方程(5)左边Taylor展开, 有

(6)

保留至O(ε7)项, 有

(7)

(8)

从而可得如下形式的不同时间尺度上的系列偏微分方程[10]：

(9)

(10)

方程(9)～(14)即为不同时间尺度上的系列偏微分方程, 它们对一维、 二维和三维情况均适用. 在方程(9)～(14)中, 关于弛豫时间因子τ的多项式为：

称为Chapman多项式.

对于一维模型, 定义平衡态分布函数的矩为

其中:

(15)

式(15)中的参数分别为：

(16)

为简便, 本文要求各方向上的源项表达式相同, 即

(17)

由式(9)+式(10)×ε+式(11)×ε2并对α求和, 可得

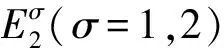
故

对于一维3-bit模型, 有

故

从而式(18)和(19)可化为二阶计算公式：

2 数值模拟

例1

ut+αuxxx+6αuux-6vvx=0,

(27)

vt+βvxxx+3βuvx=0.

(28)

初始条件为

(29)

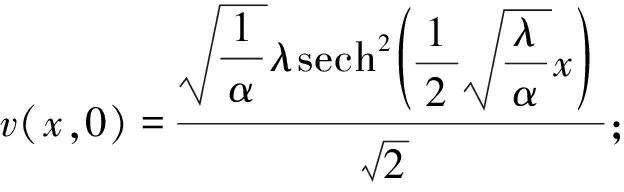
(30)

边界条件为

参数α=β=0.1,λ=0.5,L=5.

数值模拟结果如图1～图6所示, 计算参数为

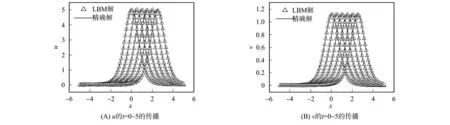
图1 耦合KdV方程组LBM解与精确解的对比结果Fig.1 Comparison results of LBM solution and exact solution of coupled KdV equations

图1为耦合KdV方程组的LBM解和精确解的对比结果. 图2给出了t=1时LBM解的误差(Er)曲线. 图3为u和v从t=0到t=5的对比结果. 图4为误差Er的无穷模和Knudsen数ε的对数关系曲线. 本文还分别使用蛙跳格式和跳点格式对方程组进行数值计算, 图5给出了几种不同数值格式在t=2时的数值解比较结果. 图6为几种不同数值格式当t=2时的误差曲线.

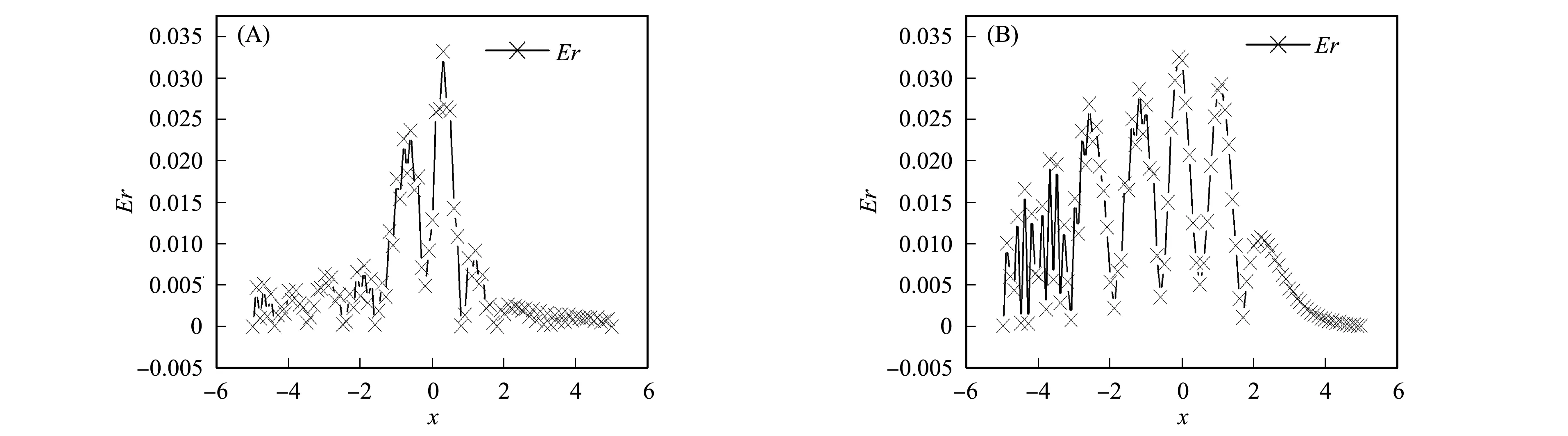
图2 耦合KdV方程组LBM解u(A)和v(B)当t=1时的误差曲线Fig.2 Error curves of LBM solution u(A) and v(B) for coupled KdV equations with t=1

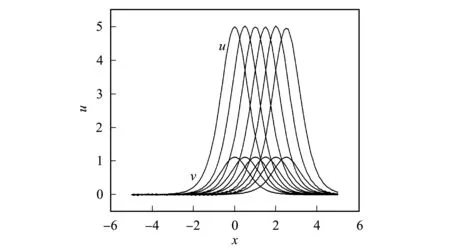
图3 耦合KdV方程组的u和v从t=0 到t=5的对比结果Fig.3 Comparison results of u and v from t=0 to t=5 of coupled KdV equations

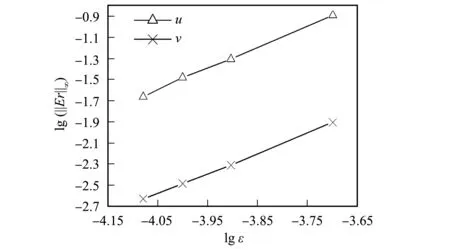
图4 耦合KdV方程组LBM解当t=1时的 ‖Er‖∞和ε的对数关系曲线Fig.4 Logarithmic relationship curves of ‖Er‖∞ vs ε for LBM solution of coupled KdV equations with t=1

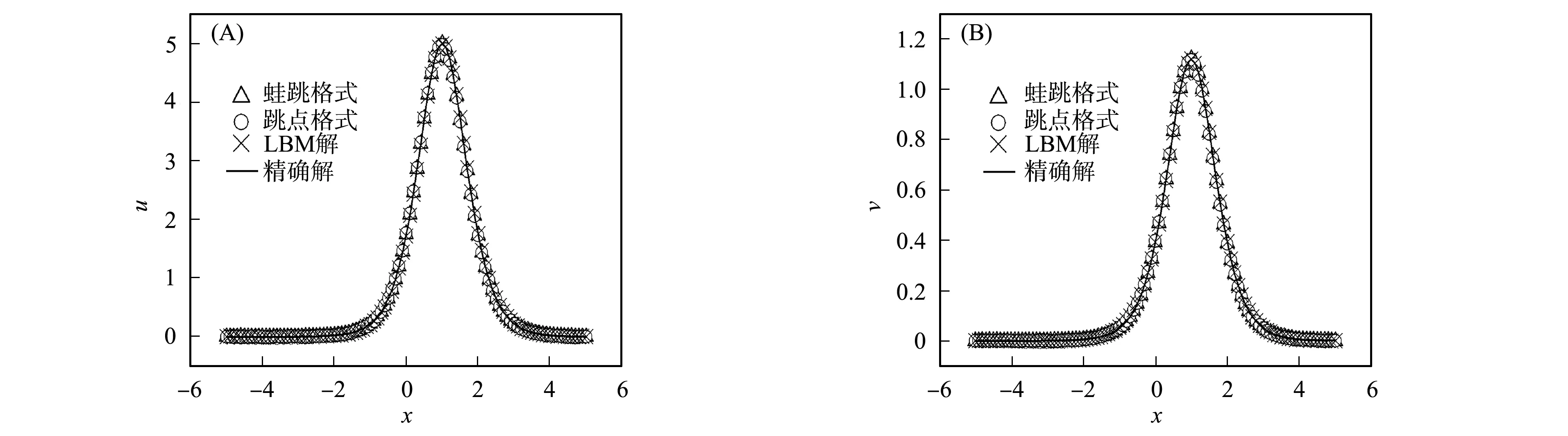
图5 t=2时不同方法数值解u(A)和v(B)的比较结果Fig.5 Comparison results of numerical solution u(A) and v(B) by diffrent methods with t=2

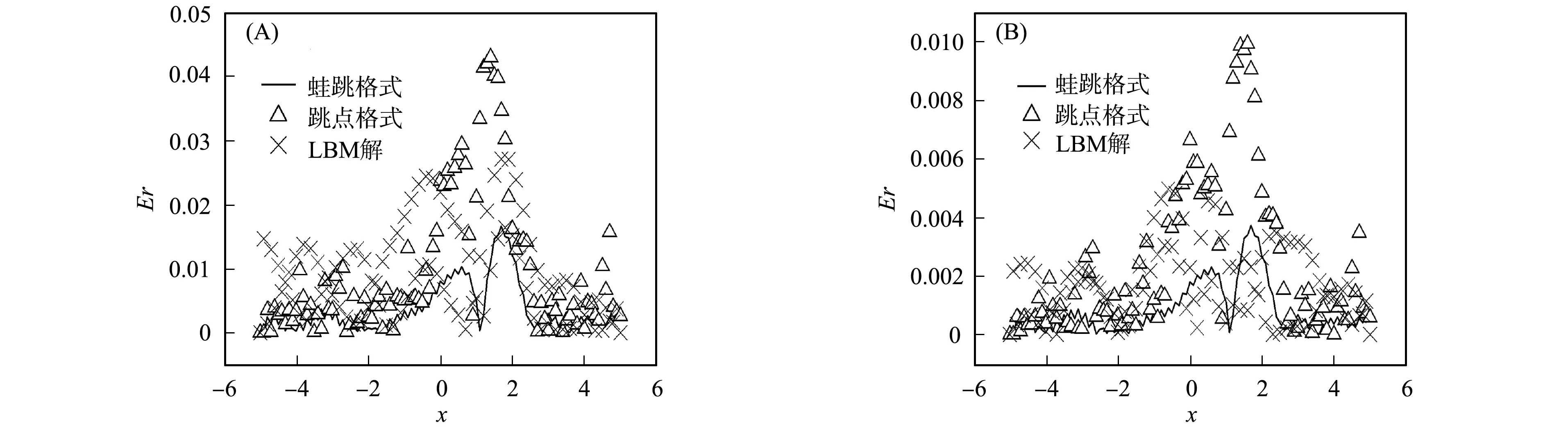
图6 t=2时不同方法的数值误差曲线u(A)和v(B)Fig.6 Numerical error curves u(A) and v(B) by diffrent methods with t=2

由图1～图6可见, LBM的误差介于另外两种数值格式之间. 数值结果表明, 耦合KdV方程组的LBM解与精确解基本一致. 通过与其他传统数值方法进行比较发现, 格子Boltzmann方法与其他数值方法相比计算效果相同, 其模型精度可以接受. 由图4可见, 本文模型的误差对网格数有依赖关系, 网格越密, 模型的误差越小. 数值实验表明, LBM是用于模拟耦合KdV方程组的一种有效方法.

感谢吉林大学数学学院闫广武教授的帮助和指导.

[1] CHEN Shi-yi, Doolen G D. Lattice Boltzmann Method for Fluid Flows [J]. Annu Rev Fluid Mech, 1998, 30: 329-364.

[2] Premnath K N, Abraham J. Three-Dimensional Multi-relaxation Time (MRT) Lattice-Boltzmann Models for Multiphase Flows [J]. J Comput Phys, 2007, 224(2): 539-559.

[3] Holdych D J, Georgiadis J G, Buckius R O. Migration of a Van Der Waals Bubble: Lattice Boltzmann Formulation [J]. Phys Fluids, 2001, 13(4): 817-825.

[4] Mendoza M, Boghosian B M, Herrmann H J, et al. Fast Lattice Boltzmann Solver for Relativistic Hydrodynamics [J]. Phys Rev Lett, 2010, 105(1): 014502.

[5] LUO Li-shi. Theory of the Lattice Boltzmann Method: Lattice Boltzmann Models for Nonideal Gases [J]. Phys Rev E, 2000, 62(4): 4982-4996.

[6] YAN Guang-wu. A Lattice Boltzmann Equation for Waves [J]. J Comput Phys, 2000, 161(1): 61-69.

[7] ZHANG Jian-ying, YAN Guang-wu, SHI Xiu-bo. Lattice Boltzmann Model for Wave Propagation [J]. Phys Rev E, 2009, 80(2): 026706.

[8] YAN Guang-wu, ZHANG Jian-ying. A Higher-Order Moment Method of the Lattice Boltzmann Model for the Korteweg-de Vries Equation [J]. Mathematics and Computers in Simulation, 2009, 79(5): 1554-1565.

[9] ZHANG Jian-ying, YAN Guang-wu. A Lattice Boltzmann Model for the Korteweg-de Vries Equation with Two Conservation Laws [J]. Comput Phys Commun, 2009, 180(7): 1054-1062.

[10] ZHANG Jian-ying, YAN Guang-wu. Lattice Boltzmann Method for One and Two-Dimensional Burgers Equation [J]. Physica A, 2008, 387(19/20): 4771-4786.

[11] WANG Hui-min, YAN Guang-wu, YAN Bo. Lattice Boltzmann Model Based on the Rebuilding-Divergency Method for the Laplace Equation and the Poisson Equation [J]. J Sci Comput, 2011, 46(3): 470-484.

[12] CHAI Zhen-hua, SHI Bao-chang. A Novel Lattice Boltzmann Model for the Poisson Equation [J]. Appl Math Modell, 2008, 32(10): 2050-2058.

[13] LIU Xi-qiang, BAI Cheng-lin. New Soliton Solutions of the Couple KdV Equations [J]. Chinese Journal of Quantum Electronics, 1999, 16(4): 360-364. (刘希强, 白成林. 耦合KdV方程的新孤子解 [J]. 量子电子学报, 1999, 16(4)： 360-364.)