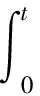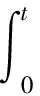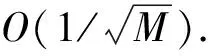一类线性随机Volterra积分方程的数值方法
2012-12-04赵文举
王 秀, 张 稳, 赵文举
(吉林大学 数学学院, 长春 130012)
0 引 言
随机Volterra积分方程在金融数学[1]和生物科学[2]等领域被用来描述客观现象. 目前关于Volterra积分方程的研究多数考虑其确定问题, 包括正则核[3-4]和奇性核[5]等. Atkinson等[6]使用离散配置法求解了非线性Volterra积分方程; Elnagar等[7]利用Chebyshev谱方法求解了Volterra-Hammerstein积分方程. 但对于带随机项的Volterra积分方程目前研究结果不多[8]. 本文主要针对一类线性随机Volterra积分方程, 证明其解的存在性和唯一性, 并给出了相应配置法和收敛性结果.
考虑如下线性随机Volterra积分方程:
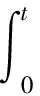
(1)
其中K: [0,T]×[0,T]→R,σ: [0,T]→R,g: [0,T]→R都是连续函数.
1 主要结果
首先, 利用压缩映射原理[9]证明方程(1)解的存在性和唯一性. 给定概率空间(Ω,F,P), 定义空间
易知它是一个完备空间[10]. 对任意的X(t) ∶=X(t,ω)∈L2([0,T]×Ω), 定义算子:
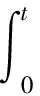
则T是L2([0,T]×Ω)→L2([0,T]×Ω)的算子, 而且X(t)是方程(1)的解当且仅当X(t)是算子T的不动点.
定理1对于给定的概率空间(Ω,F,P)和Wiener过程{Wt,t∈[0,T]}, 若K∈C([0,T]×[0,T]),σ∈C([0,T]),g∈C([0,T]), 则随机Volterra积分方程(1)存在解X∈L2([0,T]×Ω).
证明: 定义迭代序列
(2)
其中: 0≤s≤t≤T;k=0,1,…. 往证X(k)∈L2([0,T]×Ω),k=0,1,….
利用数学归纳法. 因为g∈C([0,T]),K∈C([0,T]×[0,T]),σ∈C([0,T]), 故存在正数M1,M2,M3, 使得
g(t)≤M1,K(t,s)≤M2,σ(t)≤M3, ∀0≤s≤t≤T,

假设对于某个k,X(k)(t)∈L2([0,T]×Ω), 则由式(2)、 Cauchy不等式和It恒等式, 有
即X(k+1)∈L2([0,T]×Ω).

d(k)(t)≤Mk+1tk+1/(k+1)!,k=0,1,…, 0≤t≤T.
(3)
当k=0时, 有

假设对某个k-1, 有dk-1(t)≤Mktk/k!, 则
式(3)得证.
利用鞅不等式[11]及式(3), 有
进一步, 利用切比雪夫不等式[11], 可得
所以
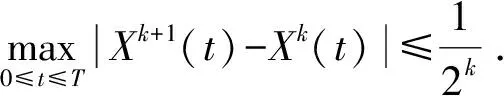
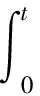
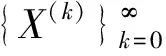
定理2对给定的概率空间(Ω,F,P)和Wiener过程{Wt,t∈[0,T]}, 若K∈C([0,T]×[0,T]),σ∈C([0,T]),g∈C([0,T]), 则随机Volterra积分方程(1)的解唯一.
证明: 假设X1和X2都是方程(1)的解, 则对于所有的0≤t≤T, 有
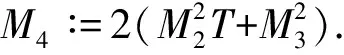
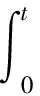
由Gronwall引理[12]知φ=0, 即X1(t)=X2(t) a.s., ∀0≤t≤T. 证毕.
基于实际工程及虚拟装置的直流输电控制保护模型设计方法//柏传军,叶周,程璐璐,肖建民//(14):186

其中P1表示次数不超过1的多项式. 在区间[tn-1,tn)(n=1,2,…,N)上, 取配置点为c1,c2, 并定义
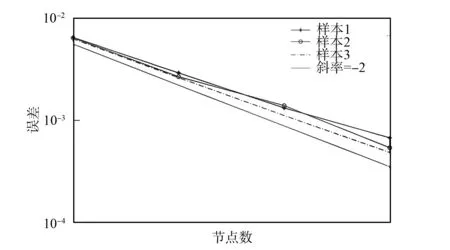
Xh∶={tni=tn+cih: 0=c1 则相应的第m(m=1,2,…,M)个样本插值逼近为 于是, 样本X(m)(t)在[0,T]上可用配置解 (5) 逼近. 将式(5)代入方程(1)中, 可以得到样本近似解满足方程 相应的配置格式为 (6) (7) (8) 利用确定问题的配置法收敛性[3]和Monte-Carlo方法的收敛性, 有 (9) 其中: ‖·‖∞为关于时间t的最大模;C为与网格无关的常数. 下面通过两个数值实验验证定理3给出的收敛性结果. 例1考虑如下随机Volterra积分方程: (10) 其中g(t)=4et+3t-4. 方程(10)的解为E(X(t))=2et-2cost+5sint. 选取h=1/N为步长做一致剖分, 则tn=nh(n=1,2,…N), 且在区间[tn-1,tn)内取tn1=nh,tn2=(n+1/2)h作为配置点. 为验证定理3的收敛性, 先分别取3组样本M=106, 然后依次取N=10,20,40,80, 计算误差 例2考虑如下随机Volterra积分方程: (11) 表1 例1的误差 表2 例2的误差 图1 例1的收敛阶Fig.1 Plot of example 1’s covergence order 图2 例2的收敛阶Fig.2 Plot of example 2’s covergence order [1] Kwok Y K. Mathematical Models of Financial Derivatives [M]. 2nd ed. New York: Springer, 2009. [2] Israel G. Book on Mathematical Biology [M]. Amsterdam: Elsevier, 2005. [3] Brunner H. Collocation Methods for Volterra Integral and Related Functional Differential Equations [M]. Cambridge: Cambridge University Press, 2004. [4] Brunner H, XIE He-hu, ZHANG Ran. Analysis of Collocation Solutions for a Class of Functional Equations with Vanishing Delays [J]. IMA J Numer Anal, 2011, 31(2): 698-718. [5] CHEN Yan-ping, TANG Tao. Convergence Analysis of the Jacobi Spectral-Collocation Methods for Volterra Integral Equations with a Weakly Singular Kernel [J]. Math Comp, 2010, 79: 147-167. [6] Atkinson K, Flores J. The Discrete Collocation Method for Nonlinear Integral Equations [J]. IMA J Numer Anal, 1993, 13(2): 195-213. [7] Elnagar G N, Kazemi M. Chebyshev Spectral Solution of Nonlinear Volterra-Hammerstein Integral Equations [J]. J Comput Appl Math, 1996, 76(1/2): 147-158. [8] ZHANG Xi-cheng. Euler Schemes and Large Deviations for Stochastic Volterra Equations with Singular Kernels [J]. J of Differential Equation, 2008, 244(9): 2226-2250. [9] 江泽坚, 孙善利. 泛函分析 [M]. 北京: 高等教育出版社, 2005. [10] Berger M, Mizel V. Volterra Equations with ItIntegrals, Ⅰ and Ⅱ [J]. J Integral Equations, 1980, 2: 187-245; 319-337. [11] Lawrence C E. An Introduction to Stochastic Differential Equations [M]. 2nd ed. UC: Berkeley, 2002. [12] 黄明游, 冯果忱. 数值分析 [M]. 北京: 高等教育出版社, 2007.

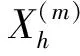
2 数值例子