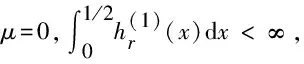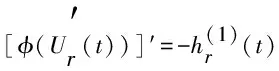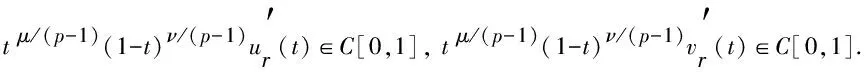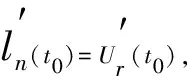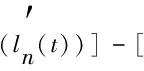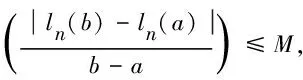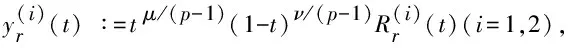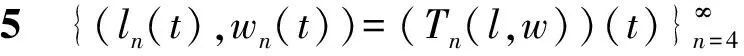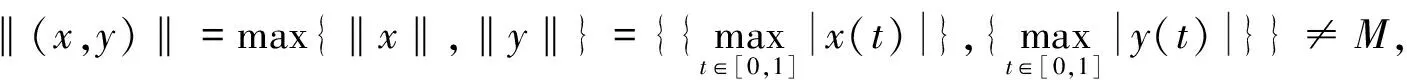二阶p-Laplacian方程组奇异边值问题解的存在性

胡卫敏, 蒋达清

(1. 伊犁师范学院 数学与统计学院应用数学研究所, 新疆 伊宁 835000; 2. 东北师范大学 数学与统计学院, 长春 130024)

0 引 言

考虑如下奇异边值问题:

(1)

目前, 关于边值问题

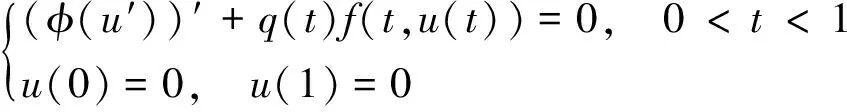
(2)

的研究已有许多结果[1-15]. 文献[5-8]给出了问题(2)当非线性项不具有奇性时的存在性结果; 文献[1,9]给出了当p=2时奇异边值问题(奇性依赖于变量)的一些存在性原则; 文献[10]研究了当p=2 时离散边值问题解的存在性; 文献[11]研究了当p=2时连续边值问题解的存在性. 而关于二阶p-Laplacian方程组奇异边值问题解的存在性研究目前文献报道较少.

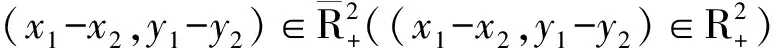
若奇异边值问题(1)满足以下条件, 则称(x(t),y(t))是问题(1)的正解:

1) (x,y)∈C[0,1]×C[0,1]∩C1(0,1)×C1(0,1);

2) ∀t∈(0,1), (x,y)>(0,0), 且x(0)=y(0)=A,x(1)=y(1)=B;

3)φ(x′(t)),φ(y′(t))在(0,1)中绝对连续, 且满足:

1 存在性原则

假设条件:

(H1)fi(t,x,y)∈C((0,1)×R2,R)(i=1,2);

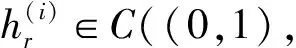
(3)

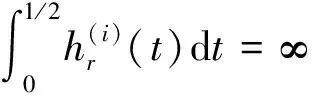
(4)

(5)

注2容易验证条件(H2)蕴含着

其中φ-1(t)是φ(t)的反函数. 事实上,

类似地, 有

引理1边值问题

(6)

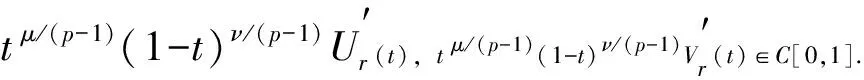
证明: 由于唯一性的证明很简单, 这里只证明存在性. 对任意的0

由注2, 显然y(t)在(0,1)中连续非增且y(0+)<0

取

(7)

则Ur是定义在(0,1)上的函数, 且有

(8)

对于0

类似地有, 当0<ν

因此,Ur(t)在[0,1]上连续,

同理, 若取

也有类似结论.

类似引理1的证明, 有:

引理2边值问题

对每个固定的(x,y)∈D, 考虑如下边值问题:

(9)

先考虑修正后的边值问题:

(10)n

其中:n≥4是自然数;ηn(t)在[0,1]上连续, 且满足0≤ηn(t)≤1及

(12)n

和

(13)n

引理3令(ln(t),wn(t))是问题(10)n的解, 则

(ur(t),vr(t))≤(ln(t),wn(t))=(Tn(l,w))(t)≤(Ur(t),Vr(t)), 0≤t≤1.

证明: 由于(ln(t),wn(t))≥(ur(t),vr(t))在[0,1]上成立与(ln(t),wn(t))≤(Ur(t),Vr(t))在[0,1]上成立本质上一致, 所以本文只证明后者即可.

(14)

对式(14)两边关于t从t0到t∈(t0,t2)积分, 得

即

则有w(t0)≤w(t2)=0, 矛盾.

类似地, 有wn(t)≤Vr(t), 所以∀t∈[0,1], (ln(t),wn(t))≤(Ur(t),Vr(t)).

证明: 令[a,b]⊂(0,1)是一紧区间, 可得

(15)

其中Cn是方程

的解. 根据积分第一中值定理, 存在ξn∈[a,b], 使得

即

又由引理3知,ur(t)≤ln(t)≤Ur(t), 从而存在M=M(r,a,b)>0, 使得

(16)

(17)

成立. 由式(15)～(17), 有

类似地, 有

根据引理4, 可以证明:

(18)

其中τ=φ(l′(1/2))是方程

(19)

的解. 综上可得l(t)=(Tl)(t), 类似可证w(t)=(Tw)(t). 因此, (l,w)=(T(l,w))(t)是式(9)的解.

由于D是C[0,1]×C[0,1]中的任意有界集, 于是有:

引理6T:C[0,1]×C[0,1]→C[0,1]×C[0,1]全连续.

对问题(1)利用Schauder不动点定理和Leray-Schauder非线性抉择定理可得更一般的存在性原则.

定理1假设(H1)和(H2)成立. 设存在常数M>A+B(不依赖于λ), 且

(20)

其中(x,y)∈C[0,1]×C[0,1]∩C1(0,1)×C1(0,1)是边值问题

(21)λ

的解,λ∈(0,1). 则问题(1)存在一个解(x,y)且满足‖(x,y)‖≤M.

证明: 式(21)λ等价于不动点问题

(x,y)=λT(x,y), (x,y)∈C[0,1]×C[0,1],

(22)λ

定理2假设(H1)和(H2)成立. 设存在常数M>A+B(不依赖于λ), 且式(20)成立, 其中(x,y)∈C[0,1]×C[0,1]∩C1(0,1)×C1(0,1)是边值问题

(23)λ

的解,λ∈(0,1). 则问题(1)存在一个解(x,y)且满足‖(x,y)‖≤M.

证明: 式(23)λ等价于不动点问题

(x,y)=(1-λ)(Q,Q)+λT(x,y),Q=A(1-t)+Bt.

(24)λ

证明: 问题(1)等价于不动点问题(x,y)=T(x,y). 因为T:C[0,1]×C[0,1]→C[0,1]×C[0,1]全连续, 则利用Schauder不动点定理可证得结论.

[1] Agarwal R P, O’Regan D. Existence Theory for Single and Multiple Solutions to Singular Positone Boundary Value Problems [J]. J Differential Equations, 2001, 175(2): 393-414.

[2] JIANG Da-qing, GAO Wen-jie. Upper and Lower Solution Method and a Singular Boundary Value Problem for the One-Dimensionp-Laplacian [J]. J Math Anal Appl, 2000, 252(2): 631-648.

[3] JIANG Da-qing, LIU Hui-zhao. On the Existence of Nonnegative Radial Solutions forp-Laplacian Elliptic Systems [J]. Ann Polon Math, 1999, 71(1): 19-29.

[4] JIANG Da-qing. Upper and Lower Solutions Method and a Superlinear Singular Boundary Value Problem for the One-Dimensionalp-Laplacian [J]. Computers and Mathematics with Applications, 2001, 42(6/7): 927-940.

[6] WANG Jun-yu, GAO Wen-jie. A Singular Boundary Value Problem for the One-Dimensionalp-Laplacian [J]. J Math Anal Appl, 1996, 201(3): 851-866.

[7] KONG Ling-bin, WANG Jun-yu. Multiple Positive Solutions for the One-Dimensionalp-Laplacian [J]. Nonlinear Anal: Theory, Methods and Applications, 2000, 42(8): 1327-1333.

[8] ZHANG Mei-rong. Nonuniform Nonresonance at the First Eigenvalue of thep-Laplacian [J]. Nonlinear Anal: Theory, Methods and Applications, 1997, 29(1): 41-51.

[9] O’Regan D. Existence Theorey for Nonlinear Ordinary Differential Equations [M]. Dordrecht: Kuwer Academic, 1997.

[10] HU Wei-min, JIANG Da-qing, LUO Ge-xin. Theory for Single and Multiple Solution to Singular Discrete Boundary Value Problems for Second-Order Differential Systems [J]. Dynamic Systems and Applications, 2008, 17: 221-234.

[11] QIAN Mei-hua, CONG Fu-zhong, XU Xiao-jie. Existence of Twin Positive Solutions for Singular Second Order Differential Systems [J]. Journal of Jilin University: Science Edition, 2010, 48(5): 755-760. (千美华, 从福仲, 许晓婕. 奇异二阶方程组两个正解的存在性 [J]. 吉林大学学报: 理学版, 2010, 48(5): 755-760.)

[12] O’Rrgan D, Agarwal R P. Existence Theory for Single and Multiple Solutions to Singular Boundary Value Problems for One-Dimensionp-Laplacian [J]. Advances in Mathematical Science and Applications, 2003, 13(1): 179-199.

[13] SHEN Qin-rui, ZHOU Zong-fu. Existence of Perodic Solution for a Class of Third-Orderp-Laplacian Equation with a Deviating Argument [J]. Journal of Jilin University: Science Edition, 2012, 50(1): 27-34. (沈钦锐, 周宗福. 一类具偏差变元的三阶p-Laplacian方程周期解的存在性 [J]. 吉林大学学报: 理学版, 2012, 50(1): 27-34.)

[14] SUN Peng, KONG De-jian, LI Jian-jun, et al. Blow-Up and Global Existence of Positive Solutions for Inhomogenous Evolutionp-Laplacian Equations [J]. Journal of Northeast Normal University: Natural Science Edition, 2012, 44(1): 1-9. (孙鹏, 孔德建, 李建军, 等. 非奇次发展型p-Laplacian 方程正解的爆破性和存在性 [J]. 东北师大学报: 自然科学版, 2012, 44(1): 1-9.)

[15] WEN Xiang-dan, YUAN Cheng-jun, JIANG Da-qing. Solutions to Perodic Boundary Value Problems of a First Order Singular Coupled Systems [J]. Journal of Natural Science of Heilongjiang University, 2011, 28(6): 763-766. (文香丹, 苑成军, 蒋达清. 一阶奇异耦合方程组周期边值问题的解 [J]. 黑龙江大学自然科学学报, 2011, 28(6): 763-766.)