一类最优投资理论的数学模型

任长宇, 袁 芳

(1. 吉林大学 数学学院, 长春 130012; 2. 香港浸会大学 数学系, 香港)

0 引 言

雍炯敏[1]研究了金融数学中的一类最优投资问题, 目标是寻找最优投资组合, 以最优化该投资者的收益, 他把这类问题归结为如下抛物型Monge-Ampère方程：

(1)

注意到方程(1)中自变量y的意义是“该投资者用于投资的初始资本”, 则显然当y<0时该投资者无法进行投资. 同时, 作为“初始资本”, 必然是有限的. 因此, 为了与这种投资问题的实际更接近, 应该代替纯粹的初值问题(1)而考虑区域Q=[0,T)×(0,X)上的初边值问题. 文献[5]对该问题的第一初边值问题进行了一些基础性研究, 在给定的结构条件下, 建立了相关问题古典解的存在唯一性.

本文进一步研究由模型(1)导出的如下抛物型Monge-Ampère方程的混合初边值问题：

(2)

这里:u(x,t)是未知函数;f(x,t)和φ(x,0)分别是Q和[0,X]上的适当光滑函数;A(t),B(t)为[0,T]上的函数;a,b为非负常数. 此外, 还需下列基本假设:

(H3) 问题(2)满足直到二阶为止的衔接条件.

在问题(2)中, 为方便, 用φ(x,0)表示g(x). 由于本文考虑混合初边值问题, 因此条件(H2)与文献[5]中的条件有不同之处.

记

函数v(x,t)∈K称为可容许函数. 显然, 对任意的可容许函数u(x,t)∈K, 问题(2)为抛物型方程. 本文将在K中寻找问题(2)的可容许解. 主要结果如下:

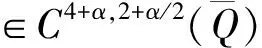
注1文献[5]中保留了问题(1)的条件g′(x)≤0, 本文可以去掉.

注2当r=0时, 问题(2)中的方程恰好是文献[6-7]中所讨论方程的一维情形. 因此本文只考虑r>0的情况.

注3当a=b=0时, 问题(2)恰好与献[5]中所研究的问题相同. 因此本文也可视为文献[5]中所述问题的进一步研究.

为简便, 本文不妨假设函数φ(x,t)已经光滑延拓到整个Q, 并且

-[φt(x,t)-rxφx(x,t)]φxx(x,t)=f(x,t), ∀(x,t)∈[0,X]×{t=0}.

(3)

1 解的存在性

对τ∈[0,1], 考虑如下单参数问题族:

(4)τ

其中:

Aτ(t)=(1-τ)A0(t)+τA(t);Bτ(t)=(1-τ)B0(t)+τB(t);

显然, 当τ=1时, 问题(4)τ即为问题(2).

从而问题(4)0在K中有解.

证明: 令

u0(x,t)=φ(x,0)+(ert-1)(x2-Xx)-kt,

(5)

命题1确保了单参数问题族(4)τ的解集合不空. 如果能事先得到问题族(4)τ的所有可能解的C2+α,1+α/2估计:

(6)

这里:α∈(0,1);C>0为可控常数. 则问题(2)解的存在性可以通过经典的连续性方法得到[6,8-9]. 不难验证, 从“问题数据”的角度看, 问题(4)τ和问题(2)具有相同的性质, 因此只需对问题(2)的所有可能解u=u(x,t)做出与式(6)相同的先验估计即可.

2 先验估计

为了证明解的唯一性及做先验估计, 先证明一个比较原理.

引理1设v(x,t),w(x,t)∈K满足如下不等式:

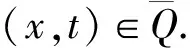
证明: 先证明式(7)-(10)中不等号均为严格不等号的情况.

v-w≤(v-w)x=0,X<0,

-(vt-rxvx)vxx≤-(wt-rxwx)wxx于(x0,t0),

对于式(7)-(10)中不等式的情形, 可取ε>0充分小, 令vε(x,t)=v(x,t)-ε(t+1), 则容易验证

由命题1直接可得:

定理2问题(7)-(10)在K中至多有一个解.

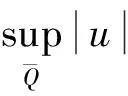
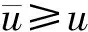
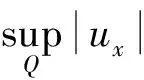
综上, 有:

命题2设u∈K为问题(2)的可容许解, 则存在一个仅依赖于问题数据的常数C1, 使得

下面估计ut, 考虑问题(2)中方程的线性化算子:

关于ut的先验估计, 有:

命题3设u∈K为问题(2)的解, 则存在仅依赖于问题数据的常数C2,c0>0, 使得

(11)

下面分3种情形讨论:

由式(11)和(2)中第三式, 有

由式(11)和(2)中第四式, 有

综上, 结合命题2即可得-ut的上方估计.

下面做-ut的下方估计. 对相同的抛物算子Lu, 考虑如下两个辅助函数:

w1=ek1tut,w2=rxuxek1t.

直接计算得

于是

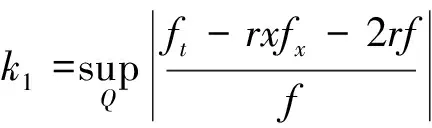
下面分3种情形讨论:

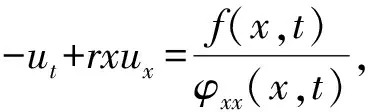
ek1t0(-uxt+rux)≥0;

由式(11)和(2)中第三式, 有

ek1t0(-uxt+rux+rXuxx)≤0;

由式(11)和(2)中第四式, 有

最后, 估计uxx. 由于已经得出了-(ut-rxux)≥c0>0, 因此直接利用方程(2), 可得:

命题4设u∈K为问题(2)的解, 则存在仅依赖于问题数据的常数ν0,C3, 使得

将式(2)中的方程两边对t求导, 得

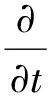
(12)

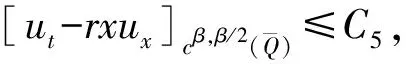
综上, 可得:

定理3设u∈K为问题(2)的解, 则存在可控常数β∈(0,1)和C>0, 使得

利用连续性方法, 综合上述结果即可完成定理1的证明.

[1] 雍炯敏. 数学金融学: 理论与实践 [M]. 北京: 高等教育出版社, 2000.

[2] WANG Guang-lie, LIAN Song-zhe. An Initial Value Problem for Parabolic Monge-Ampère Equation from Investment Theory [J]. J Partial Differential Equations, 2003, 16(4): 381-383.

[3] WANG Guang-lie, LIAN Song-zhe. On the Initial Value Problem for a Parabolic Monge-Ampère Equation [J]. Northeast Math J, 2003, 19(2): 103-106.

[4] LIAN Song-zhe. Existence of Solutions to Initial Value Problem for a Parabolic Monge-Ampère Equation and Application [J]. Nonlinear Anal, 2006, 65(1): 59-78.

[5] REN Chang-yu, CHEN Mo. The First Initial-Boundary Value Problem of Parabolic Monge-Ampère Equation Come from Optimal Investment [J]. Journal of Jilin University: Science Edition, 2009, 47(5): 866-870. (任长宇, 陈默. 一个源于最优投资理论的抛物型Monge-Ampère方程的第一初边值问题 [J]. 吉林大学学报: 理学版, 2009, 47(5): 866-870.)

[6] WANG Guang-lie. The First Boundary Value Problem for Parabolic Monge-Ampère Equation [J]. Northeast Math J, 1987, 3: 463-478.

[7] REN Chang-yu, CHEN Mo, LI Zhi-jun. The Third Initial-Boundary Value Problem of Parabolic Monge-Ampère Equation with a General Form [J]. Journal of Jilin University: Science Edition, 2011, 49(4): 587-593. (任长宇, 陈默, 李志军. 一类一般形式抛物型Monge-Ampère方程的第三初边值问题 [J]. 吉林大学学报: 理学版, 2011, 49(4): 587-593.)

[8] Ivochkina N M, Ladyzhenskaya O A. Parabolic Equations Generated by Symmetric Functions of the Eigenvalues of the Hessian or by the Principal Curvatures of a Surface.Ⅰ.Parabolic Monge-Ampère Equations [J]. Algebrai Analiz, 1994, 6(3): 141-160.

[9] REN Chang-yu, WANG Guang-lie. A Class of Parabolic Monge-Ampère Equation with a More General Form [J]. Journal of Jilin University: Science Edition, 2006, 44(1): 30-38. (任长宇, 王光烈. 某种更一般形式的抛物型Monge-Ampère方程 [J]. 吉林大学学报: 理学版, 2006, 44(1): 30-38.)