基于Monte Carlo方法的战斗部部件质心偏移量仿真分析
2012-12-03葛任伟欧阳勇
葛任伟 欧阳勇 李 佳
中国工程物理研究院,绵阳,621900
0 引言
由于加工、装配、材料特性等不确定性因素的存在,导弹的实际质心位置往往偏离理论期望值而产生质心偏移。对于高速运动中的导弹,当其质心偏移量超差时,容易造成导弹偏离轨道而影响控制精度,甚至造成坠毁[1]。随着导弹技术的进一步发展,远程化、高命中率已成为导弹的发展方向之一,而随着飞行速度的增快,其在飞行过程中受到质心偏移因素的影响也越来越大。
通常,在导弹完成装配后,可以通过测量装置获得质心位置的实测值,如质心偏移超差,可通过质量配平的方式进行调整,使其满足要求。然而,这种方式属于后验方法,虽可以使产品满足要求,在一定程度上却是以牺牲其他性能为代价,如增加配平质量等。若能在早期设计阶段,及时掌握质心偏移的情况,通过理论计算对相关因素进行分析,并采取一定的措施控制质心偏移的范围,不仅可以提高产品的质量,而且还能大大缩减后期进行质量配平的工作流程及时间。本文以某导弹战斗部部件为例,探讨在设计阶段由于给定的尺寸误差引起的导弹质心偏移量大小的计算方法。
1 质心偏移量计算
1.1 质心偏移产生的原因
考虑加工、安装等因素,导弹零部件的设计尺寸通常带有一定的公差;加工时,零部件的实际尺寸误差具有一定的随机性;装配过程中,误差会按尺寸链的方向传递,使质心偏离预期位置,多个组件叠加的效果使导弹产生质心偏移。下面以某导弹战斗部部件为例,分析质心偏移产生的原因。
某战斗部部件由安装板与其上布置的组件M1,M2,…,Mn组成,每个组件均通过螺钉与安装板连接,如图1所示。图中oz方向为弹头飞行方向,ox、oy分别为安装板的舵面线方向,o为坐标原点,位于安装板的圆心。令部件ox方向的质心位置函数为fx(X),部件质心期望位置为安装板中心,即坐标原点,则fx(X)与组件质量、位置参数之间的函数关系为
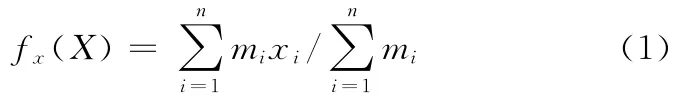
式中,X、fx(X)、mi、xi分别为组件在ox 方向上的位移量、质心位置函数、组件质量和组件质心距坐标原点的距离。
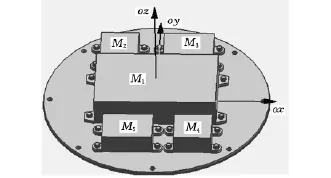
图1 模型示意图
设计期望fx(X)=0,但由于尺寸偏差、质量误差存在的必然性,使得质心偏离预期位置,即fx(X)≠0,组件产生质心偏移,其数值大小为质心偏移量。为了减小质心偏移对导弹飞行性能的影响,一般要求fx(X)小于某一给定值。同时由式(1)可以看出,影响质心偏移的因素为各组件的质量及其距组件理论质心的距离,组件的质量通常不会随装配等因素而改变,因此,影响组件质心偏移量的因素为组件质心的位移。
在实际工程应用中,x、y方向均会出现误差,此时的质心偏移量计算公式为
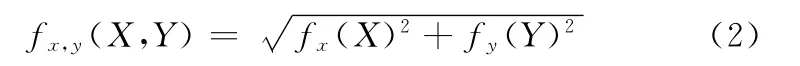
式中,fx,y(X,Y)、fy(Y)分别为组件在xoy 平面的质心位置函数及组件在oy方向的质心位置函数。
1.2 组件装配尺寸链分析
图2所示为装配尺寸链示意图,以其中的第i个组件为例,分析装配尺寸链中尺寸误差对组件质心偏移量的影响,装配完成后的组件质心在ox方向的尺寸链为[2-4]
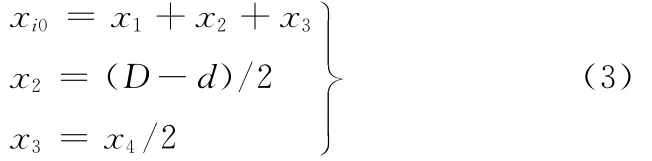
式中,xi0为 尺 寸 链 封 闭 环;x1、x2、x3、x4为 尺 寸 链 组 成环;D为组件安装孔直径;d为螺钉直径。
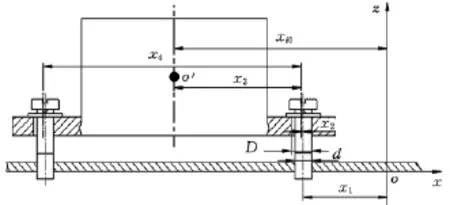
图2 装配尺寸链示意图
x1、x2、x3、x4通常会给定设计误差,xi0也不可避免地存在误差,其大小由式(3)决定。同样,可以分析得出oy方向的尺寸链及其误差。
通常采用极值法与Monte Carlo方法计算质心偏移量。
1.3 基于极值法的质心偏移量计算方法
极值法也叫最差情况法,分析的重点是质心偏移量范围的变化,是组件质心位置的最大变动或最小变动范围的综合结果,仅考虑尺寸误差最坏时的极端情况。极值法计算质心偏移量大小的公式为
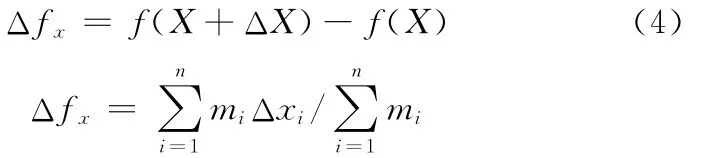
同理
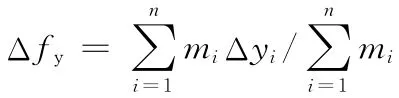
然后通过式(2)计算得到组件质心偏移量。
1.4 基于Monte Carlo方法的质心偏移量计算方法
Monte Carlo方法通过随机模拟和统计试验来求解数学、物理和工程技术问题的近似解,是一种根据各个单独变量的分布形式来求解具有多个变量函数分布的方法[5-6]。该方法从所有变量的分布形式中取样,并把由此得到的各值代入到有关函数中,求得一个函数值,将这一过程重复相当多的次数,便得到若干个函数值,然后估计出这些变量函数值的分布和参数。用Monte Carlo方法模拟进行质心偏差分析包括以下内容:
(1)确定变量概率密度函数。由于尺寸误差、装配位置的随机性,导致组件质心位置具有随机性,其位置误差通常服从一定的概率分布。由式(3)可知,每个组件质心位置是其装配尺寸链组成环的函数,组成环的概率分布形式,决定了组件质心位置的分布情况。
(2)产生随机数、抽样。为了模拟各组成环尺寸,模拟产生大量的服从(0,1)上均匀分布的随机数,根据各组成环尺寸误差的概率分布形式及其相关性,将产生的服从(0,1)上均匀分布的随机数抽样转换为满足分布形式的随机数。为了便于讨论,本文假设组成环参数之间相互独立,且概率密度函数服从正态分布,以获得一组等价于尺寸及公差实际值的随机数。
(3)确定质心偏移函数。安装板上组件的质心位置封闭环之间为相互独立的随机变量,导弹战斗部部件质心位置可看作是这些随机变量的多维随机函数:
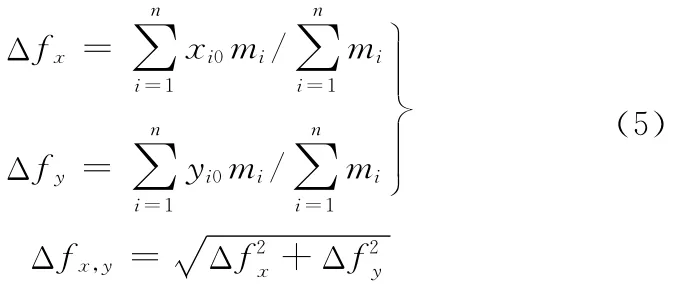
(4)统计模拟结果。通过质心偏移函数就可获得大量的 Δfx、Δfy和 Δfx,y,对其进行统计分析得到均值、方差等统计量[7-8],然后对结果进行评判分析。
2 计算示例
现以图1为例,对采用极值法与Monte Carlo方法获得的质心偏移量进行对比分析,假设设计时要求的导弹战斗部部件质心偏移量不大0.45mm,其给定的组件在ox、oy方向上的尺寸、误差及分布参数相同,如表1所示。
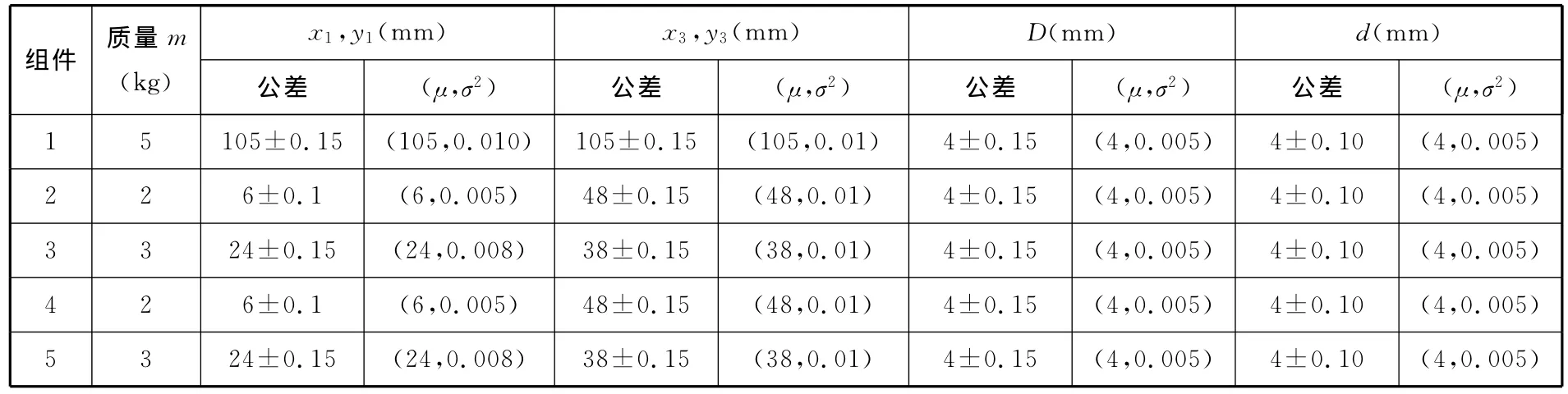
表1 计算参数
将表1中的参数代入式(4),得到组件在ox、oy方向上的质心偏移量范围均为(-0.4116,0.4116)mm。组件在xoy平面的质心偏移量范围为(0,0.58)mm,超出了设定值,需进一步缩小各个尺寸的误差,以满足设计指标,这将增加产品的加工难度及成本。
借助MATLAB软件的计算功能,按照1.4节中的分析内容,根据表1中的数据,产生正态分布的随机数,即各组成环的模拟数据样本,将其代入质心位置函数,得到质心偏移的模拟数据样本。当抽样次数n′为1×104、1×106和4×106时,利用式(5)计算组件在ox、oy方向上的质心位置以及组件的质心偏移量,得到Δfx、Δfy的均值、标准差以及Δfx,y的统计数据。由于组件在ox、oy方向上采用了相同的尺寸、误差及分布参数,故计算所获得的Δfx与Δfy的均值、标准差相同,数据如表2所示。图3a~图3c所示为Δfx、Δfy的数据样本统计图;图3d~ 图3f所示为Δfx,y的数据样本统计图。
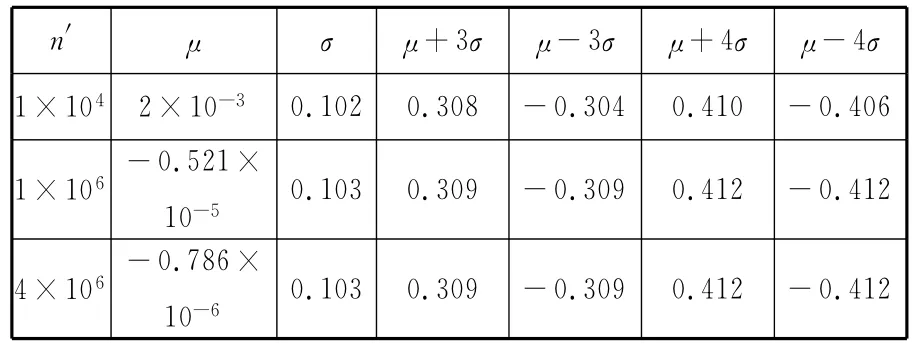
表2 抽样计算结果
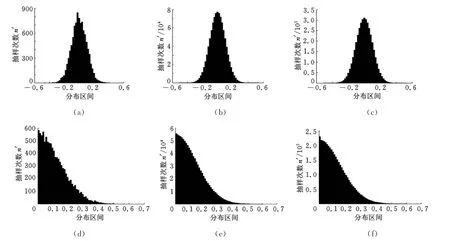
图3 模拟样本数据统计结果
由表2与图3a~图3c可知,部件质心位置在ox、oy 方向上以99.73% 的概率位于(-0.308,0.308)mm 之 间,以 99.9937% 的 概 率 位 于(-0.412,0.412)mm 之间,在ox、oy 方向上的质心偏移量大于0.45mm的几率非常小。由图3d~图3f可知,组件在xoy平面质心偏移量的分布形式与正态分布函数大于零时的情况相近,这是由于尺寸误差基于正态分布假设,质心偏移量在计算时只取正值的结果。进一步计算可以得到Δfx,y小于0.45mm 的概率为99.79%,大于极值法计算结果0.58mm的概率为0.0065%。可见采用极值法计算得到的结果近于小概率事件,而采用Monte Carlo方法更符合实际情况。因此,可先在设计阶段根据给定的尺寸误差预估质心偏移量的大小,再根据计算结果合理地调整设计公差,达到有效降低产品加工难度的目的。
3 结语
本文基于Monte Carlo方法,以某导弹战斗部部件分析了尺寸误差对其质心偏移的影响,对比分析了采用极值法与Monte Carlo方法计算质心偏差的结果。极值法计算的所有尺寸偏差的最大值通常反映的是质心偏移量的范围,近于小概率事件,故难以客观地反映实际的情况。Monte Carlo方法因其是基于大多数机械化零件在公差范围内呈正态概率分布的事实进行计算,所以其计算结果通常更加符合实际的工程情况。本文分析表明,若在设计的初期,根据设计分配的尺寸误差,利用Monte Carlo方法进行计算,则可以有效地掌握产品质心偏移量的大小,为合理分配公差提供指导。
[1]杜明芳,张之江,陆利坤.飞行物体质心的测定[J].计量技术,2002(9):31-32.
[2]屈建喜.圆柱孔定位误差分析及计算[J].金属加工,2008(24):46-47.
[3]李仲辉,鲁世红.考虑形位公差的装配公差分析[J].机械工程与自动化,2010,160(3):105-107.
[4]高庆丰,夏群力,方蜀州,等.安装误差和动不平衡对旋转导弹惯性器件输出的影响及补偿[J].北京理工大学学报,2010,30(7):765-770.
[5]韩雪冰,张景旭,赵金宇,等.水平式光电望远镜目标定位误差的预测[J].光学精密工程,2010,18(7):1595-1604.
[6]郭鹏飞,阎绍泽.含间隙四连杆机构运动误差的Monte Carlo模拟[J].清华大学学报(自然科学版),2007,47(11):1989-1903.
[7]袁贵星,王平.蒙特卡洛模拟及其在公差设计中的应用[J].天津科技大学学报,2008,23(2):60-64.
[8]李自良,黄惠明,王乃卫.基于蒙特卡罗方法的误差传播与误差分配计算[J].装备指挥技术学院学报,2003,14(3):98-101.
