静电微泵的3D流固耦合动态特性分析
2012-12-03董金新林谢昭
董金新 林谢昭 应 济 李 俊
1.温州职业技术学院,温州,325035 2.浙江大学,杭州,310027
0 引言
微流体系统中大都要求有微泵。其中,薄膜往复振动式无阀微泵是以扩散/收缩单元为阀门,通过泵膜的振动驱动流体,其制造简单,可以驱动一些非均相的流体,是众多研究的焦点。根据驱动原理不同,无阀微泵可划分为电磁、静电、压电、形状记忆合金等多种类型。其中,静电无阀微泵具有较低功耗,易于与IC工艺集成兼容等优点,而得到广泛关注。
由于微泵的尺度很小,薄膜往复振动式无阀微泵的绝大部分物理量难以通过实验测量,特别是瞬态量。因此,在微泵的研制阶段,利用数值方法对动态性能进行仿真、预测显得很重要。它不仅可降低费用,而且能更好地了解微泵的工作原理以及可能的潜在缺陷。但因微泵中柔性泵膜、电驱动和流体相互耦合,加之流体在扩散/收缩单元中的不同流动方向表现出的不同压力特性,增加了对整个泵的仿真难度和复杂性。早期的研究采用低阶集总参数模型[1-2]和等效电网络模型[3]等简化方法,忽略了参数的空间分布特性。目前大部分的研究没有考虑泵的流固耦合效应,也无法建立电驱动信号量与流体动力学量(比如流量)之间的关系。或是研究驱动器的动态特性[4-7];或是简化流体场,根据扩散/收缩单元的压力损失系数,将泵膜的运动与泵腔内外压力以及扩散/收缩单元流量联系起来,研究泵膜的动态特性[8-11];或是将驱动器的位移输出,作为流体场的移动壁面问题来研究泵流体的动力学特性[12-14]。实际上,泵膜的动态特性与流体黏滞损失的非线性和不稳定性等是相互影响的。为了理解整个微泵的动态特性,模型必须能有效地描述这些耦合效应[15-16]。本文以静电无阀微泵为对象,建立静电-结构-流体全耦合的3维模型,利用数值方法,仿真并分析各个变量的非线性动态特性。
1 模型的建立
1.1 控制方程、边界条件以及初始条件
图1所示为静电无阀微泵的结构示意图。对于泵送流体,采用任意拉格朗日-欧拉(ALE)描述比较方便。某一时刻,在参考系中^x位置流动的流体质点速度u的时间导数可以表示为
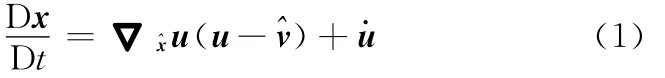
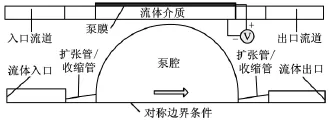
图1 静电无阀微泵的结构示意图
流体域Ωf的不可压缩流动动量守恒定律以及连续方程可以表示为
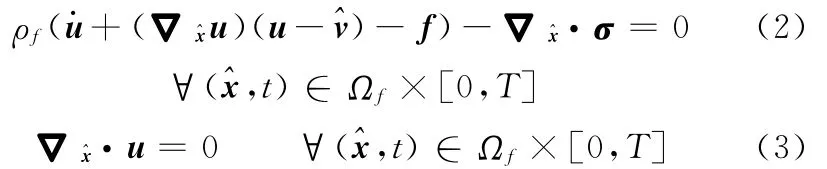
式中,ρf、f、σ分别为流体密度、体积力向量和Cauchy应力张量;[0,T]为所考察的时间间隔。
牛顿流体的本构方程为
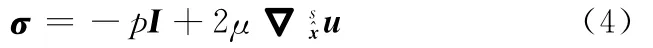
在泵膜流固耦合界面Γf-s处,边界条件如下:
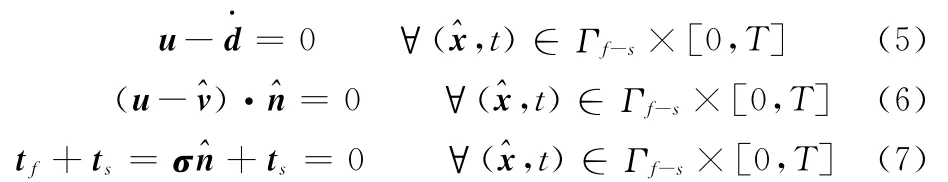
式(5)为流固界面Γf-s处的无滑移条件;在流固界面Γf-s上,参考系的速度^v及其位置^x需要满足连续条件式(6),以保证参考系的边界准确地表达结构的当前构型。沿着界面的应力平衡由式(7)表达。
对于泵膜,可以利用标准的Lagrangian描述建立其运动学方程,即
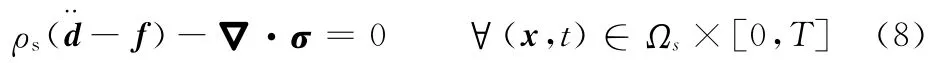
式中,ρs为固体的密度。
泵膜流固耦合边界Γf-s满足:
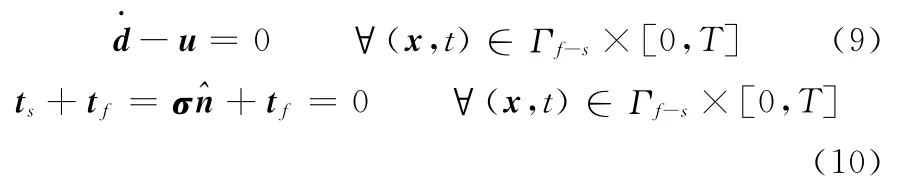
边界条件式(9)、式(10)分别对应于式(5)和式(7)。
如果没有包含自由电荷,则描述静电场的Poisson方程可以表示为
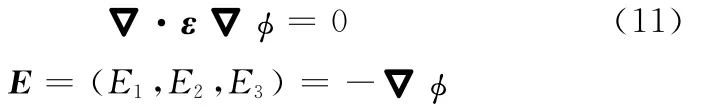
式中,φ为静电势;ε为介电常数张量;E为静电场电场强度。
Maxwell静电应力张量TE由下式计算:
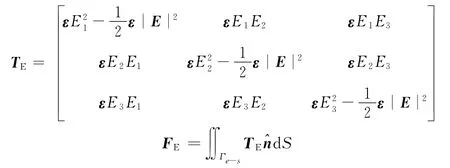
式中,FE为静电载荷。
各个场变量的初始条件都设置为零。为了计算易于收敛,将一个很小的初值输入到模型中。
1.2 模型参数及材料属性
图1所示静电微泵的泵膜厚度为10μm,泵腔深度为100μm,泵膜半径为2000μm;扩散/收缩单元的几何结构相同,长度为1000μm,最小端面宽度尺寸为80μm,扩张角为10°;连接的进出口管道长度皆为2000μm,宽度为200μm。流体介质为去离子水,物性参数如表1所示。
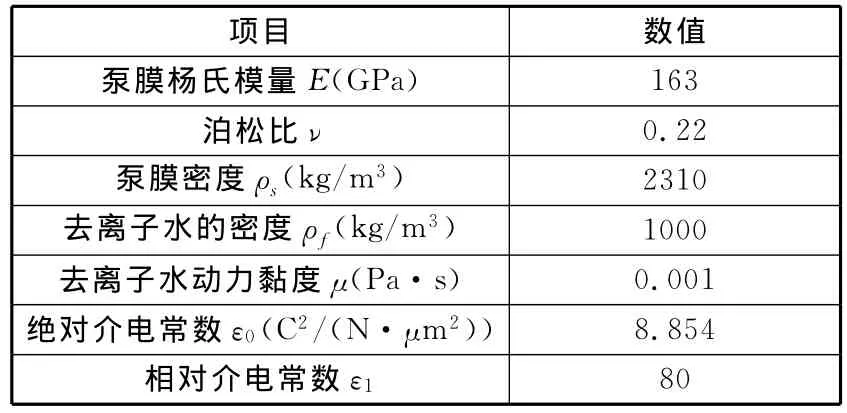
表1 与微泵仿真相关的材料属性参数
假设层流流动,考虑对称性,在CFD-ACE中建立微泵的一半模型。利用结构化网格划分流体,单元数为52 880个,泵膜划分为4974个壳单元。使用基于压力修正的SIMPLE-C 算法对流动以及能量进行顺序积分,获得流场的解。流体域的对流和扩散采用一阶迎风格式,时间积分采用了Crank-Nicolson格式。使用基于有限体积法的计算格式求解静电场,这样可以处理不同介质介电常数问题。利用一阶壳单元来表达泵膜,并进行大变形和接触等几何非线性分析。考虑到静电、结构以及流动耦合求解的需要,利用网格重划分工具,使用预测-校正方法对局部变形进行连续修正,将流动速度和结构速度联系起来,实现流固耦合分析。流体和结构求解器的耦合迭代频率设置为fc=1,使得流体场和结构场信息能及时得到交换和更新。当量纲一残差小于10-4时,认为计算是收敛的。施加的周期性驱动电压V=200(1-cos(20πt))(泵腔底电压为零),在Pentium-3.0GHz的PC机中,完成3.5个周期的求解,共350个子步数,求解时间约为59h。
2 结果及讨论
2.1 泵膜的动力学特性
图2所示为计算得到的泵膜中心点垂直方向上的位移随时间变化曲线,图中最大变形量为28.433μm。考虑流固耦合效应后,在流体阻尼作用下,泵膜无法回复至初始零位置,0.653μm为新的平衡位置。稳态情况下,泵膜位移的变化滞后于输入电压信号的变化,一个周期的滞后时间约为0.01s。

图2 泵膜中心垂直方向上的位移随时间变化曲线
2.2 流场的瞬态特性
实际上,泵流体动态特性更为设计者所关注,为了更好地诠释泵膜振动与流体特性之间的耦合关系,用图3所示的泵膜流固耦合界面上中心点处的垂直方向位移与泵腔内流体压力来显示其对应关系,从图中可以明显地看出,流体压力的变化与泵膜的位移存在着密切关系。在静电力的作用下,泵膜下拉变形的速度大于回弹的速度,所以在流体压出泵腔的过程中其压力变化较大,最高压力为945.1Pa;而在流体吸入泵腔过程中,其压力变化相对较小,最大负压为-558.0Pa;整个泵送过程中,流体压力呈现非对称性变化。图3还表明,泵初始工作点从零点开始,经过第一个周期的瞬态过程后,第二个周期的轨迹与第三个周期的轨迹已经重合,表明泵已经进入稳定工作状态。流体压力的波动周期同样滞后于驱动电压的变化(约0.01s)。
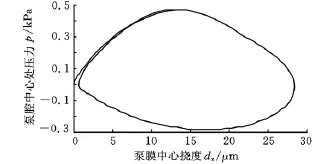
图3 泵膜中心点处垂直方向上位移与流体压力的关系
图4所示为进出口单元处的瞬态体积流量变化曲线,从图中可以看出,在泵膜下拉(往固定电极)运动阶段(泵送阶段),出口单元的瞬态流量大于进口单元的瞬态流量;而在泵膜回弹阶段(泵吸入阶段),进口单元的流量则大于出口单元的流量。最大的瞬态流量差发生在泵腔内压力达到极大值时刻,而在泵腔内压力与进出口压力相差不大的时间段,进出口单元的流量相差不大。表明要使扩散/收缩单元发挥“整流”作用,其两端的压力差必须达到一定值,并且压力差要尽可能地大。对稳态情况下的泵净流量进行积分计算,得到的净输出流量为10.764nL/s。
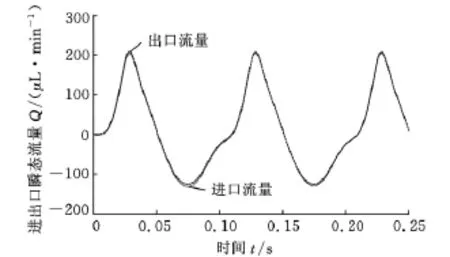
图4 进出口瞬态流量随时间的变化
图5所示为微泵横截面方向上流体压力的分布情况,由图可知泵腔内的压力几乎分布一致,说明在平面布置的无阀微泵中,采用Reynolds方程来描述泵腔内流体的瞬态动力学特性具有一定的可行性。另外,微泵所连接的进出口管道对微泵的工作性能也有影响。
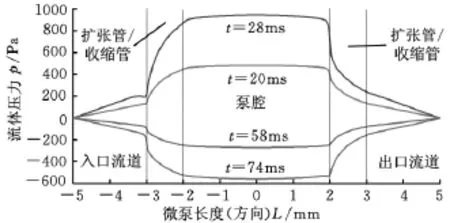
图5 不同时刻下的微泵横截面方向上的压力分布情况
考虑了流固耦合特性后,模型不仅能够仿真泵流场的动态特性,还能够仿真泵膜的应力特性变化。图6所示为t=28ms时刻的泵腔内流体压力分布与泵膜应力分布情况,以及这一时刻的扩散/收缩单元内流体的速度场分布。此时,泵腔内流体压力达到最大值945.3Pa,泵膜中心挠度为13.20μm;泵 膜 边 缘 处 VonMises 应 力 为28.39MPa。微泵腔内的流速较小,扩张管/收缩管颈部的平均流速达到最大,计算得到的平均流速为0.0867m/s,雷诺数为7.71,远小于宏观条件下通常认定的临界雷诺数(2000左右),这也证实了前面假设层流流动模式的正确性。另外,图6b和图6c表明,收缩/扩散管内未出现流体与固体壁面分离流动现象。

图6 t=28ms时刻的泵膜应力和微泵的流体场瞬态结果
3 结论
(1)扩散/收缩单元的最大流量差都发生在泵腔内压力与进出口压力相差最大的时刻,表明要使得扩散单元发挥“整流”作用,其单元两端的压力差必须达到一定值。
(2)在仿真的每个时刻,泵腔内流体压力分布几乎一致,表明用Reynolds方程来描述泵腔内流体动力学特性具有可行性。
(3)仿真得到的最大雷诺数远小于通常认定的临界雷诺数,表明微泵流体具有层流特性。
(4)泵腔内流体动态特性与泵膜的运动存在着密切关系,如果忽略了流固耦合效应,简单地将微泵的驱动器与腔内的流场分离处理,必然歪曲了泵流体场的动态特性。泵膜变形、流体压力和进出口流速等响应与输入电压信号之间存在着滞后现象。对微泵的3D全耦合仿真,能够获得驱动电信号与流体流量、泵送压力等输出变量之间的直接关系,有利于从整体意义上实现微泵的优化设计。
[1]Morris C J,Forster F K.Low-order Modeling of Resonance for Fixed-valve Micropumps Based on First Principles[J].Journal Microelectromech.Syst.,2003,12:325-334.
[2]Olsson A,Stemme G,Stemme E.A Numerical Design Study of the Valveless Diffuser Pump Using a Lumped-mass Model[J].Journal Micromech.Microeng.,1999,9:34-44.
[3]Bourouina T,Grandchamp J P.Modeling Micropumps with Electrical Equivalent Networks[J].Journal Micromech.Microeng.,1996,6:398-404.
[4]Lin X Z,Ying J,Chen Zichen.Research on Terminal Behavior of Electrostatically Actuated Micropump Membrane Based on Modal Analysis[C]//Wei Y L,Chong K T,Takahashi T,et al.ICMIT 2005:Mechatronics,MEMS and Smart Materials,SPIE.Bellingham,2005,6040:P60400U.
[5]Faris W F,Abdel-Rahman E M,Nayfeh A H.Mechanical Behavior of an Electrostatically Actuated Micropump[C]//Agnes G,Chamis C,Noor A,et al.43rd AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Denver,2002:AIAA2002-1303.
[6]Morris C J,Forster F K .Optimization of a Circular Piezoelectric Bimorph for a Micropump Driver[J].Journal Micromech.Microeng.,2000,10:65-459.
[7]王立文,高殿荣,杨林杰,等.压电驱动微泵泵膜振动有限元分析[J].机械工程学报,2006,42(4):230-235.
[8]Ullman A,Fono I.The Piezoelectric Valve-less Pump—improved Dynamic Model[J].Journal Microelectromech.Syst.,2002,11:655-664.
[9]Pan L S,Ng T Y,Wu X H,et al.Analysis of Valveless Micropumps with Inertial Effects[J].Journal Micromech.Microeng.,2003,13:390-399.
[10]MacHauf A,Nemirovsky Y,Dinnar U.A Membrane Micropump Electrostatically Actuated Across the Working Fluid[J].Journal Micromech.Microeng.,2005,15(12):2309.
[11]白兰,冯志庆,吴一辉.无阀微泵动态特性的固液耦合分析[J].机械工程学报,2008,44(7):69-74.
[12]谢海波,傅新,杨华勇.微型无阀泵流动特征仿真与试验研究[J].机械工程学报,2002,38(7):54-57.
[13]杨恺祥.压电无阀式微泵浦制造与测量分析[D].台湾云林县:台湾云林科技大学,2004.
[14]Tsui Y Y,Lu S L.Evaluation of the Performance of a Valveless Micropump by CFD and Lumpedsystem Analyses[J].Sensors and Actuators A:Physical,2008,148(1):138.
[15]Yao Q,Xu D,Pan L S,et al.CFD Simulation of Flows in Valveless Micropumps[J].Eng.Appl.Comput.Fluid Mech.,2007,1(3):181-188.
[16]林谢昭,应济,陈子辰.静电无阀微泵两种仿真模型的比较研究[J].哈尔滨工业大学学报,2010,42(12):1943-1947.
