用计量型AFM对一维纳米基准栅的标定及不确定度估计

黄强先 袁 丹 尤焕杰

合肥工业大学，合肥，230009

0 引言

随着微加工技术、MEMS技术和纳米技术的发展及应用，利用这些技术加工或制备的微器件、MEMS器件及纳米材料等几何尺寸越来越小，相应地对测量精度要求越来越高，甚至要求达到纳米量级及亚纳米量级。目前，已具有纳米量级甚或亚纳米量级分辨率的仪器，如原子力显微镜（AFM）、扫描隧道显微镜（STM）和扫描电子显微镜（SEM）等各种纳米量级测量仪器。上述测量仪器被广泛应用于各种器件需求的测量领域。尽管上述仪器具有极高的空间分辨率，甚或能够分辨出表面原子的位置，但由于上述仪器的测量范围小、测量分辨率高和测量不确定度要求极高，导致上述仪器的精确标定成为目前的世界难题［1－3］。为了方便、可靠地标定上述测量仪器，国际计量局（BIPM）在1998年把纳米尺度线间隔、台阶高度、线宽等5个参数的计量确定为纳米尺度基本特征国际关键比对项目之一［4］，并提出了相应的5种基准样板，以便测量者基于基准样板特征参数确定仪器的测量不确定度。

一维纳米基准栅样板是5个纳米标准样板之一［4］，其平均栅距是该基准样板的特征参数，目前的制作精度达到纳米量级［3，5］。对于该基准栅栅距的标定，既要具有亚纳米量级的测量不确定，又必须使其测量结果溯源到长度基准，目前一般采用计量型原子力显微镜、光学衍射仪等仪器进行标定［1，4，6］。不管采用何种方法和仪器［7］，由于测量仪器复杂、测量环境要求高、测量对象自身加工精度高，以及平均栅距不能直接与长度基准比较，给测量工作带来诸多不便。为了获得可靠的测量结果，需要对测量过程中的各种测量不确定因素进行充分和可靠的分析，从而获得精确的测量结果的测量不确定度。针对轻敲模式计量型AFM的结构特点［8］，本文介绍公称栅距为240nm的一维基准栅的标定，并对其结果进行不确定度分析和估计。

1 一维基准栅与计量型原子力显微镜

1.1 一维基准栅

国际计量局（BIPM）的纳米计量工作组（WGDM7DG）在1998年决定把线宽（Nano 1）、台阶高度（Nano 2）、线刻度尺（Nano 3）、一维栅（Nano 4）和二维栅（Nano 5）作为纳米尺度比对的5种基准样板。本文所采用的一维基准栅是由Hitachi Ltd开发的 HJ－1000标准样板［9］，主要用于纳米测量仪器的标定。该样板是通过激光干涉全析法和各向异性化学刻蚀技术制备的硅样板，样板的实物图及公称尺寸如图1所示。该标准栅的特征参数是平均栅距，公称值为240nm，其制造精度为1nm（3σ）。样板的有效面积约为4mm×4mm。为了便于使用，硅样板被固定于铝金属基板上。

1.2 计量型原子力显微镜

图2所示为AFM系统构成框图，图中，LD为激光二极管，QPD为四象限光电二极管，TSM为三维反射镜载物台。AFM系统由机械系统、悬臂信号处理系统、控制系统、测量系统和控制、数据处理及显示系统等五部分组成［8］。该测量系统与带有闭环控制系统的AFM结构基本相同。所不同的是，该计量型AFM的载物台是由石英材料制作的，且其上方的开口为方槽，如图3所示。该载物台置于三维工作台的上方。载物台的下表面和两相邻侧面正交，并镀有反射膜，因此被称为三维反射镜（TSM）。三反射镜正交性很好，其垂直度误差在1″以内。载物台在x、y、z三维的运动分别用高精度的稳频氦氖激光迈克尔逊干涉仪测量，3个正交反射面分别作为3套干涉测量仪的测量反射镜（图3），因此，载物台在x、y、z方向上的位移测量结果可以长度标准溯源。载物台在x、y方向的位置通过激光干涉仪的位移信号反馈控制，从而完全克服了工作台中压电驱动器非线性、迟滞等的影响。三激光干涉仪的测量线分别与试样的x、y、z运动方向一致，且三测量线正交于AFM探针的针尖处，因此基本消除了阿贝误差。

在每一路激光干涉仪中，测量光路经过4倍光学放大，光信号经过光电转换后又通过软件进行了2048相位细分，即干涉仪的每一个干涉条纹的周期变化与八分之一激光波长的TSM移动量相对应，每一个细分脉冲的变化与工作台的λ／16 384位移量相对应，因此，经信号处理系统处理后的干涉测量系统的分辨率可达到0.04nm。经实验观测，该激光测量系统的非线性误差约为0.12nm，是影响精度的主要误差源之一。

该计量型AFM的x、y、z测量范围分别为17.5μm、17.5μm、2.5μm。该系统原来仅能工作于接触模式，且测量效果不理想，改进后的系统可工作于测量时一般采用的轻敲模式［8］。

2 测量过程与数据预处理

2.1 测量方法与测量过程

一维栅的栅线在4mm×4mm上分布，分布面积较大，实验发现，各处的栅距存在微小的差异。而AFM的扫描区域很小，一般仅为数微米至十微米。为了减小样板均匀性的影响，测量时在样板表面均匀选择9处进行测量，如图4所示。

为了减小阿贝误差，在载物台上安放样板时，应使被测量区域处于三激光干涉仪的测量延长线的交点处。该计量型AFM在扫描一维栅时，采用图5所示的扫描方式，即硅悬臂与一维栅的栅线方向一致。因此，样板还应按照图5所示的方向安放，并尽可能地使栅线方向与y方向平行。图6所示为获得的一个区域的三维图。

测量时，AFM的环境温度、湿度、大气压以及工件的温度等环境参数被实时记录，以用于对计算数据的补偿和不确定度分量的估计。

2.2 数据处理

测量时，每一区域的扫描范围是5μm×5μm，共进行30行扫描、每行获取11 000个点。尽管测量时工作台的x、y位移利用激光干涉仪信号进行闭环反馈控制，但并不能完全消除压电陶瓷的迟滞、蠕变等非线性影响［8］，这种影响在每一扫描区域的开始数行和每行的起始端较大。为了减小对测量结果的影响，在进行数据处理时，每一扫描区域的前10行和每行的前后500个点不参与栅距的计算。

AFM探针在扫描样板时，由于样板的安放误差，探针的扫描方向不可能完全与栅距的方向一致，存在垂直倾角θ和水平偏转角α安装误差（图6）。为了减小这两项角度误差的影响，必须对原始数据进行处理。

图7a所示为样板垂直倾角误差的校正方法。首先，按照线轮廓的顶点确定线轮廓的中心线倾角，该角度被认为就是样板在垂直方向上的安放误差。然后，根据所确定的垂直倾角θ对原始数据进行校正，得到图7a中的中间线轮廓，再根据校正后的线轮廓，按照重心法确定各个栅峰的重心点横坐标［10］。

当每条扫描线上的每个栅峰重心被确定后，即可拟合出图7b所示的栅线方向，该方向与y向的夹角，就是样板在水平面内安放时的偏转误差α，该角度误差将带给栅距计算误差。为了缩小该误差，需要将图7b中左图的重心线校正到中间图的位置，再根据校正后的各重心点确定出各个栅距pi（图7b）。在计算时，上述过程的残余误差将构成两项测量不确定度分量。

通过上述数据处理后的平均栅距为

式中，n为扫描区域内栅距的个数。

表1所示为按照上述测量和数据处理方法，获得的9个区域的算术平均值及相应的单次测量不确定度。

表1 9个不同测量区域的平均栅距、单栅距标准差和平均栅距标准差

根据表1中的数据，9个区域内所有栅距的平均值为240.078nm。

3 不确定度因素分析及估计

利用上述系统按照上述测量过程和数据处理方法，对一维基准栅栅距进行测量、计算，测量结果主要受下面各项因素的影响并导致相应的不确定度分量：

（1）激光频率变化引起的测量不确定度分量u1。稳频氦氖激光器为Spectra－Physics，Model 117A，其Allan方差频率是124kHz，当该数值变化不大于5%时，导致的栅距测量不确定度分量u1为12.1pm，自由度为200.0。按照B类评定方法确定。

（2）温度变化引起的激光死程变化导致的测量不确定度分量u2，该部分是由激光底座温度变化导致底座在激光死程部分热膨胀变化引起的。经测定，温度变化不超过3.2K时，底座可采用因瓦合金制作。经估计，该部分引起的标准不确定分量为1.17fm，自由度为12.5。按照B类评定方法确定。

（3）阿贝误差引起的测量不确定度分量u3。设计时，要求激光干涉仪的测量光路与探针的扫描方向在同一条直线上。但在安装和使用时，由于探针长度不同及其安装误差，会导致两者之间存在最大不超过0.5mm的偏差。经测量，工作台的随机运动误差为0.283×10－2″，近似符合均匀分布。按照B类评定方法估计，该部分引起的标准不确定分量为40.9pm，自由度为200.0。

（4）光路准直误差引起的测量不确定度分量u4。在AFM结构中，激光干涉仪的测量光路应该与干涉仪测量镜反射面完全垂直，但在安装时存在最大｜±0.085°｜的准直误差，该误差将导致工作台位移测量时的余弦误差。该部分引起的测量结果标准不确定分量为16.9fm，自由度为200.0。

（5）光路变化引起的测量不确定度分量u5。在测量时，由于工作台运动误差的存在，除了引起阿贝误差外，还会导致干涉仪反射镜的角位移。而干涉仪反射镜的角位移会使反射光路的变化不稳定，从而导致长度测量误差，该误差为二次误差。按照B类评定方法估计，该部分引起的测量结果标准不确定分量为2.06pm，自由度为200.0。

（6）干涉仪非线性误差u6。干涉仪经过8倍光学细分后，还经过2048次相位细分，由于光路、电路等的不理想，由干涉仪输出的正交电信号并不能构成理想的Lissajow图形，从而造成周期性的非线性误差，如图8所示。按照B类评定方法估计，该误差引起的测量结果标准不确定分量为0.115nm，自由度为200.0。

（7）激光干涉仪分辨率引起的测量不确定度分量u7。根据技术资料，激光干涉仪经过8倍光学细分和2048次电子细分后，按照B类评定方法估计，其导致的栅距测量不确定度分量u7为38.6pm，自由度为200.0。

（8）环境温度、湿度和气压变化引起的测量不确定度分量u8、u9、u10。测量光路周围大气参数的变化将导致光路上大气折射率的变化，从而导致激光频率和波长的变化，引起测量误差。通过实时监测，当环境的温度、相对湿度和大气压的变化不超过1.20K、3.50%和1.50kPa时，由 Edlen公式估计的环境温度、湿度和气压变化引起的测量不 确 定 度 分 量 分 别 为 0.157pm、5.18fm 和0.154pm，按照测试仪器说明，自由度取为12.5。

（9）样板热膨胀引起的测量不确定度分量u11。样板安装在工作台上，由于压电陶瓷管的发热、硅探针振幅检查光路热源等因素的影响，导致了被测尺寸的变化。经实际测量，样板偏离标准室温20℃的最大温差不超过3.2℃，硅样板材料的热膨胀系数为2.6×10－6K－1，温度变化符合均匀分布要求。根据测试仪器说明，按照B类评定方法估计，由样板热变形导致的测量不确定度分量为1.15pm，自由度为12.5。

（10）样板安装误差引起的测量不确定度分量u12、u13。在图7中，虽然通过数据处理可以校正样板2个放置角度带来的主要影响，但由于20行扫描数据的不一致，导致其修正结果分散。通过测量数据分析，按A类评定得到这两项误差带来的不确定度分量分别为1.02pm和1.36pm，自由度为19.0。

（11）重复性引起的测量不确定度分量u14。通过对样板同一测量区域的7次重复测量，得到的单次测量标准差为11.2pm，该标准差可视为重复性引起的测量不确定度分量（按A类评定），自由度取为6.0。

（12）样板各处均匀性引起的测量不确定度分量u15。由于制备工艺原因，样板表面各处的栅距值不一致。为避免不均匀性的影响，一般采用样板内多处均匀取点测量，本文采用了9处取点测量（图4）。将各处不同点的平均值差值标准差作为样板均匀性误差引起的测量不确定度分量，本次测量结果为83.6pm（按A类评定），自由度取为8.0。

（13）区域平均栅距误差引起的测量不确定度分量u16为0.102nm。在本次测量中，测量范围约为5μm×5μm，用其中获得的20行进行平均栅距计算，每行约有21个栅距，共约有420个栅距参与本区域内的平均栅距计算。分析表明，本区域内的栅距分布直方图与图9所示类似。图9是一个测量区域栅距的分布情况，共有420个栅距，其平均栅距为240.13nm，单个栅距的标准差为2.096nm，平均栅距的标准差为0.102nm。该标准差是区域平均栅距的测量不确定度分量（按A类评定），自由度取为419.0。

表2所示为各个因素对测量结果的影响，以及各因素所导致的不确定度分量、评定类型和自由度。在上述各项影响因素中，一般来说，相关性很低或者不相关，且各因素都对平均栅距有直接影响，因此，可按照下述方法确定合成标准不确定度和自由度：

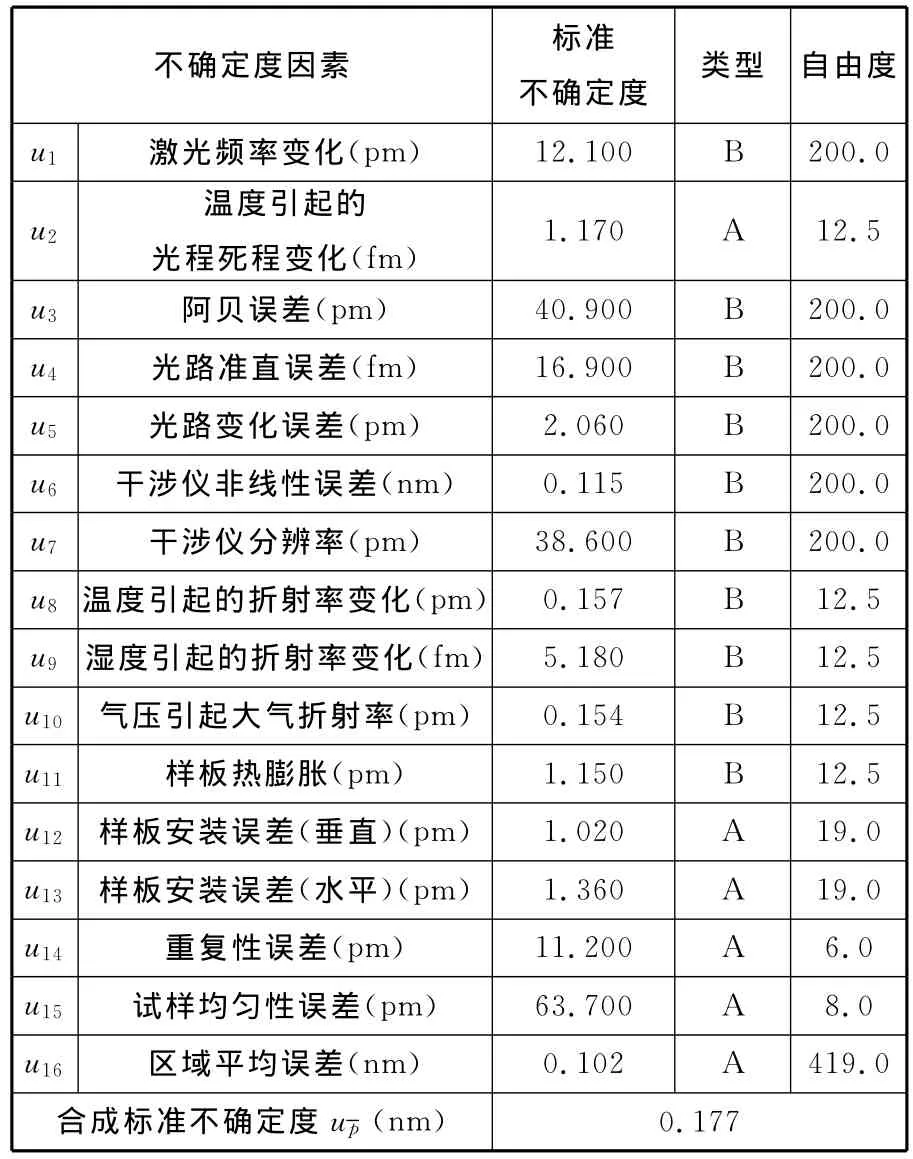
表2 测量结果不确定度分量表

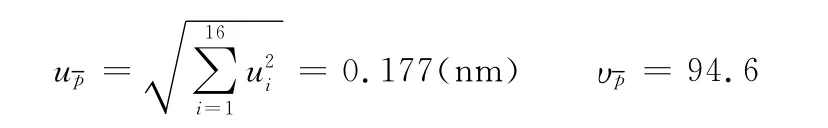
若置信概率取为95%，则平均栅距的扩展不确定度约为0.347nm，其测量结果为（240.078±0.347）nm。

根据上述分析和计算结果，计量型AFM对一维标准栅的标定达到了亚纳米量级精度。同时通过分析发现，在影响测量结果的各个不确定度分量中，除了试样均匀性误差、区域平均误差等一维样板自身具有的误差外，仪器结构的阿贝误差、自身的非线性误差、稳频误差和分辨率、测量过程中的安装误差和环境变化等，都是不可忽略的影响测量不确定度的因素。另外，在进行纳米量级测量时，一些常规测量中可以忽略的误差，如光路变化误差、准直误差等二次误差，也需要充分考虑。

4 结束语

在对轻敲模式计量型原子力显微镜及一维基准栅结构和特性充分了解的基础上，用计量型AFM对一维基准栅的特征参数平均栅距进行了测量。通过对AFM结构和特性参数、一维基准栅特性和参数、测量过程参数、数据处理方法的全面分析，给出了基准栅的平均栅距及测量不确定度分析和估计，扩展不确定度达到0.347nm（扩展因子k＝1.96）。本文测量和分析表明，测量不确定度的确定，不仅需要充分了解测量仪器的结构和参数，而且需要充分了解测量过程中各种参数对测量不确定度的影响；而对于纳米量级测量，常规测量过程中一些可以忽略的二次误差也需要考虑。

［1］Misumi I，Gonda S，Sato O，et al.Nanometric Lateral Scales as CRM Candidates for AFM，SEM and Optical Diffractometer［J］.J.Phy.：Conference Series，2005，13：206－215.

［2］Ritter M，Dziomba T，Kranzmann A，et al.A Landmark－based 3DCalibration Strategy for SPM［J］.Meas.Sci.Technol.，2007，18：404－414.

［3］Nakayama Y，Yamamoto J，Kawada H.Sub－50－nm Pitch Size Grating Reference for CD－SEM Magnification Calibration［C］／／Proceedings of Me－trology，Inspection，and Process Control for Microlithography XXIII.San Jose，USA，2009：727224.

［4］Meli F.WGDM－7：Preliminary Comparison on Nanometrology According to the Rules of CCL Key Comparisons，Nano4：1DGratings，Final Report［R］.Wabern：Swiss Federal Office of Metrology（OFMET），2000.

［5］Nakayama Y，Kawada H，Yoneda S，et al.Novel CD－SEM Calibration Reference Consisting of 100－nm Pitch Grating and Positional Identification Mark［C］／／Proceedings of Metrology，Inspection，and Process Control for Microlithography XXV.San Jose，USA，2011：797119.

［6］Ito Y，Omote K，Okazaki Y，et al.Calibration of 25－nm Pitch Grating Reference by High－resolution Grazing Incidence x－ray Diffraction［C］／／Proceedings of Metrology，Inspection，and Process Control for Microlithography XXIV.San Jose，USA，2010：763810.

［7］Decker J E，Eves B J，Pekelsk J R，et al.Evaluation of Uncertainty in Grating Pitch Measurement by Optical Diffraction Using Monte Carlo Methods［J］.Meas.Sci.Technol.，2001，22（2）：027002

［8］Huang Qiangxian，Gonda S，Misumi I，et al.Nonlinear and Hysteretic Influence of Piezoelectric Actuators in AFMs on Lateral Dimension Measurement［J］.Sens.Actuat.A，2006，125：590－596.

［9］Nakayama Y，Toyoda K.New Submicron Dimension Reference for Electron－beam Metrology System［C］／／Proceedings of Metrology，Inspection，and Process Control for Microlithography III.San Jose，USA，2010：219674.

［10］Huang Qiangxian，Gonda S，Misumi I，et al.Research on Pitch Analysis Methods for Calibration of One－dimensional Grating Standard Based on Nanometrological AFM［C］／／Proceedings of SPIE 6280.Third International Symposium on Precision Mechanical Measurements.Urumiqi，China The International Society for Optical Engineering：2006：628007.