基于静止和运动两种状态的自动导引车视觉标定
2012-12-03楼佩煌王龙军
喻 俊 楼佩煌 武 星 王龙军
南京航空航天大学,南京,210016
0 引言
自动 引 导 车 (automated guided vehicle,AGV)是一种轮式移动机器人,广泛用于工厂自动化生产线、仓储物流、机场和港口中的物料传送[1]。视觉导引方式是通过安装在AGV上的摄像机采集铺设导引路径图像,通过计算机视觉测量算法实时测量AGV相对导引路径的距离偏差和角度偏差。摄像机标定(camera calibration,CC)是计算机视觉测量的一个关键问题,精确的视觉标定能够消除视觉测量的系统误差[2]。
摄像机标定方法主要有传统标定法、主动视觉标定法和自标定法。传统的摄像机标定是将精密制作的立体或平面标靶放置在场景中,利用几何成像原理建立场景中世界坐标点与图像中观测点之间的关系模型,采用线性、非线性法计算摄像机的内外部参数和畸变参数,具有标定精度高的特点[2]。基于主动视觉的标定方法需要控制摄像机做特定运动,如相互正交的平动[3]和绕光轴的旋转运动[4]等,利用参考点的图像坐标变化实现摄像机的内部参数标定。该方法对摄像机运动精度要求苛刻,主要用于工业机器人手眼标定,不适用于摄像机运动自由度受限的场合。
在镜头和摄像机位置均不变的被动视觉导引AGV中,摄像机内外部参数和畸变参数均不变[2]。传统标定法虽然可以获得摄像机的外部参数,但是其计算的外部参数只是标靶坐标系与摄像机坐标系之间的关系。在AGV视觉导航应用中,还需要获得摄像机与AGV坐标系之间的关系,而不借助其他精密测量设备则很难将标靶相对机器人坐标系精确地放置。根据现场标定的要求,本文提出一种基于静止和运动两种状态的AGV视觉标定方法。首先采用静止状态下的平面模型标定法计算内部参数、畸变参数和AGV相对模板的外部参数,建立对三种图像失真进行图像校正的联合模型,再在运动状态下标定出AGV坐标系相对失真校正后图像坐标系的参数。
1 视觉系统模型
摄像机前倾安装方式的AGV[5]视觉系统因其视场较大,精度较低,其标定通常采用基于消失点(vanishing point,VP)的方法[6],这种线性方法只能标定出摄像机安装的俯角和高度,忽略了其他自由度上与理想姿态的误差。本文研究的双向型AGV结构如图1所示。AGV的驱动系统由左右两个独立驱动的驱动轮和前后两个起支撑作用的万向轮组成。这种机构可以通过调节两个驱动轮的速度和转向,实现直线运动和任意转弯半径的圆弧运动[7],两驱动轮轴线的中点称控制中心点。根据AGV的运动学模型,采用最优控制方法,将AGV相对导引路径的距离偏差和角度偏差同时消除到零[7]。根 据 AGV 的 机械结构和控制模型,定义AGV坐标系OAXAYA的原点OA为控制中心点在地面的投影,XA为AGV直线前进方向,YA平行于驱动轮轴线。摄像机的理想位姿是使摄像机位于控制中心点的上方且垂直于地面。图像行向量、列向量分别与XA、YA平行。摄像机这种安装方式的AGV具有测量精度高、实时性强的特性,且AGV能够双向运动。
给定一个一般空间平面与图像平面之间的单应矩阵,如果空间平面在世界坐标系的坐标已知,则该单应矩阵可以提供关于摄像机内部参数的两个线性约束。但是仅知道某一个场景中的两幅图像间的单应矩阵不能对摄像机内部参数构成任何约束[8]。由于AGV只能在地面做二维刚体运动,因此无论AGV以何种方式运动,地面参考点均在一个平面内,不能获得足够的约束以求解出所有的内部参数。标定模板与图像平面平行时的摄像机标定方法[9]必须借助辅助测量设备才能满足平行条件,不易在现场实施。
摄像机实际位姿相对理想位姿存在三个角度误差和两个平移误差,在肉眼下微调摄像机姿态能够将这些误差控制在较小的范围内。根据相机成像原理,一个不垂直于主光轴的平面视场在垂直于主光轴的成像平面上的成像会存在倾斜失真;普通镜头由于制造工艺的缺陷会形成图像径向畸变失真;成像物理平面在行列两个方向上的单位长度的像素数不一定相等,会形成图像比例失真[2]。这三种图像失真会给基于平面矢量图的视觉测量引入系统误差,因此必须建立图像失真的联合模型,对三种图像失真作图像校正。AGV坐标系的原点OA和XA方向分别作为控制策略的参照基准,也必须精确标定。

图1 AGV结构模型
2 静止状态摄像机标定及图像校正
2.1 静止状态摄像机标定
包含安装误差的摄像机实际成像模型如图2所示。设摄像机坐标系为OcXcYcZc,图像坐标系为(u,v)。根据理想透视模型有

式中,A为含有4参数的内部参数矩阵;u0、v0为摄像机的主点在图像中的像素坐标;kx、ky分别为摄像机焦距归一化后,像素相对成像平面物理坐标在u、v方向的放大系数。

图2 摄像机实际成像模型图
摄像机坐标系OcXcYcZc与世界坐标系OwXwYwZw在欧氏空间的坐标变换可以通过三维旋转矩阵和平移矩阵表示:
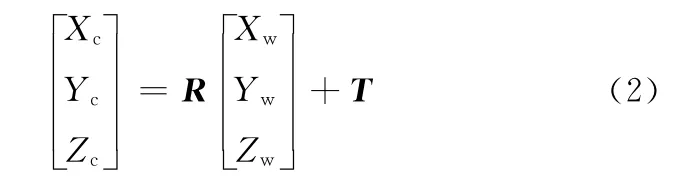
式中,R为3×3坐标旋转矩阵;T为3×1坐标平移矩阵。
一般情况下,仅仅考虑径向畸变已经足够描述由于镜头引起的非线性畸变,径向畸变关于主点是中心对称的[4]。Zhang等[10]提出的由理想坐标参数化实际坐标的模型与Tasi[11]提出的由实际坐标参数化理想坐标的模型类似,但后者在对畸变图像校正时,能够直接使用标定出的模型参数。设成像平面上的理想物理坐标为(Xu,Yu),畸变后的实际物理坐标为(Xd,Yd),采用 Tasi[11]提出的畸变参数模型,有

式中,k1、k2为径向畸变参数。
设实际像素点(u,v)经图像径向畸变校正后的像素点为(ud,vd),摄像机内部参数模型中,kx、ky分别是像素相对成像平面物理坐标在u、v方向的放大系数,由式(3)可得

要求解的模型参数包括摄像机内部参数u0、v0、kx、ky,畸变参数k1、k2和外部参数R、T。这是一个非线性最优问题,通常采用先不考虑畸变的线性模型,估计出每个参数的初值,再用最大似然估计法计算非线性模型下参数的精确值。Zhang等[10]提出的平面模板标定法比 Tasi[11]提出的三维模板标定法更易在工业现场实现,具有较高的柔性。对于平面模板坐标系,有Zw=0,令旋转矩阵 R= [r1r2r3],平移矩阵T=[txtytz]T,由式(1)、式(2)可得

式中,H为3×3单应矩阵。
将精确打印的有N个方格交点的模板以不同的姿态拍摄M 幅图像(其中一幅为模板放置在地面上),这些不同位姿的模板不在同一平面内且不是纯平动的,平面模板之间的运动参数不需要知道。采用Harris角点检测算法提取图像中方格的交点,根据图像方格交点与世界坐标系中模板真实坐标的一一对应关系,由式(5)消去Zc,每个方格点可以确定两个约束方程。因此,当N≥5时,即可采用最小二乘法计算出第i(i=1,2,…,M)幅图像对应的单应矩阵Hi。
旋转矩阵R是一个单位正交矩阵,可以建立两个约束条件[10]:

由式(6)、式(7)可以得到内部参数矩阵的两个约束方程。当M≥3时,即可采用最小二乘法计算出内部参数矩阵A的4个内部参数的初值。已知内部参数矩阵A和单应矩阵Hi,代入式(6)可以得到每幅图像对应的r1i、r2i和Ti。r3i可以由下式得到:

至此,模型参数中的u0、v0、kx、ky、Ri和Ti的初值均已得出。令畸变参数k1、k2的初值为0,在非线性模型下,采用最大似然估计法对模型参数进行优化。
对有N个方格交点的M幅图像,最大似然估计可以通过最小化距离函数获得:

其中,mij(A,k1,k2)是由式(4)获得的畸变校正后的像素点;m⌒ij(A,Ri,Ti,Mij)是由式(1)、式(2)获得的理想透视模型下世界坐标点Mij对应的理想图像坐标点。对式(9),采用基于梯度下降的非线性最小二乘最优化算法Levenberg-Marquardt,获得使函数值最小的 u0、v0、kx、ky、k1、k2、Ri和Ti的最优解。模板采集的次数越多,计算结果越精确。
2.2 图像失真校正
由视觉成像模型可知,图像相对地面真实场景存在三种失真,即径向畸变引起的畸变失真,kx与ky不相等引起的比例失真,以及摄像机主光轴不严格垂直于地面引起的倾斜失真。为了方便基于矢量图的视觉测量算法的实现,需要事先对这三种图像失真进行校正,使校正后的图像与地面真实场景成比例。畸变失真参数和比例失真参数通过摄像机标定已经确定。
设在摄像机标定中,标定模板放置在地面时,对应的外部参数为Rg和Tg,令Tg=[tgxtgytgz]T,tgx、tgy、tgz为三个坐标 轴 上 的平移分量。Rg是隐式的旋转矩阵,用欧拉角表示时,根据坐标旋转的次序有多种形式[12]。设模板所在的世界坐标系为OwXwYwZw,顺序绕Zw轴旋转γ、Yw轴旋转β、Xw轴旋转α后,与摄像机坐标系平行,即

其中,Rx(α)、Ry(β)、Rz(γ)为欧拉角旋转矩阵,它们的逆矩阵分别为自身的转置。由Rg计算α、β、γ可以参考文献[12]。
首先由式(4)对图像作径向畸变校正,得到像素点(ud,vd)。再作比例失真校正,以摄像机主点为中心,作以u轴为基准的比例拉伸,由式(1)可得

最后作倾斜失真校正,如图2所示,对图像平面分别以y、x 为转轴,作RTy(β)、RTx(α)的顺序旋转变换,令(U,V)为对三种图像失真校正后的图像,则

校正后的成像模型可以简化为

其中,s=kx/tgz为像素相对标定模板的比例因子。式(13)表明,失真校正后的图像相对地面上的平面模板是一个含有比例因子s的二维旋转平移变换。由于AGV坐标平面OAXAYA是作为控制策略的基准定义的,考虑到机械安装误差等因素,在不借助精密仪器测量的情况下,很难精确地将标定模板放置在与AGV坐标平面完全一致的位置,图像与AGV坐标平面OAXAYA满足比例因子同为s的二维旋转平移变换。因此有
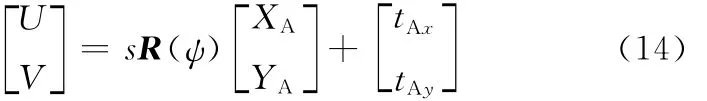
式中,ψ、tAx和tAy分别为校正后AGV坐标系OAXAYA的旋转角和两个平移分量。
解出ψ、tAx和tAy即可得到校正后的图像相对AGV坐标系的参数。
3 运动状态AGV标定
3.1 直线运动状态下的标定


式(15)表明,参考点在图像序列中的坐标呈线性分布,ψ与参考点的初始位置及AGV的速度无关,标定方法具有较好的柔性。采用最小二乘法直线拟合,如图3所示,拟合直线与图像坐标系U轴的夹角即为ψ,顺时针为正。由最小二乘法得ψ的估计为

式中,F为采集的视频帧数。
受图像随机噪声和可能存在的驱动轮滑动影响,Ut与Vt并不一定是完全线性相关的,线性相关系数r可以用来分析它们的线性相关度(理想状况下|r|=1):


图3 直线运动状态下的标定
3.2 自转状态下的标定


式中,ω为AGV的角速度;φ0、RA分别为参考点的初始位置角和到AGV坐标原点的距离。
由式(18)和式(14)可得
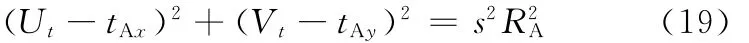
式(19)表明,参考点的像素坐标在以(tAx,tAy)为圆心、以sRA为半径的圆上,并且与参考点的初始位置角和AGV的角速度无关。对图像序列中的参考点采用最小二乘法圆弧拟合,如图4所示,拟合圆弧的圆心即为AGV坐标系相对图像坐标系的平移向量。

图4 自转状态下的标定
圆是一种非线性模型,为了便于计算,设图像坐标系下圆的方程为
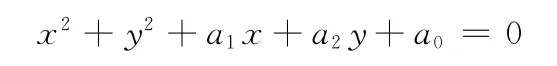
令d=-(x2+y2),e为估计误差,则估计圆弧模型参数就近似转化为二元线性回归问题:
d=a0+a1x+a2y+e

其条件是B的秩R(B)≥3,由于样本数量较大,故很容易满足。圆弧圆心坐标为

圆弧半径为

同样考虑随机噪声和可能存在的驱动轮滑动的影响,圆弧拟合均方差为

4 实验及分析

图5 标定流程图
本文采用的实验设备为维视VS-818HC工业相机(3.5~8mm手动变焦镜头VS-0358M),标定流程如图5所示。静止状态下采集不同姿态网格模板图像16幅,图像分辨率为720×576像素,采用平面模板标定法标定出摄像机的内部参数、径向畸变参数和每个模板对应的外部参数。由放置在地面的平面模板对应的外部参数计算得到摄像机相对地面的两个倾斜角和物距。通过三种图像失真校正的联合模型对图像进行校正,也确定了图像相对地面真实场景的比例因子。静止状态各参数标定结果如表1所示,大部分参数的标定均方差都在0.5%以内,ky比kx大近10%,比例失真严重。图像相对地面场景的比例因子为2.72,视觉测量精度较高。
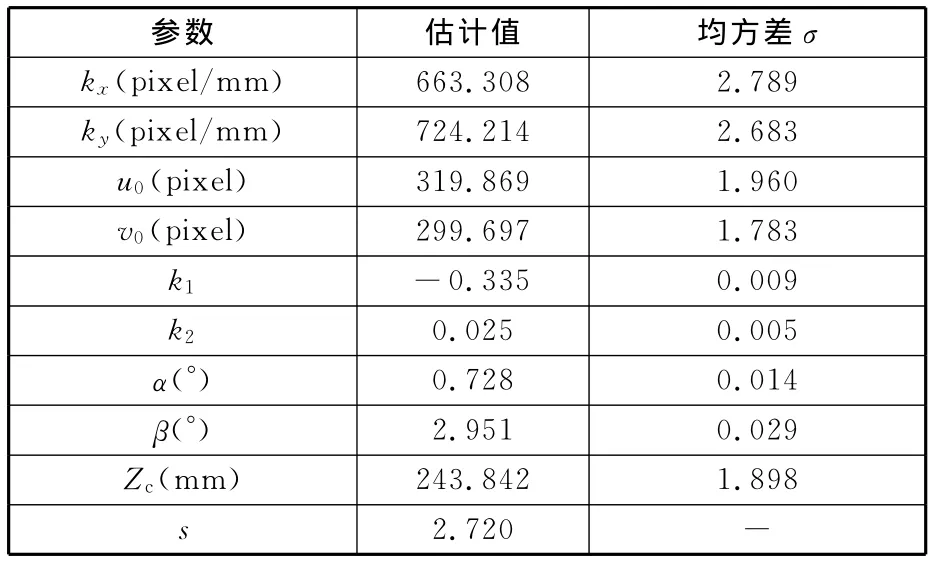
表1 静止状态参数标定
分别采集AGV匀速直线运动和原地自转视频各4次,对视频图像先进行失真校正,提取参考点在图像中的坐标,再对参考点像素序列分别采用直线和圆弧进行拟合,获得失真校正后图像坐标系相对AGV坐标系的旋转和平移参数。如表2所示,直线运动状态下参考点的线性相关性高且非常稳定,说明并没有出现非理想的滑动。如表3所示,自转运动状态下标定出的圆心坐标也非常稳定,也没有出现非理想的滑动,换算到实际物理坐标下的均方差小于1mm。
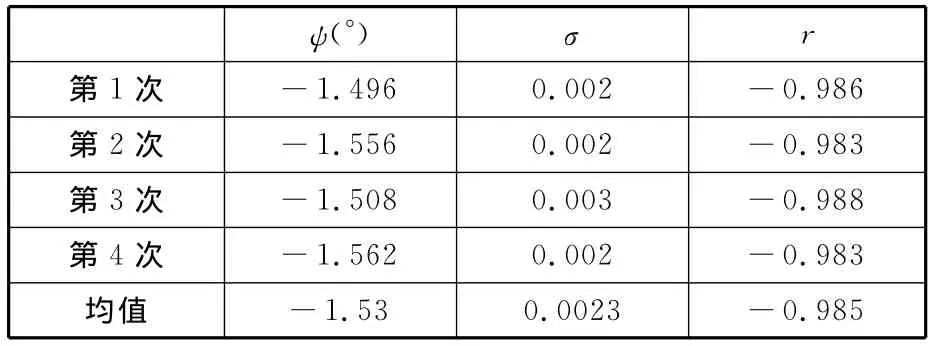
表2 直线运动状态参数标定
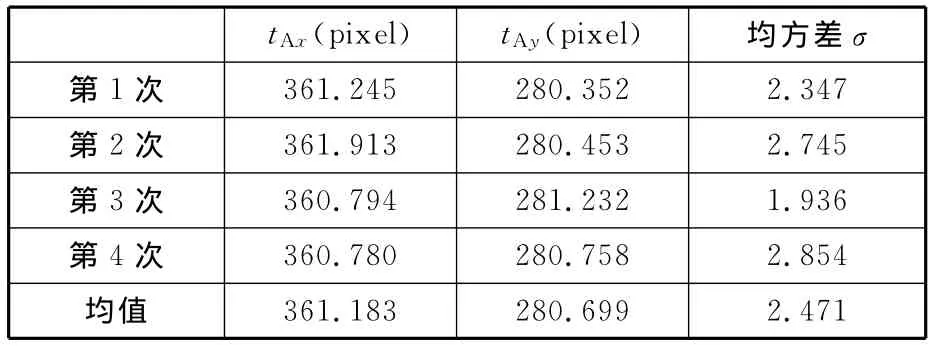
表3 自转状态参数标定
5 结论
本文提出了一种基于静止和运动两种状态的视觉导引AGV视觉标定方法,该方法能够在不借助其他辅助测量设备的条件下,精确标定出摄像机的内部参数、径向畸变参数和相对AGV控制模型坐标系的外部参数。经三种图像失真联合模型校正后的图像能够应用于基于平面矢量图的视觉测量。本文提出的现场标定方法具有柔性好、精度高、实用性强的特点。
[1]Iris F A.Vis,Survey of Research in the Design and Control of Automated Guided Vehicle Systems[J].European Journal of Operational Research,2006,170(3):677-709.
[2]Salvi J,Armangue X,Batlle J.A Comparative Re-view of Camera Calibrating Methods with Accuracy Evaluation[J].Pattern Recognition,2001,35:1617-1635.
[3]吴福朝,李华,胡占义.基于主动视觉系统的摄像机自标定方法研究[J].自动化学报,2001,27(6):752-762.
[4]Tordoff B,Murray D W.The Impact of Radial Distortion on the Self-calibration of Rotating Cameras[J].Computer Vision and Image Understanding,2004,96:17-34.
[5]王荣本,徐友春,李庆东,等.AGVS图象识别多分支路径的研究[J].中国图象图形学报,2000,8(5):632-637.
[6]Guillou E,Meneveaux D,Maisel E,et al.Using Vanishing Points for Camera Calibration and Coarse 3D Reconstruction from a Single Image[J].The Visual Computer,2000,16(7):396-410.
[7]陈无畏,李碧春,孙海涛,等.基于视觉导航的AGV模糊-最优控制研究[J].中国机械工程,2006,17(24):2546-2550.
[8]孙凤梅,胡占义.平面单应矩阵对摄像机内参数约束的一些性质[J].计算机辅助设计与图形学学报,2007,19(5):647-650.
[9]罗晨,朱利民,丁汉.标定模板与图像平面平行时的摄像机标定方法[J].中国机械工程,2006,17(16):1558-1561.
[10]Zhang Zhengyou.Flexible Camera Calibration by Viewing a Plane from Unknown Orientations[C]//Proceedings of the 1999 7th IEEE Int.Conference on Computer Vision(ICCV’99).Kerkyra,1999:666-673.
[11]Tsai Y.A Versatile Camera Calibration Technique for High-accuracy 3DMachine Vision Metrology Using Off-the Shelf TV Cameras and Lenses[J].IEEE Int.J.Robot.Automat.,1987,3:323-344.
[12]Diebel J.Representing Attitude:Euler Angles,Unit Quaternions,and Rotation Vectors[M].Stanford:Stanford University,2006.
