一种基于时域响应的预测控制算法的研究
2012-12-01蒋存波张淑祯陈俊达苏柱宾
蒋存波 张淑祯 陈俊达 苏柱宾
(桂林理工大学信息科学与工程学院1,广西 桂林 541004;桂林理工大学机械与控制工程学院2,广西 桂林 541004)
0 引言
工业控制过程中,许多系统具有大滞后这一特性,运用传统的控制方法很难获得满意的控制效果。预测控制是一种在工业实践过程中逐步发展起来的计算机控制算法[1]。该算法采用有限优化窗口,大大减少了优化计算量;采用滚动策略,在局部优化的基础上实现了全局优化;利用反馈校正,解决了系统干扰等不确定问题[2]。本文提出的基本思想是利用当前和以往的采样信息,以及在此前已经输出的控制信息,预测滞后N点之后系统的响应输出;同时按照一定的性能指标,构造当前采样时刻的控制器输出信号,使系统的性能指标最优。
1 预测控制的基本算法
预测控制是一种基于模型的多变量的控制算法,其基本原理可以从预测控制算法的三个要素——模型预测、滚动优化和反馈校正中体现出来[3]。预测控制算法的基本思路是通过对控制系统历史行为的评估,实现对被控对象未来输出的预测,从而预先采取一系列措施,使被控对象的输出尽可能沿着设定的轨迹进行调整。预测控制器原理框图如图1所示。

图1 预测控制器原理框图Fig.1 Principle of the predictive controller
图1中:GC(s)为预测控制调节器传递函数;r为系统给定值;e为偏差信号;e=r-y;u为控制器的输出控制信号;G(s)为包含实行机构在内的广义被控对象的传递函数;y为系统输出。
调节器GC(s)对偏差e按所选择的控制算法进行运算,产生的控制信号u通过执行机构作用于被控对象G(s),使系统的输出信号y满足控制指标要求[4]。预测控制器的设计目的是利用当前及之前的激励和响应来预测今后某时刻系统的响应,以便预先采取适当的控制,使系统在该控制信号产生控制作用时能够满足控制要求。
本文针对具有一阶滞后特性的系统进行预测控制算法的研究,以具有此特性的电加热系统为试验对象,完成了预测控制算法的推导和仿真测试。电加热系统执行环节为可控硅调功器(silicon controlled rectifier,SCR),由于执行环节的惯性和滞后时间远小于被控对象的惯性时间和滞后时间,故可将其看作一个增益为k2的比例环节[5-6]。电加热驱动器与被控对象如图2所示。

图2 电加热驱动器与被控对象示意图Fig.2 Electric heating driver and the controlled object
图2中:k2为执行环节的增益;GO(s)为被控对象的传递函数;kO为被控对象的比例系数;θ为惯性时间常数;τ为滞后时间。

式中:k=k2kO。
对于计算机控制系统,当选择采样周期T=τ/N(或者N=τ/T)时,由于系统的滞后特性,第n个采样周期产生的控制信号U(n)需要滞后N拍才影响输出,而第n个采样周期对系统产生作用的为U(n-N)。从第n个采样时刻开始,激励信号由第(n-1)采样时刻的U(n-N-1)变为第n个周期的U(n-N),系统进入一个新的过渡过程。这个新过渡过程的初始条件为采样值Y(n),稳态值为kU(n-N),它的时域响应可用下式描述:
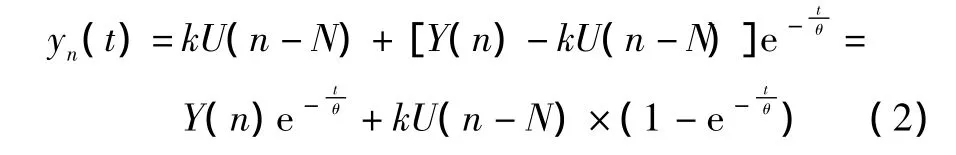
式(2)描述的过渡过程实际只经历一个采样周期时间t=T,就进入第(n+1)个采样时刻,第(n+1)个采样值Y(n+1)就是式(2)描述的yn(t)在t=T时刻的值yn(T)。在第(n+1)周期,激励信号由第n周期的U(n-N)变为U(n-N+1),而 Y(n+1)=yn(T),系统又进入一个新的过渡过程。计算机控制系统通过在每一个采样周期施加所需要的控制信号U(·),不断调整各采样周期的过渡过程响应曲线yn(t),使系统的总响应y(t)满足对性能指标的要求。本文的目的是利用已产生的但还未起作用的控制信号U(n-N+1)~U(n-1)和系统的特性来预测系统在当前采样点后y(t)的变化过程,从而确定第n个采样周期的控制信号U(n),使系统经过U(n)的作用在第(n+N)周期结束时,系统偏差E(n+N)=r-yn+N(T)=r-Y(n+N+1)趋于零。
为了在第n个采样时刻求出使系统在第(n+N)个周期的偏差E(n+N)=r-Y(n+N+1)=0的控制信号U(n),需要对系统在第(n+1)~(n+N)采样周期的输出进行预测,以获得系统在第(n+1)~(n+N)之间的采样信息的预测值。第(n+1)采样时刻的输出值就是式(2)中t=T时的值,故系统在第(n+1)采样时刻输出的预测值为:

第(n+1)周期的激励为U(n-N+1),输出函数为:
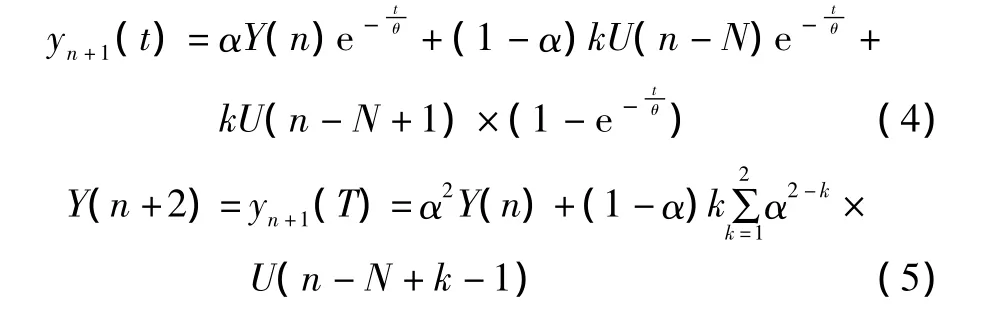
第(n+m)个采样周期时的输出为:

式中:Y(n+m+1)为yn+m(t)在t=T时的值。
令m=N,可以得到:
1947年,吴努提出为了防止外来侵略,缅甸需要寻找好的盟友时,也告诫说盟友一旦找错,那会比外来侵略者更危险。[41]英国、美国上述给缅甸带来的这种不信任和经济军事援助诉求的落差,部分印证了缅甸人的这种担心,反向增加了缅甸同中国、苏联保持友好关系的动力。

对于阶跃输入信号r,偏差信号为:

通过U(n)的调整作用,使得系统在第(n+N)个采样周期结束时输出与期望值r的偏差为0。利用式(7)和式(8)可推导出满足该要求的控制信号U(n)为:

应用式(9)进行预测控制,可以依据被控对象参数(对象的滞后时间τ、惯性时间常数θ、增益系数k=k2k0)和采样周期T来确定式(9)中的三个参数(N、α和k)的值,或者通过试验方法确定N、α和k;另外还可以使用文献[7]介绍的方法,利用当前采样点及其以前(N-1)点的采样信息,通过在线参数辨识方法获取对象的相关参数,并在线计算N、α和k值。
下文具体介绍控制算法的试验测试过程。
2 控制算法试验测试
2.1 仿真方法
以具有大滞后特性的一阶大惯性系统为被控对象,用Matlab仿真研究在阶跃输入下预测控制算法时系统的控制性能,以及对象参数变化对控制性能的影响程度,从而评估预测控制算法在一阶大惯性大滞后对象控制过程中的有效性[8-9]。取采样周期T=0.1 s,仿真过程中,被控对象采用差分方程进行描述,即:

式中:Y(n)为系统输出响应;k2为执行装置的增益,kO为被控对象的增益系数,k2、kO∈[0.1 ~30];U(n -N)为控制器的输出控制信号;惯性时间θ取值区间为1~1000s;系统滞后时间τ的取值范围为1~500s。
在实际系统中,实际温度的测量值在系统理想输出Y(n)的基础上叠加了噪声ε(n),用YC(n)表示采样(或叫测量)值,即YC(n)=Y(n)+ε(n)。仿真时,利用一个Randn随机函数作为噪声源ε(n)。为了减少干扰和测量噪声的影响,对测量值YC(n)进行递推平均值滤波[10],其数学表达式如下:

式中:YT(n)为经过滤波处理后的第n个采样信号;YC(n)为第n个采样信号;YT(n-i)(i=1~7)为前7个采样点经过滤波的采样信号。
2.2 仿真结果
当阶跃激励信号r=200、采样周期T=0.1 s时,对已知参数的被控对象,可利用该预测控制算法进行控制,获得的控制性能仿真试验结果如图3所示。
图3(a)中,对象滞后时间变化导致响应曲线在时间轴上平移,系统增益系数和惯性时间变化仅影响曲线的上升时间,增大系统增益k(主要是增大执行机构的增益k2)可以缩短上升时间。因此,无噪声时式(9)描述的预测控制具有理想的控制效果。
图3(b)中的曲线①为利用有噪测量信号进行预测控制的结果,曲线②为加入了噪声的测量信号。由于受测量噪声的影响,输出出现明显的波动。
图3(c)中的曲线②是在有噪声情况下经过递推平均值滤波算法处理后的测量信号,对应的曲线①是利用滤波后的测量值进行预测控制的响应曲线。
式(9)描述的预测控制算法中的α、N和k由被控对象参数(θ、τ和总增益k)值确定,这表明对象参数变化对预测控制效果可能会产生影响。利用在运行过程中分别改变(增大或减小)被控对象参数值而获得的仿真曲线来研究这些参数变化对预测控制效果的影响,如图3(d)和3(e)所示。系统滞后时间改变后输出产生小幅波动,经过短暂时间后系统又恢复稳定,说明滞后时间τ的变化对预测控制效果影响不大。
图3(e)反映的是对象惯性时间常数θ和增益k分别变化时对预测控制效果的影响。曲线①和曲线②是不同设定值时,惯性时间增大到原来的2倍和减小到1/2时系统的响应曲线。在参数发生变化时,输出产生波动,但很快恢复稳定。图3(e)中的曲线①和曲线②结合图3(a)表明了惯性时间常数除影响上升时间和引起短暂波动外,对稳态特性基本没有影响。图3(e)中曲线③和曲线④是增益变化的响应曲线。
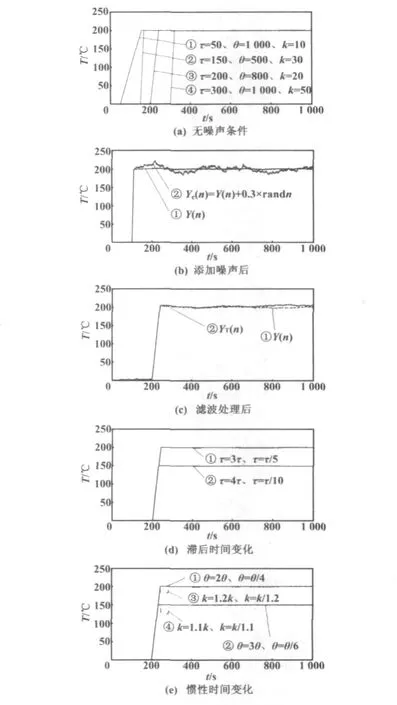
图3 预测算法仿真测试曲线Fig.3 The simulation curves of prediction algorithm
通过仿真测试,表明式(9)描述的预测控制算法具有较理想的控制效果。在稳定运行状态下,对象滞后时间和惯性时间常数变化对响应有轻度影响,但输出会很快恢复。增益在±20%内变化时,系统将出现短时超差且能恢复,但过大的增益变化会导致性能变差甚至导致系统无法稳定运行。通过调整预测算法中的系数k,可以适应对象的增益变化,利用滑动平均值滤波,可减小测量噪声对控制性能的影响。
3 结束语
本文提出的基于时域的预测控制算法,对具有大滞后特性的一阶系统具有较好的阶跃响应性能。纯滞后时间和惯性时间常数变化对闭环系统响应曲线的滞后特性和上升时间有影响,但对系统的稳态控制性能和超调量影响小。这表明该控制算法对被控对象惯性时间常数和滞后时间的变化有较好的适应性。对象增益变化对控制性能有较大影响,当增益变化不超过±20%时,输出虽出现较大幅度波动,但能较快恢复稳定。增益变化过大时输出将难以恢复稳定运行,通过调整预测控制算法中的系数k,就能较方便地适应对象增益的变化。
仿真试验表明,该预测控制方法控制性能良好、计算简单、鲁棒性强、抑制干扰能力好。该算法针对已知参数的一阶滞后对象进行推导和试验,对于二阶对象或未知参数的控制系统的实现有待进一步探讨研究,预计在工业控制领域将会有较好的应用前景。
[1]雌刚,韦红旗,陈绍炳,等.单元机组负荷多变量模型预测控制[J].中国电机工程学报,2002,22(4):144 -148.
[2]吴建国,张培建.基于预测函数控制的纯滞后系统的研究[J].自动化仪表,2004,25(11):8 -10.
[3]赵丹丹,梁平.非线性预测控制在电厂热工过程中的应用研究[J].广东电力,2009,22(1):2 -7.
[4]徐爱微.模糊预测控制技术在大滞后温度系统中的应用研究[D].北京:中国计量科学研究院,2007.
[5]蒋存波,张淑祯,覃彦芝.一种单参数PID控制算法参数整定方法研究[J].自动化与仪表,2010,31(7):32 -34.
[6]穆珊珊,肖维荣.广义预测控制隐式算法在温控系统中的应用[J].自动化仪表,2009,30(5):43 -45.
[7]蒋存波,刘丽.一种温度对象参数辨识方法及仿真研究[J].科学技术与工程,2009,9(11):3105 -3108.
[8]王国玉,韩璞,王东风.预测函数控制及其应用研究[J].系统仿真学报,2002,14(8):1087 -1091.
[9]张培建,吴建国.基于特征模型的预测函数控制的仿真研究[J].系统仿真学报,2008,20(10):2646 -2649.
[10]张玉珊,崔金玲.数据采集系统中的数字滤波方法研究[J].河南机电高等专科学校学报,2007,15(3):23-24.
