时栅位移传感器的误差分离与补偿方法研究

彭东林 孙世政 高忠华 陈锡侯 杨继森 郑方燕

(重庆理工大学机械检测技术与装备教育部工程研究中心，重庆 400054)

0 引言

时栅传感器是一种全新的位移传感器［1－2］，它实现了以时间测量空间的功能。但由于温度漂移、电子元器件的不稳定性、机械加工误差等各种不确定因素的存在，影响了时栅精度的进一步提高。时栅传感器的误差产生具有一定的规律性和确定性，因此，可以通过补偿方法对误差加以消除或抑制［3－5］。误差分离补偿技术在测角系统中被广泛采用，本研究试图通过分析时栅传感器测角系统的误差组成，研究误差的分离方法和基于最小二乘法的误差补偿方法，从而大幅度提高时栅角位移的测量精度。分离为n次误差谐波的叠加之和［6］。因此，运用傅里叶级数分离法，测角系统的误差公式可表示为:

式中:Δδ为测角系统的误差;n为误差展开为傅里叶级数的次数;α为时栅测量系统所测量的角度值。

由式(1)可以看出，傅里叶变换的实质是将Δδ这个波形分解成许多不同频率的正弦波的叠加［4－6］。此时系统的综合误差与傅里叶级数是一致的，分离误差可以直接采集若干位置的对应误差;然后进行傅里叶变换，通过式(1)，即可得出误差的规律;最后对测量误差进行补偿。

1 时栅测量系统的误差分离

2 误差补偿的实现

傅里叶变换被大量使用在工程中，尤其是应用在旋转机械设备的故障诊断和误差分析过程中。时栅角位移测量系统的误差可被视为是n次误差谐波的叠加，而按照傅里叶变换的思想，可以将测量系统的误差

2.1 补偿模型的建立

最小二乘法是一种广泛应用在多学科领域中的数据处理方法，它既可用于线性参数的处理，又可用于非线性参数的处理。

由于测量数据不可避免地包含测量误差，所以为了提高所得结果的精度，应适当增加测量次数，从而利用抵偿性减少随机误差的影响。将式(1)写成矩阵的形式，则有:

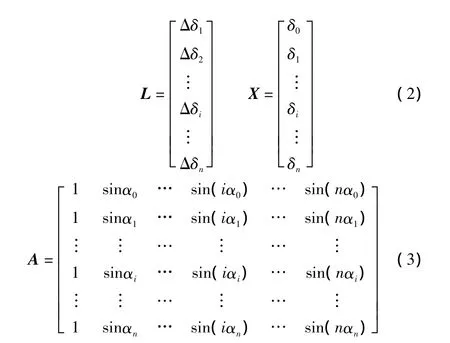
根据最小二乘法原理，测量结果的最可信赖值应在残余误差平方和最小的条件下求出，故引入残余平方和矩阵V(V=L－AX)。在等精度测量时，残余误差平方和VTV为最小的条件即(L－AX)T(L－AX)为最小［7－8］。

2.2 最小二乘法的实现

将式(1)转换为矩阵形式L=AX，则可视为将误差的非线性转换为线性，然后运用拟合的方法，采用n次谐波来逼近反非线性曲线。矩阵A在谐波次数为n和采样点个数确定的情况下可以通过计算求得，而矩阵L中的基准误差可以通过光栅测量得到。根据最小二乘法原理，在残差平方和VTV最小的条件下，可以求解出矩阵X，从而得出误差的曲线规律。采样点数量的选择由拟合的谐波次数决定，在谐波次数一定的情况下，采样点要大于未知数的个数。采样点越多，拟合的曲线就越接近真实情况。

3 软件实现

误差补偿算法流程如图1所示。

图1 算法流程图Fig.1 Flowchart of algorithm

本文采用Matlab7.1编程软件，在系统的误差补偿中采用的是软件补偿的方法，具体包括取测量角度和谐波次数的初始值、各次谐波的计算、残差平方和的计算以及参数计算等模块。

运用该方法进行误差分离时，需根据经验或已测得的数据判断测量系统误差的主要成分，即要先确定最高次谐波的谐波次数n，并在残差平方和为最小的条件下求出方程中的未知量，进而对误差规律进行拟合。该方法能够较快地找到误差的可信规律，其最终结果能充分利用误差的抵偿作用，从而有效减少随机误差的影响，具有可信赖性［9－11］。通过对时栅传感器误差曲线进行修正，使时栅传感器的测量精度得到进一步提高。

4 试验与测试实例

时栅传感器误差的测量是以高精度光栅作为角度测量的基准。将光栅和时栅传感器分别通过弹性联轴结安装在精密分度转台的主轴上，随转台同时转动。伺服电机通过同步带轮带动转台做匀速转动的同时，也使光栅和时栅同时转过相应的角位移，每转动一个位置，分别读取光栅和时栅测量所得的角度值，两者的差值就是时栅测角系统的原始误差。本研究中用于测试的时栅传感器选用海德汉公司生产的光栅，其型号为TGS132F型。该光栅的测量精度可达到±1″。试验过程中，在整周360°内共测试了720个位置点，部分采样点数据如表1所示。以第一组数据为例，它表示的是将转台转过固定角度，当时栅测量的角度值为0°00'00″时，光栅测量的角度值为 0°00'03″4，它们存在的误差值为 －3.1″。

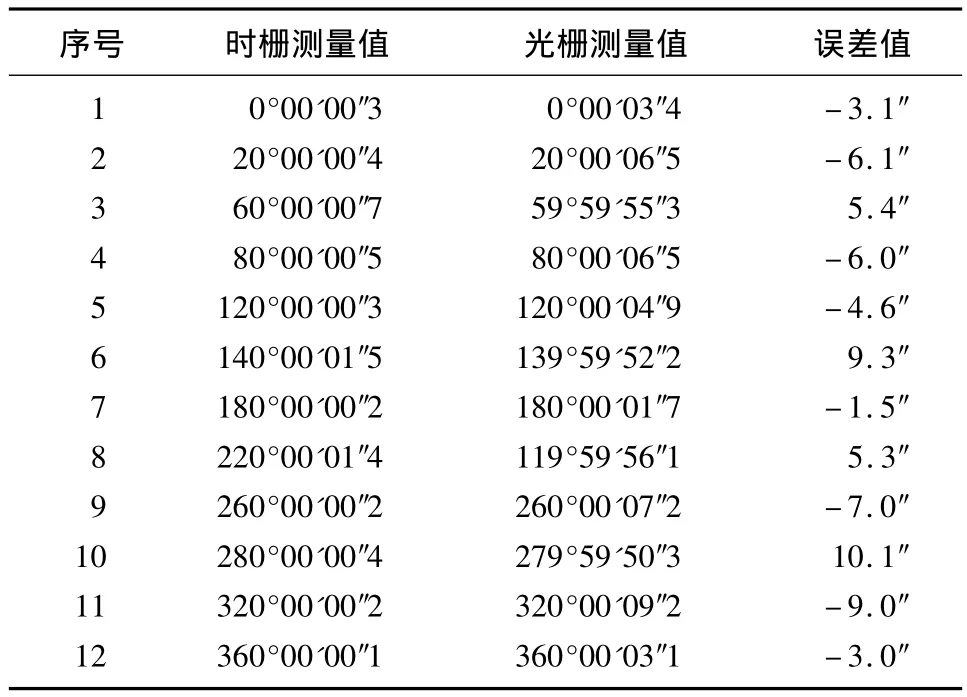
表1 部分采样点数据表Tab.1 Partial data sample data

对应的空间角度测量误差曲线，即未修正的测量误差曲线如图2所示。

图2 未修正的测量误差曲线Fig.2 The error curve before correction

试验证明，时栅角位移测量系统的测量误差的主要成分是低次谐波误差。当选取谐波次数n=10时，拟合的误差规律曲线与实际的误差曲线拟合度最好。对所得的拟合误差曲线再进行误差补偿，得到的曲线如图3所示。

从图2和图3可以明显看出，补偿前后误差范围从 ±10.2″降到 ± 2.1″，误差修正的结果说明该补偿方法对本系统起到了很好的误差补偿作用。

5 结束语

本文针对时栅角位移测量系统中的误差特性进行分析，提出了基于最小二乘法的误差分离和补偿模型，并运用该模型对使用的时栅测角系统进行误差补偿。在实际的传感器生产过程中［12－13］，通过运用软件对时栅角位移测量系统中存在的误差进行补偿，有效地节约了生产成本和生产时间，并在一定程度上提高了时栅角位移测量系统的测量精度。

［1］彭东林.时栅位移传感器与新型机床动态检测系统［M］.北京:科学出版社，2010:56－69.

［2］彭东林，张兴红，刘小康，等.场式时栅位移传感器研究［J］.仪器仪表学报，2003，24(3):321 －323.

［3］陈自然，彭东林，王先全，等.基于Matlab的时栅位移传感器的误差曲线分析与拟合研究［J］.工具技术，2008，42(12):85 －88.

［4］张天恒，彭东林，杨伟，等.时栅传感器电气误差分析及补偿［J］.工具技术，2009，43(8):107 －109.

［5］彭东林，刘小康，张兴红，等.高精度时栅位移传感器研究［J］.机械工程学报，2005，41(12):126 －128.

［6］冷建华.傅里叶变换［M］.北京:清华大学出版社，2004:15－26.

［7］费业泰.误差理论与数据处理［M］.5版.北京:机械工业出版社，2004:94－98.

［8］费业泰，陈晓怀.精密测试及仪器的误差修正技术［J］.宇航计测技术，2006，16(4－5):66－70.

［9］李金海.误差理论与测量不确定度评定［M］.北京:中国计量出版社，2003:1－59.

［10］谭久彬.精密测量中的误差补偿技术［M］.哈尔滨:哈尔滨工业大学出版社，1995:18－20.

［11］李秋明，冯汝鹏，王景贺，等.感应同步器测角系统误差分析及补偿［J］.中国惯性技术学报，1998，6(1):50 －54.

［12］张星，白强，夏善红，等.小型三维电场传感器设计与测试［J］.电子与信息学报，2007，29(4):1003 －1004.

［13］唐海，行鸿彦，季鑫源.大气电场仪中相敏检波器的分析设计［J］.现代电子技术，2009，30(13):8－10.