三相直流电机伺服系统设计
2012-12-01陈志佳孙书鹰张炜栋
陈志佳 孙书鹰 张炜栋
(军械工程学院光学与电子工程系1,河北 石家庄 050003;92151部队2,山东 青岛 276825)
0 引言
2007年6月,意法半导体公司推出了一款基于Cortex-M3内核的新型32位 ARM处理器,即STM32F103嵌入式微处理器。该款处理器无论在数据处理速度方面还是控制性能方面,都能很好地满足伺服控制系统的要求。STM32F103对片上外围设备进行了改进,内嵌了适合三相无刷电机控制的定时器和ADC。其高级PWM定时器可提供6路带死区的PWM输出,PWM定时器可使用72 MHz时钟输入;其中任何一个GPIO均可映像到外部中断,GPIO的最大翻转频率可达18 MHz[1]。该款处理器的指令执行速度非常快,每秒可执行1.25×106条指令,再结合其高速数据处理能力,STM32F103能够很好地支持控制算法,实现实时、高精度控制。
在电机选型方面,采用带有星型齿轮减速装置的三相直流无刷电机,以霍尔元件作为换向传感器,通过控制器实现换向。霍尔传感器输出信号除了起到换向作用外,还可用作位置和速度传感器,从而简化了位置和速度检测电路,并在保证精度的前提下降低费用,从而提高性价比。
1 伺服系统整体设计
三相直流电机伺服系统主要由位置传感器、STM32F103嵌入式微处理器及其外围设备、电机驱动器、伺服和位置检测电路组成,系统整体结构如图1所示。
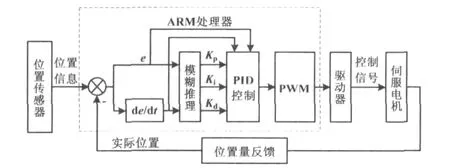
图1 系统整体结构图Fig.1 Overall structure of system
位置传感器由PC机通过串口提供角度信号,模拟实际火控系统向被控火力系统提供射击诸元(方位角或射角),并将该位置信息通过串行口发送到STM32F103微处理器。对微处理器综合接收到的位置信息与从伺服电机反馈回来的位置信息进行相减运算,得到位置误差信号e。ec为误差的变化,在微处理器中作为e的差分信号。在火力系统跟踪过程中,微处理器不断检测e和ec,根据e和ec,对比例系数Kp、微分系数Ki和积分系数Kd进行在线修改,同时根据增量PID控制的原理,利用参数Kp、Ki和Kd得到误差控制量。随后微处理器根据误差控制量,计算得到PWM波形占空比控制信号,并控制输出至直流电机驱动器的电压,进而改变电机转速和转向等,从而达到火力系统实时跟踪火控系统给定诸元的目的。
2 控制电路设计
2.1 驱动器及应用
本设计采用ZHauto WS-2406三相无刷电机驱动器,驱动器及其端口连接如图2所示。

图2 驱动器及其端口连接示意图Fig.2 Connections of the driver and its ports
除电源外,该驱动器端口共有三类信号,即三相电机动力驱动信号、三相霍尔换向信号和电机状态控制信号。各端口信号的功能具体如下。
①三相电机驱动信号U、V和W为三相无刷电机提供相位互差120°的方波电流,产生电磁转矩,驱动电机转动。
②三相霍尔换向信号A、B和C是电机霍尔传感器产生的三相换向输出信号,三相之间各差120°。在本设计中,利用该信号检测电机转角和转速。
③电机状态控制信号分为转向控制信号CW/CCW、转速控制信号DA和电机制动信号BRK。其中,CW/CCW为数字信号,且低电平有效,由微处理器的PC5和PC6端口对其控制。DA为模拟信号,输入电压为0~+5 V,调节此处电压即可调节电机转速,由微处理器输出的PWM信号经积分后产生0~+5 V模拟信号,用来控制电机转速。BRK为数字信号,设计时将其与微处理器的PC7端口连接,实现制动控制。
2.2 转角与转速测量原理
三相无刷电机的三相霍尔传感器输出信号与电机的转角之间具有严格的对应关系[2]。在一个周期(360°)内,霍尔传感器输出的三相方波电压波形A、B、C三相换向信号可以分为六个区间,在每个区间对该三相信号进行编码,可得到一个周期内的信号编码为 010、011、001、101、100、110。该编码为三位循环码,由此可以判断电机转轴角度所在区间,角度分辨率为60°。如果电机是四个极对数,则角度分辨率为30°,这样就可实现计数式测角。由于对角度量进行微分可以得到速度量,因此,微处理器将采集到的角度值进行差分处理就可得到电机的转速。
由上述分析可以看出,三相霍尔传感器输出信号可以作为计数式角度传感器,经数据处理后得到角度的变化率,实现测速发电机的功能。同时,由于霍尔传感器与电机转轴为刚性连接,因此不仅可以利用其替代角度传感器和测速发电机,而且不存在机械传动链的空回和延迟等问题。但是,由于角度分辨率较低,设计中采用的四个极对数电机的分辨率只能达到30°,因此,无论是测角还是测速必然会出现较大的阶梯误差。为解决这一问题,本系统选用较大的机械传动比,使电机与被控对象之间存在较大转速差,即电机通常工作在高速状态,其对应的实际角度分辨率因此得以提高。设计中采用210∶1的星型机械传动链,其实际角度分辨率的表达式为:

式中:r为实际角度分辨率;R为电机角度分辨率;Ω为电机转速;ω为被控对象转速。
被控对象角度分辨率为:

该角度值换算成角密位为0.143×16.6666=2.38密位,可以满足火控系统跟踪系统对角度分辨率的要求。
2.3 角度编码提取电路设计
A、B、C三相信号编码为循环码,每次只有一相信号发生翻转。微处理器对此翻转信号产生的中断进行计数,实现角度检测功能。为统一触发中断信号形式,将所有跳变统一变换为窄脉冲。在此采用可重触发的双单稳态集成芯片74LS123予以实现。该芯片的触发方式有上升沿触发和下降沿触发两种。由于每个74LS123芯片有两个触发器单元,每相用一片,一个检测低变高跳变,另一个检测高变低跳变。三相共用三片74LS123,其6个触发器单元由Q端输出并接OC门反相器,各OC门的反相输出连接在一起进行上拉形成线或。位置检测电路及脉冲信号示意图如图3所示。
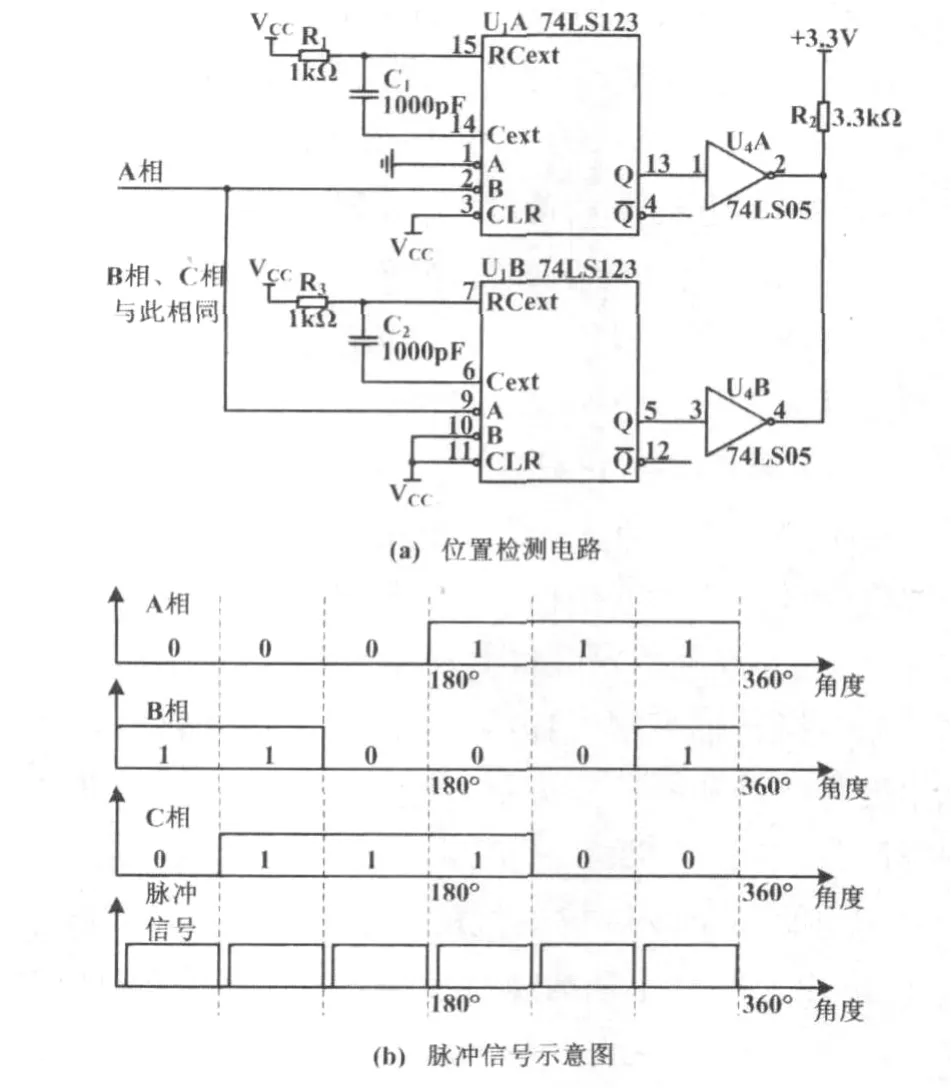
图3 位置检测电路与脉冲信号示意图Fig.3 Pulse signal schematic and circuit of position detection
3 模糊PID控制器设计
PID控制具有原理简单、鲁棒性强等优点,但也存在着非线性、时变以及参数在线调整困难等问题,在实际应用中有其局限性;而模糊控制则可以很好地解决上述问题,因而被广泛应用于模型不确定、非线性和参数时变的控制过程中[3],但普通的模糊控制稳态精度较低。因此,考虑采用模糊PID控制,充分发挥二者优点,从而达到较好的控制效果[4]。
3.1 模糊控制的实现
模糊控制器主要包括模糊化接口、知识库、模糊推理机和解模糊接口四部分[5]。本模型采用二输入三输出结构,其组成如图4所示。控制器的输入经过模糊化接口后,由精确量转变为模糊量;由数据库和规则库构成的知识库为模糊推理提供数据和推理规则;经过模糊推理后,解模糊即可输出精确数字量。
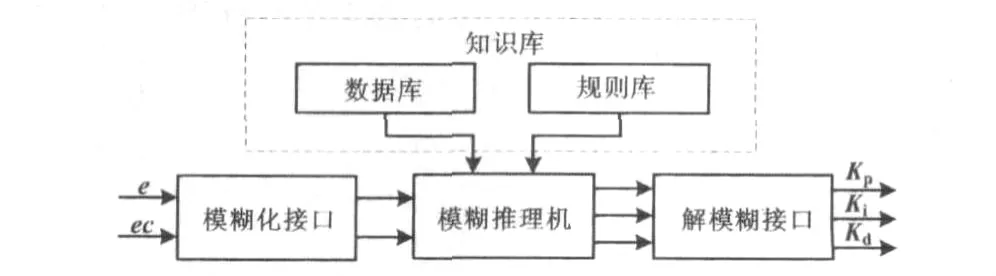
图4 模糊控制器组成框图Fig.4 Composition of fuzzy controller
3.1.1 输入输出变量的模糊化
模糊控制器以误差e和误差变化率ec作为输入,以Kp、Ki和 Kd作为输出,其中 e和 ec都是连续变量。试验得到e的基本论域为[-5,5],ec的基本论域为[-6,6]。将 e、ec 以及 Kp、Ki和 Kd变换到模糊论域E={-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}上,对应子集为{NB,NM,NS,ZO,PS,PM,PB},其表示的含义为{负大,负中,负小,零,正小,正中,正大}。
3.1.2 模糊控制规则的建立
根据对已有直流伺服系统设计经验的总结,可以得出以下三条 PID控制器参数 Kp、Ki和 Kd的规律[6-7]。①当|e|较大时,为迅速减小误差,应选取较大的Kp。同时为避免误差瞬间变大可能引起的微分过饱和,应取取较小的Kd。为防止出现较大的超调,需要限制积分作用,通常选取较小的Ki。②当|e|和|ec|处于中等大小时,为使系统响应具有较小超调,应选取较小的Kp,而Ki和Kd取值要适中。③当|e|较小时,为使系统提高精度,不产生振荡,应该选取较小的Kp和较大的Ki。Kd的值根据ec大小决定,当ec较大时,Kd取较小值。根据上述基本原则和试验中的经验得到模糊控制规则表如表1所示。
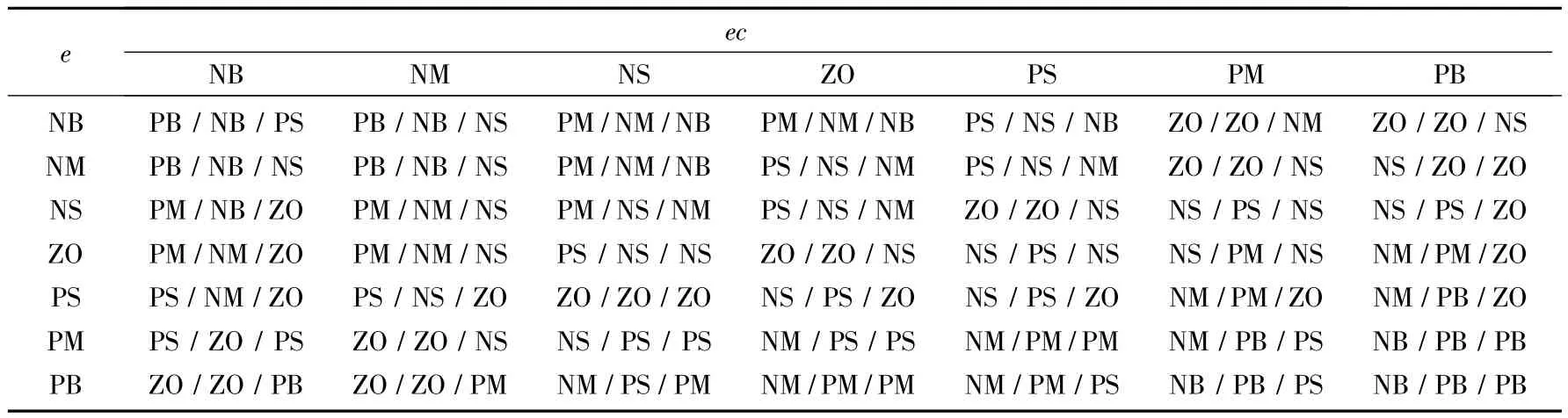
表1 Kp、Ki和Kd的模糊控制规则表Tab.1 Fuzzy control rules of Kp、Kiand Kd
3.1.3 解模糊
由模糊控制规则得到的推理结果为模糊值,不能直接用作被控对象的控制量,而是需要将其转换为微处理器可以识别的精确量。这里输入输出量均采用三角形隶属度函数,利用查表法解模糊即可得出精确的、适合微处理器运算所需的数字量[8]。
3.2 模糊PID控制的软件实现
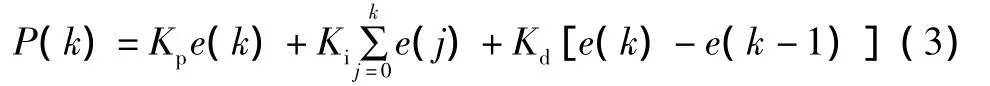
根据PID控制的定义,输入与输出的关系为:式中:Kp、Ki和Kd均由模糊推理得到。要计算P(k),不仅需要得到本次偏差信号e(k)与上次的偏差信号e(k-1),还需要对以前的历次偏差信号e(j)作累加。这将增大微处理器计算量,在实际应用中是不合适的。
为解决上述问题,可假设P(k-1)的表达式为:
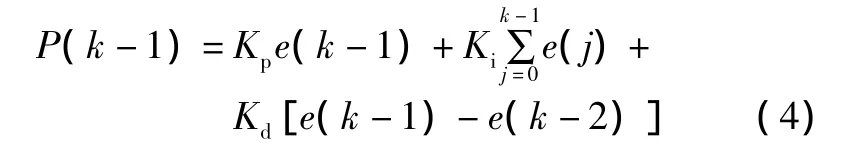
将式(3)与式(4)相减,可得增量型 PID算式为[9]:
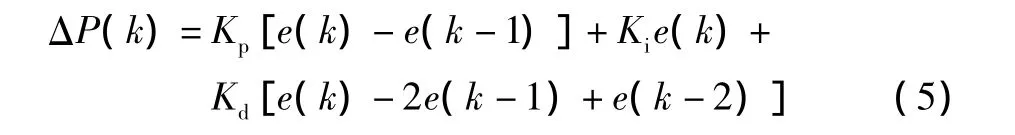
由式(5)可知,ΔP(k)仅与 e(k)、e(k-1)和 e(k-2)有关。
在PID控制过程中,当误差e较大时,由于积分的作用会产生超调量,严重时甚至会导致系统振荡。因此,需采取积分分离的措施。在偏差量较大时,将积分系数Ki置为0,只有当偏差降低到一定值后,才将积分作用引入[10]。
本设计中的临界值取5,表达式如式(6)所示:
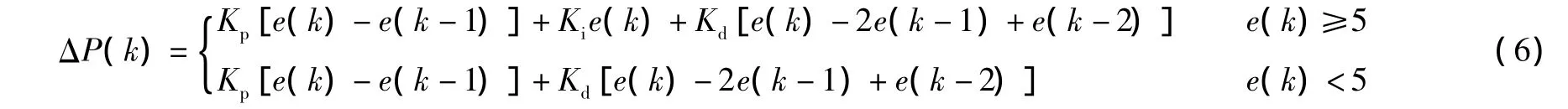
根据上述计算,得到模糊PID控制流程图如图5所示。

图5 模糊PID控制流程图Fig.5 Process of fuzzy PID control
4 试验与结果分析
在测试试验中,由PC机代替位置传感器,根据模拟飞行航路,计算并输出火力系统射击诸元(“射击诸元”是指火炮射击时装定的数据的总称,包括高低角、方位角等信息),并将这些值通过串口发送至微处理器STM32F103。微处理器控制伺服电机转动,实现模拟跟踪,在此期间不断向PC机发送当前伺服系统的位置信息,并最终在PC机号加以显示,用于测试跟踪精度和速度。
模拟航路跟踪及其误差曲线如图6所示。

图6 模拟航路跟踪与误差曲线Fig.6 Simulated route tracking and error curve
由以上分析可知,跟踪误差主要由角度传感器产生。如果需要提高系统精度,可以通过提高传动比或采用单独的高精度角度传感器加以实现。
5 结束语
本设计的直流电机伺服系统以新型ARM处理器STM32F103为核心构建。在软件设计方面充分利用了该款微处理器指令和数据处理速度快的优势,采用增量型积分分离式数字PID控制与模糊控制结合的控制策略,提高了跟踪精度;在硬件电路设计方面,处理器的PWM输出并没有直接用于电机控制,而是经过积分后输入到三相直流电机驱动器,实现对电机的控制。经调试试验,系统基本达到了硬件电路所能达到的最小误差,具有较好的实时性,基本达到了火控系统某实验演示系统的要求。
[1]李宁.基于MDK的STM32处理器开发应用[M].北京:北京航空航天大学出版社,2008.
[2]栾亚群,程婷,赵一洁.基于ATmega48的三相无刷电机控制方法[J].国外电子元器件,2008,16(11):38 -42.
[3]诸静.模糊控制理论与系统原理[M].北京:机械工业出版社,2005.
[4]吕矿生,周杏鹏,陶连斌,等.基于模糊PID的雷蒙磨控制系统的设计与实现[J].自动化仪表,2009,30(2):27 -29.
[5]席爱民.模糊控制技术[M].西安:西安电子科技出版社,2008.
[6]王祥好.模糊PID控制算法在智能小车中的研究与应用[D].合肥:合肥工业大学,2009.
[7]南新元,陈志军,程志江.基于模糊PID控制的电锅炉温度过程控制系统[J].自动化仪表,2008,29(5):5 -8.
[8]尹晓落.模糊PID控制在直流调速系统中的应用[D].合肥:合肥工业大学,2008.
[9]徐大诚,邹丽新,丁建强.微型计算机控制技术及应用[M].北京:高等教育出版社,2003.
[10]赖寿宏.微型计算机控制技术[M].北京:机械工业出版社,2010.
