目标位置误差对威胁等级评定影响的分析模型

周国辉，谢 井，李 鼎

（海军指挥学院信息战研究系，江苏 南京 211800）

0 引言

一般可以将防空作战过程抽象为目标侦察探测、目标威胁判断、作战指挥控制三个阶段［1－2］，目标威胁判断即评定目标的威胁等级，对指挥决策至关重要。目前已对目标威胁判断进行了大量的研究，研究方法主有多属性决策、层次分析法、D－S证据理论、模糊神经网络、灰色理论等［3－6］，且多是研究威胁等级的评定。然而在防空作战中，威胁程度不高的目标可能被误判为严重威胁目标而导致资源的浪费，威胁程度很高的目标被误判为轻微威胁目标而延误了对抗的最佳时机并最终导致防空作战的失败，因而目标威胁等级的错误判断将在一定的程度上直接影响防空作战的效果。由于从威胁等级误判这一角度展开的研究未见报道，因此本文主要从威胁等级错误评定角度，研究分析防空作战中反舰导弹的目标信息误差对威胁等级评估的影响。

1 目标信息误差模型

完整、准确、及时的目标信息是决策的基础，目标位置信息的准确性将影响决策效果，必对威胁目标等级评定产生影响［7］。以编队的方式对反舰导弹进行预警探测，必须对各个侦获的目标进行信息融合。因而由目标信息产生的过程［8－9］可以获知，目标位置误差除了由雷达探测产生外，坐标转化、信息融合的时间同步也将产生目标的位置误差。

1.1 探测误差模型

反舰导弹位置信息主要为目标斜距R、俯仰角β和方位角ε三种信息类型，而弹体的其他位置信息如速度、高度、距地面目标的距离均可以由（R，β，ε）来确定。对反舰导弹的探测误差主要包括测距误差ΔR、俯仰角误差Δβ、方位角误差Δε。令R、β、ε为测量值，Rm、βm、εm为目标的真实值。假设雷达对目标的距离测量结果服从R～N（Rm）的正态分布，而误差方差的平方σ有［10］

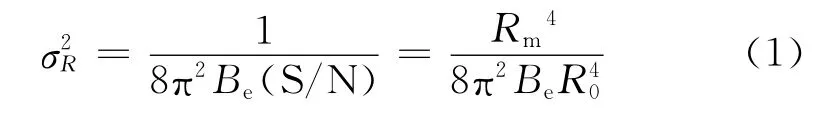
式中，Be为均方根带宽，S／N为信噪比，R0为信噪比为1时雷达作用距离。

由式（1）知，在目标距离越远时，对目标的距离测量误差方差就越大，并可简单假令σR＝kRRm2，其中kR为常系数，不同的雷达取值不同，雷达波包络信号的均方根带宽Be、波长、发射功率、发射天线增益越大，则kR取值越小。

同理，角度测量值也满足正态分布，有β～N（βm，），可令σβ＝k；ε～N（εm），可令σε＝。

1.2 坐标转换引入误差模型

将各部雷达获取的目标信息进行融合时必须对参考坐标进行统一，一般是将以指挥站（或融合站）为中心的极坐标系转换成适合的坐标系，或将其他站获取的目标位置信息变换至本站坐标系内。坐标变换将对测量误差作非线性处理［11］。进行坐标变换时，主要考虑的数据参数为斜距R、方位角β、俯仰角ε，进行信息融合时，设转化后的坐标参数分别为ξ、υ、γ。设变换前后的非线性关系为：

式中，V＝（Δξ，Δυ，Δγ）T，T＝（ΔR，Δβ，Δε）T，Q为误差变换系数矩阵。

在实际的舰艇编队防空反导的侦察探测网中，就存在极坐标与极坐标之间的变换，并且可以认为它们的坐标原点处于同一水平面上，即是将极坐标Oρ 中的点S （R，β，ε）坐标值变换到极坐标O′ρ 中，坐标变换引入误差便体现在极坐标与极坐标的变换过程中，由误差变换系数矩阵Q决定，具体可参考文献［12］。

1.3 时间同步引入误差模型

在原坐标系中取目标飞行速度为νm，融合时间对准误差为σt，则时间同步引入误差为νmσt。假设在原极坐标Oρ中，目标的速度可以表示为νm（vR，vβ，vε），则在原坐标系中经时间同步引入的误差为：

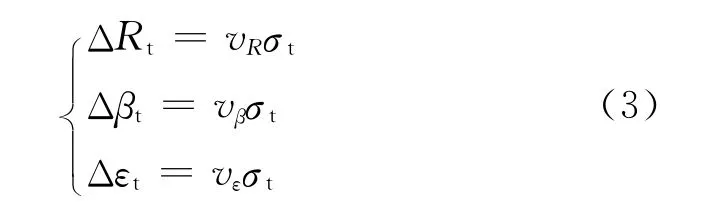
综合考虑三方面因素，在计算目标的位置信息误差经坐标转换及时间同步后，转换后的坐标系内获得的目标误差为：

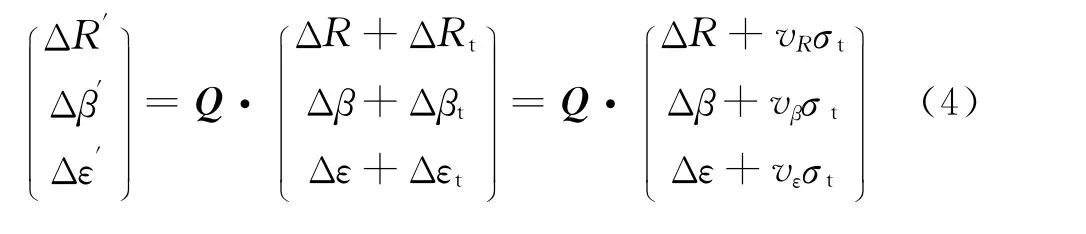
2 威胁等级错误评定概率模型

反舰导弹位置误差对威胁等级评定的影响主要体现在使得目标的测量数据远远偏离目标的真实情况，从而造成威胁评定结果的错误，这种错误程度便能反应出目标位置误差对威胁评定的影响。因而，本文建立威胁等级错误评定概率P这个目标指标，用于度量错误评定的程度大小。若P越大，出现评定结果错误的可能性就越大，则误差造成的影响就越大。

假定对反舰导弹威胁等级的评定集合为I＝｛J1，J2，J3，…，Jm｝，J1，J2，J3，…，Jm按威胁等级从高到低进行排列，J1的威胁等级为最高，Jm的威胁等级为最低。考虑更一般的情况，设进行威胁等级评估的n个因素（或称特征参数）构成N维空间，每个参数对应一维，N维空间的边界为各个参数的边界值，可以是清晰的边界，可以是模糊的边界。并且可以假定J1，J2，J3，…，Jm这m 个评定等级可以映射到N维参数指标空间的某一空间区域，即N维参数指标空间被对应地划分为m个区域空间：

且Ω1→J1，Ω2→J2，…，Ωm→Jm。

显然，任意反舰导弹均可以与N维参数指标空间中的某个具体点S （ξ1，ξ2，ξ3，…，ξn）相对应，判断的依据为：

若S（ξ1，ξ2，ξ3，…，ξn）∈Ωi，i＝1，2，3，…，m，则反舰导弹的威胁等级为Ji。

因此，威胁等级i错误评定概率Pi，可以理解为将威胁等级为Ji的反舰导弹评定为其他威胁等级的概率P，即为：

只考虑目标位置信息误差对威胁等级评定的影响，假定对应的指标为ξ1、ξ2、ξ3，则错误评定概率为：

式中，Rm、βm、εm为目标真实坐标，ΔR′、Δβ′、Δε′为目标信息误差值，由式（4）求得。

由第1章对目标位置误差的分析可以得知，当目标点S （Rm，βm，εm）在空间区域Ωi内变化时（可视为均匀分布），则雷达的探测误差也将发生变化，转换矩阵Q也不尽相同，则不同目标点的信息误差应分别计算。可采用随机模拟［13］的方法，以错误评定的统计结果来替代威胁等级的错误评定概率。

3 仿真试验

假设某舰艇编队进行防空反导作战中，有源雷达A（主站，兼编队的指挥中心）和有源雷达B（雷达哨舰）构成一个简单的防空探测网，目标为对A所在舰艇进行攻击的反舰导弹D，为降低导弹D对雷达A的搜索概率，探测网采取的策略为雷达A静默关机，雷达B负责对目标进行探测并为A提供目标信息。A座对反舰导弹等级评定简单指定如下（暂只考虑依据目标的位置信息进行评定），评定等级为5级，本例仅定量分析目标位置误差对实际威胁等级评定为1级（威胁等级最高）的影响，该级对应的参数指标空间为Ω1＝ ｛（0km，10km），（0°，5°），（30°，60°）｝。由 式 （2）可获得距离误差系数k1的大致取值，其中距离度量单位为km，俯仰误差k2、俯仰误差k3取值方法类似。

仿真设置1：雷达B与雷达A的相对位置、反舰导弹的运动参数、时间对准误差固定，设置B座的位置对应A座坐标系中的坐标为O′（5km，0°，45°）；导弹飞行速度为300m／s，俯仰转动速度为0.1（°）／s，方位角转动速度为0.2（°）／s；融合时间对准误差为2s；仿真循环次数N＝10 000，其仿真结果如表1所示。

表1 仿真试验1的结果数据表Tab.1 Data result of experiment 1

仿真结论1：误差系数k1、k2、k3的取值越大，则对应的雷达探测误差就越大，而威胁等级错误评定概率就越大；若只考虑雷达自身的测量误差，则计算的错误评定概率小于综合考虑各类误差时计算的威胁等级错误评定概率，因此经过坐标转换和信息融合后，使得对反舰导弹威胁等级的错误评定概率增大。组网探测虽然作用威力上有很大优势，但由于坐标转换引入误差和信息融合时间对准误差的存在，反而使得对反舰导弹威胁等级的错误评定概率增大，该结论与实际情况吻合。

仿真设置2：雷达B与雷达A的相对位置、对反舰导弹的探测误差固定，设置探测误差系数k1为0.000 1，k2为0.001，k3为0.001；B座的位置对应A座坐标系中的坐标位置为O′（5km，0°，45°）；仿真循环次数N＝10 000，其仿真结果如表2所示。

仿真结论2：反舰导弹的运动特性和信息融合时间共同影响威胁等级的正确判断：当导弹运动较慢、融合时间对准误差较少时，对反舰导弹的威胁等级错误评定概率较小；当导弹速度运动很快、融合时间对准误差较大时，威胁等级错误评定概率较大，该结论与实际情况一致。

仿真设置3：反舰导弹的运动参数、时间对准误差以及对反舰导弹的探测误差固定，设置导弹飞行速度为300m／s，俯仰转动速度为0.05°／s，方位角转动速度为0.05°／s；融合时间对准误差为1s；探测误差系数k1为0.000 1，k2为0.001，k3为0.01，仿真试验结果如表3所示。

表2 仿真试验2的结果数据表Tab.2 Data result of experiment 2

表3 仿真试验3的结果数据表Tab.3 Data result of experiment 3

仿真结论3：在反舰导弹的运动、时间对准误差以及对反舰导弹的探测能力确定时，坐标系之间的距离对威胁等级错误评定概率影响很大，而坐标系之间的方位角影响不大，如表3中，坐标系之间的距离固定时，改变B对应A坐标系的坐标方位，但错误评定概率在一定范围波动，无明显变化趋势。该结论与以往的分析结论吻合，说明威胁等级错误评定概率模型与实际情况相一致。

4 结论

本文提出了目标信息误差对威胁等级评定影响的分析模型。该模型首先综合了雷达的探测误差、坐标转换引入误差和信息融合时间同步引入误差，求导出目标位置误差的度量模型，通过对目标位置误差对反舰导弹威胁等级评定的影响分析，提出了威胁等级错误评定概率的度量目标指标和求解方法。仿真结果表明：通过设置不同的仿真条件，能够求解舰艇编队在不同条件下对来袭导弹的威胁等级错误评定概率，同时也验证了威胁等级错误评定概率模型符实、可用。论文的不足或改进点主要体现在选取的反舰导弹威胁等级评定模型需进一步深入研究。

［1］孙宏纲，姚景顺.舰艇编队防空作战信息流程研究［J］.舰艇学术研究，2005（1）：27－28.

［2］陈康，罗雪山，罗爱民.CEC条件下的舰艇编队防空问题［J］.火力与指挥控制，2006，31（4）：32－35.CHEN Kang，LUO Xueshan，LUO Aiming.Research on surface ship formation air defense based on cooperative engagement capability［J］.Fire Control and Command Control，2006，31（4）32－35.

［3］徐奕航，童幼堂，张磊，等.基于编队的导弹目标威胁判断排序模型［J］.海军大连舰艇学院学报，2008，31（6）：22－24.XU Yihang，TONG Youtang，ZHANG Lei，et al.Queuing model of threat estimation of missile target based on warship formation［J］.Journal of Dalian Naval Academy，2008，31（6）：22－24.

［4］刘雁兵，刘付显.基于模糊神经网络的空袭目标威胁评估［J］.战术导弹技术，2005（3）：9－12.LIU Yanbing，LIU Fuxian.Air－attack targets threat evaluation method based on fuzzy neural network［J］.Tactical Missile Technology，2005（3）：9－12.

［5］骆文辉，刘少伟，杨建军.基于灰色区间关联决策的目标威胁评估［J］.空军工程大学学报，2008，9（3）：37－41.LUO Wenhui，LIU Shaowei，YANG Jianjun.Threat evaluation technology based on grey interval－number for grey decision－making［J］.Journal of Air Force Engineering U－niversity（Natural Science Edition），2008，9（3）：37－41.

［6］潘红华，王建明，朱森，等.目标威胁判断的模糊模式识别模型［J］.兵工学报，2004，25（5）：576－580.PAN Honghua，WANG Jianming，ZHU Sen，et al.A fuzzy pattern recognition model for the threat evaluation of targers［J］.Acta ArmamentarII，2004，25（5）：576－580.

［7］陈立新.防空导弹网络化体系效能评估［M］.北京：国防工业出版社，2007.

［8］BLOEMEN AF，WITBERG RR.Anti－air warfare research for naval forces［J］.Naval Forces，2000，21（5）：20.

［9］Alerts，David S，John Garstka，Frederick Stein.Network centric warfare：development an leveraging information superiority［M］.Wanshington DC：CCPP Publicaion Series，1999.

［10］丁鹭飞，耿富录.雷达原理［M］.第三版.西安：西安电子科技大学出版社，2004.

［11］董洪乐.反导系统威胁目标信息移交研究［D］.北京：国防科技大学，2006.

［12］何友，修建娟，张晶玮，等.雷达数据处理及应用［M］.北京：工业出版社，2009.

［13］刘宝碇，赵瑞清，王纲.不确定规划及应用［M］.北京：清华大学出版社，2003.