基于模型预测控制的自适应噪声抵消方法
2012-12-01竺小松李永涛
敦 鹏,竺小松,李永涛
(1.解放军电子工程学院,安徽 合肥230031;2.解放军65301部队65分队,吉林 长春 130000)
0 引言
自适应噪声抵消方法[1]的特点是在没有或很少的关于信号和噪声的先验知识条件下,利用前一时刻已获得的滤波器参数来自动调节现时刻的滤波参数,以适应信号和噪声未知或随机变化的统计特性,从而实现最优抵消。
根据文献[2]所述,经典滤波器设计应用于实际噪声相消系统中,由于传统的处理方法都是基于对噪声(或不确定性)的随机描述,即假设系统中的噪声(或不确定性)服从一定的概率模型,然后再根据不同的假设条件,采用相应的估计准则完成自适应干扰抵消算法。然而,现实实践中,由于观测误差、模型结构误差以及随机噪声等多种不确定因素的存在,使得基于噪声(或不确定性)统计特性方法的假设条件一般很难得以满足,这是因为噪声(或不确定性)的概率统计信息常常是缺乏的,甚至在很简单的情况下,其分布也是有争议的。而且,在实际应用中,自适应干扰抵消技术应该具有模型简单、实时性消噪,能有效处理约束和鲁棒性强等特点。因此本文提出了一种基于模型预测控制的自适应噪声抵消方法。
1 模型预测控制自适应系统的基本原理与自适应噪声抵消算法简介
1.1 模型预测控制自适应系统的基本原理
根据文献[3]所述,预测控制属于一种基于模型的控制算法,此种算法的基本特征是预测模型、滚动优化和反馈校正。预测控制能够很好地解决系统在不确定性因素的影响下能保持良好的鲁棒性,且算法简单,易实现。由于预测模型是利用过去和现在的已知数据信息预测系统未来的输出行为,因此用预测控制来约束自适应噪声抵消系统可以解决无先验概率的难题,并可以对噪声进行实时的跟踪对消。此外预测控制能够根据功能的需求按最方便的途径建立模型,在工业实际中得到广泛应用[4]。
预测控制自适应系统取控制对象输出在未来的采样点上跟踪某一期望轨迹的方差最小;对于本文的要求,取控制能量为最小,并且同时保持输出在某一给定范围内时,本文针对信号噪声相消特性提出性能指标如下式:
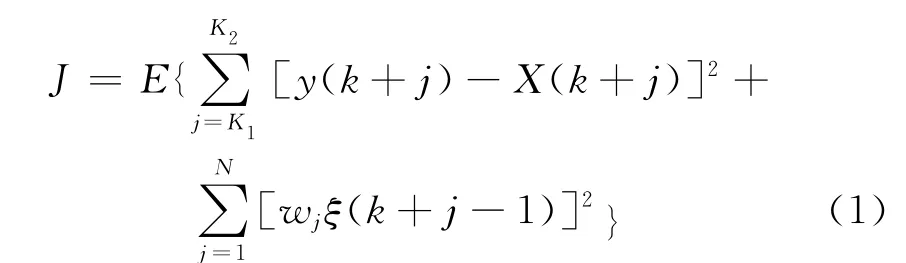
式(1)中,y(k+j)和X(k+j)为系统未来时刻k+j时的实际输出和期望有用信号输出;N为误差信号采样长度,K1为采样信号的现在采样点,K2为信号预测的截止采样点,wj为滤波器的加权系数,一般取为常数。将使未来输出预测序列y(k+j)沿某个参考轨迹yr(k+j)到达设定值。利用优化目标的滚动式的有限时域优化策略,反复对信号的系统预测输出信息进行调整。具体过程为:
第一步:在k采样时刻,优化性能指标只涉及未来k+K1到k+K2的有限的时域;
第二步:将误差信号通过对滤波器的调整,将优化性能指标达到最低。
以上两步骤在线反复进行,在每个采样点上都对固定数目的预测采样点逼近,最终将误差信号消除或降低到所要求的最小值,系统达到了稳定状态,完成了消噪的作用。可以看到,消噪的过程始终把优化过程建立在从实际过程中获得的最新信息的基础上,能更好地利用过去和当前的采样点对误差实时性的优化,对先验概率要求很少。
该自适应系统利用反馈校正,由于实际系统中存在的非线性、时变、模型失配和干扰等不确定因素,那么利用当下采样点与参考信号的差值,即为误差信号对系统进行优化,优化的过程是对系统的动态范围不断地缩小的过程。利用模型预测控制原理可知,通过这种反馈校正,确定一组未来的控制作用[ξ(k),…,ξ(k+N-1)],这种控制作用本质上为预测的系统输出误差。这些控制作用是按照实时的当前时刻采样的控制,到下一采样时刻,则首先检测对象的实际输出,并利用这一实时信息对基于模型的预测指标进行修正,然后再进行新的优化。
1.2 自适应噪声抵消算法简介
根据文献[5]所述,自适应噪声抵消系统的处理对象为干扰噪声,它的作用就是自适应抵消掉干扰噪声或者对噪声进行大幅度衰减,从而提高信号传递和接收时的信噪比(SNR)。其原理概述为,首先应用相关噪声信号通过参考通道中的自适应滤波器输入;然后在滤波器中,经由一种受误差信号控制的算法自动地调节滤波器的冲激响应,使得输出在遵照最小均方准则的基础上,最接近主通道的干扰信号;最后经求和器使两个通道的信号相减,抵消主通道中的干扰信号。若使用的优化算法得当,滤波器可在变化的条件下工作,通过不断地自动调整,使误差信号始终保持最小。图1为自适应噪声抵消原理框图。其中主信道端为混合信号S=X+N0;X为有用信号,N1为噪声的参考信号,且与N0相关,而与X不相关;自适应滤波器输出y(n);系统输出是E(n)。
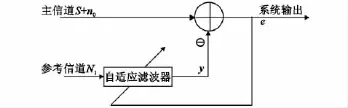
图1 自适应噪声抵消原理框图Fig.1 Diagram of adaptive noise cancellation principle
2 基于模型预测控制的自适应噪声抵消方法
本文基于模型预测控制自适应噪声抵消方法是在传统的自适应噪声抵消方法的基础上利用模型预测控制算法建立模型控制系统结构,其原理是:首先利用相关噪声信号通过自适应滤波器的输出与主信道中接收的信号形成控制误差信号E(n);然后在滤波器中,经由模型预测控制算法自动地调节滤波器的冲激响应,优化控制误差信号;最后计算输出信号y(k)与控制误差信号遵照的最优控制性能指标J。通过不断地自动调整,使得J始终保持最小,此时的输出信号即为纯净信号。
如图2所示,即为基于模型预测控制自适应噪声抵消的原理框图。该系统结构改变了传统的自适应噪声抵消系统直接利用滤波器输出误差对其权值的优化结构,是将当前输出的误差控制通过模型预测控制模块,利用模型预测控制算法对误差控制优化,目的是使得整个自适应噪声抵消系统在误差控制及其预测参数的控制下消除噪声。

图2 基于模型预测控制自适应噪声抵消的原理框图Fig.2 Based on MPC of adaptive noise cancellation principle
对接收的混合信号S采样,在每个“当前采样时刻k”,基于系统性能指标的预测模型,利用过去、当前和将来的误差控制输入以及过去和当前的系统输出,对系统未来某段时间内的输出序列进行多步预测,如图2中的[y(k+1),…,y(k+N)]T。那么得到误差矩阵E(k)与输出信号y(k)和噪声参考信号N1的关系如式(2)所示:

3 理论推导与仿真验证
3.1 理论推导
将式(2)比对模型预测控制算法,其中A(z-1)和B(z-1)都是后移算子z-1的多项式。
选用的控制向量即为噪声自适应消除系统的误差信号E(k)= [ξ(k),…,ξ(k+N-1)]T。噪声参考信号为:N1= [n(k+1),…,n(k+N)]T。
未来的控制序列[ξ(k),…,ξ(k+N-1)]是通过式(1)的性能指标目标函数得到的。
引入丢番图方程[6]:
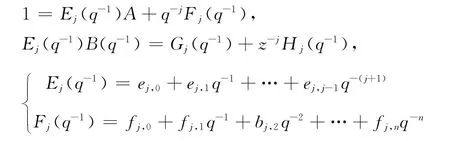
将式(2)两边乘以Ejqj得

注意到Ej、Fj的形式,可以知道z-dGjξ(k+j)与n(k+j),n(k+j-1),… 有关,Fjy(k)只与y(k),y(k-1),… 有关,而Ejn(k+j)与n(k+j),…,n(k+1)有关。由于在k时刻未来的噪声参考值ξ(k+i),i=1,…,j都是未知的,所以y(k+j)最适合的误差预测控制值可由下式得到:
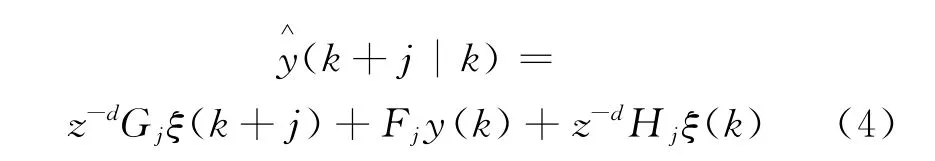
从上面的式子可知,基于模型预测控制的自适应噪声相消技术对噪声的先验概率几乎不作要求。
将式子写成向量形式,则系统将来时刻的最小方差输出预测模型:
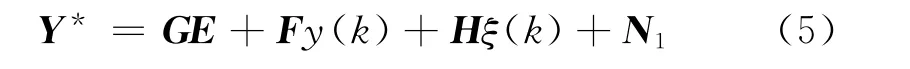
式中,Y*=(k+d|k),(k+d+1|k),…,

将控制信号(自适应系统中的误差信号)E极小化目标函数
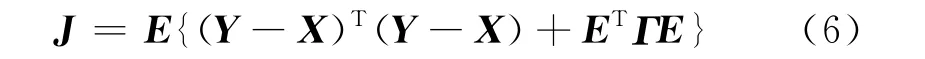
将式代入,并求∂J/∂ξ=0得最优控制律:

尽管预测控制在每一控制周期内,通过优化某个性能指标,可获得N个未来控制作用{ξ(k+j),j=0,1,…,N-1},但在当前时刻k,仅对过程实施当前时刻的控制作用ξ(k)。
完成一步采样后,将所有序列平移,准备进行下次采样。在下次采样后,上述过程都需要重复进行,以便根据最新实测数据更新未来控制序列,即实现反馈校正和滚动优化。可以看出基于模型控制的自适应噪声抵消方法只是利用系统已有误差控制和预测的误差控制对自适应滤波器的权值进行优化控制,对先验概率要求并不严格。
3.2 仿真
依照自适应噪声抵消系统原理,结合模型预测控制二者特点,构成了基于模型预测控制自适应噪声抵消系统。为了简化说明问题,根据系统结构图2,模型预测控制自适应抵消系统利用Matlab仿真时,设定输入为正弦信号,由模型预测控制和加法器组合构成自适应噪声抵消系统,输入信号经由自适应噪声抵消系统作用后产生输出。仿真结果如图3和图4所示。图3所示为接收的混合信号S和干扰信号N0,图4所示为控制信号和系统输出信号y(n)与有用信号x(n)的对比。

图3 原始信号Fig.2 The original signal

图4 系统仿真结果Fig.4 Simulation results
仿真实验说明:经模型预测控制处理后的自适应消噪系统,收敛速度,具有良好的鲁棒性,主通道信号经过求和器与预测模型输出抵消后,得到基于最小均方准则下对输入信号的最佳消噪效果。
综上所述,基于模型预测控制的自适应噪声抵消系统达到了实际应用的效果,有效地消除了噪声使信号保持了原来的特性,因此,对模型预测控制自适应噪声抵消的研究是非常有意义的。
4 结论
本文提出了基于模型预测控制的自适应噪声抵消方法,将自适应噪声抵消系统构造成了模型预测控制结构,利用误差控制及其预测对整个消噪系统控制,使得非线性自适应噪声抵消系统能实时有效地减除噪声。理论推导和仿真说明了该方法是可行的,同时可以看出该方法拥有对先验概率的依赖性小和良好的鲁棒特性等特点,因此在实际应用中,基于模型预测控制自适应噪声抵消方法更具有优势。
此外可在此系统基础上优化算法,如文献[7]利用抑制超调快速预测改进算法,可避免矩阵运算,提高跟踪速度,使该系统的噪声消除性能达到更好水平。
[1]王海涛.自适应噪声对消在引信数字信号处理系统中的应用[J].制导与引信,2009,3(30):13-17.WANG Haitao.Application of adaptive noise cancellation in fuze digital signal processing system[J].Guidance &Fuze,2009,3(30):13-17.
[2]李富强,党建亮.基于LMS算法的自适应消噪系统研究[J].河南科技学院学报,2010,9(38):100-103.LI Fuqiang,DANG Jianliang.Study on adative noise cancellation system based on LMS algorithm[J].Journal of Henan Institute of Science and Technology,2010,9(38):100-103.
[3]庞中华,崔红.系统辨识与自适应控制Matlab仿真[M].北京:北京航空航天大学出版社,2009.
[4]张少罡.预测控制方法的研究与应用[D].北京:北京化工大学,2009.
[5]王千,裴承鸣,秦淋,等.回声抵消的相关函数RLS算法[J].计算机仿真,2010,27(7):350-353.WANG Qian,PEI Chengming,QIN Lin,et al.RLS algorithm based on correlation function for echo canceling[J].Computer simulation,2010,27(7):350-353.
[6]王伟,杨建军.广义预测控制:理论、算法与应用[J].控制理论与应用,1997(12):777-786.WANG Wei,YANG Jianjun.Generalized redictive contol:theory,algorithm and alication[J].Control Theory and Alications,1997(12):777-786.
[7]吴夏来.广义预测控制简化算法研究[D].浙江:浙江理工大学,2010.
