支持更新的XML编码方案

杨 扬，申石磊

（河南大学 计算中心，河南 开封475004）

0 引 言

XML作为互联网上一种功能强大的标记语言，已经成为数据表示和交换的一个主要标准，受到越来越多的业内人士的关注，如何高效的索引和查询XML数据是目前XML研究领域的重要课题。为了加速结构连接，提高查询和文档更新维护的效率，目前主流方法是通过对XML文档树编码，依靠编码快速判断结点间的结构关系。研究人员提出了很多编码方案来加速结构连接，但是大多没有考虑编码更新问题。当XML文档更新时，更多的编码方法不能很好地支持更新操作。当XML数据频繁地发生删除、插入等更新XML数据时，需要调整相应结点的编码，以维持结点间的结构关系。但重新建立索引或重新编码的代价是非常高的，有时甚至需要给整棵树重新编码。若采用预留空间的编码方案，在一定程度上解决了动态更新问题，但当插入结点过多，超出预留空间时，仍然需要重新遍历XML文档树，造成二次编码。因此，本文提出了一种新的支持XML数据更新的编码方案IPEU （improved prefix encoding of supporting updates），该编码方案可快速判断结点间的结构关系，当XML文档树中插入或删除结点时，已有结点不存在二次编码问题，降低了更新代价，查询性能得以提高。

1 相关研究

1.1 区间编码

区间编码是树T中的每一个结点被赋予一个编码区间［start，end］，并且满足：一个结点的区间编码包含它的后裔结点的区间编码［1］。区间编码能有效地支持XML查询，但它不能适应XML文档动态更新，当在XML文档中插入和删除结点时，有时甚至会导致整个文档树的重新编码。ZHANG编码将对结点先序遍历时两次访问生成的序号作为编码，这种采用全局标识的编码更新缺乏灵活性，一个或多个结点的插入或删除操作，会引起多个甚至所有结点的二次编码。为保证能够XML文档更新，Li－Moon编码的order序号采用非连续的取值，预留了一定的空间，Li－Moon编码与Dietz编码相比，能够更好地支持文档的修改，但当插入的结点过多超出了预留空间时，就需要重新编码。

1.2 路径编码

路径编码保存了元素的路径信息，每个结点编码都继承其父结点的编码，作为其编码的前缀。文献 ［2］提出了一种适用于顺序XML文档树的前缀编码方案。这种编码方案支持顺序XML文档的XPath查询，并且编码具有动态性，可以适应XML文档的插入、删除操作，但是编码过长却是需要改进的。采用二进制表示的SP编码，编码长度过长，且在执行插入或删除操作后有大量的结点需要二次编码。同样采用二进制标记的ORDPATH编码机制类似于Dewey编码，引入了局部标识，支持XML文档更新，不需要对结点重新编码，但是预留的空间，造成了浪费，使得编码规模很大。

因此，基于以上问题的考虑，本文提出一种支持XML数据更新的IPEU编码方案，并且该编码是对文献 ［3］中IPE编码的改进，弥补了不支持编码更新的不足。IPEU编码支持XPath查询轴的计算，可表示祖先／后裔、双亲／孩子、之前、之后等关系，当执行插入或删除操作时，XML文档树中已有结点的编码不需改变，实现了结点编码动态更新，从而提高了更新和查询效率。

2 IPEU编码方案

定义1 IPEU编码：本质上是一种扩展的Dewey编码，由字母、整数、点 （.）组成，XML文档树的层次用L表示，令c（u）为结点u的IPEU编码，对于结点u的孩子结点v的IPEU编码c（v）＝c（u）Nv，其中Nv代表了结点v在结点u的所有孩子结点中的从左到右的位置关系。原Dewey编码中各层的 “.”分隔符取消，表示各层的分隔仅用数字标识。若Nv小于10，Nv仍以数字表示；若Nv大于10，除个位数字不变，其余位均做转换，其中，1转换为A，2转换为B，依次转换，直至9转为I。

图1为IPEU编码片断。

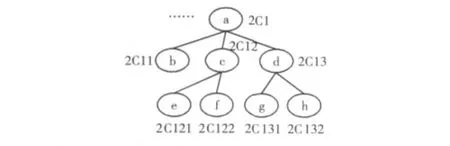
图1 IPEU编码片段

定义2 IPEU编码比较：设结点u的IPEU编码c（u），结点u的祖先结点a的IPEU编码c（a），结点u的双亲结点p的IPEU编码c（p），结点u的孩子结点c的IPEU编码c（c），结点u的后裔结点d的IPEU编码c（d），结点u的前驱兄弟结点ps的IPEU编码c（ps），结点u的后继兄弟结点fs的IPEU编码c（fs），则c（a）＜c（u），c （p）＜c （u）＜c （c），c （ps）＜c （u）＜c （fs），c （ps）＜c （d）＜c（fs）。

依据定义2中的编码符号，表1给出了基于IPEU编码，在进行XPath查询时，XML结点间结构关系的判定方法。

表1 基于IPEU编码的XPath查询

3 IPEU编码的更新

IPEU编码支持4种插入操作：①在两个相邻位置的兄弟结点之间插入新结点；②在结点的最左孩子结点之前插入新结点；③在结点的最右孩子结点之后插入新结点；④为叶子结点的孩子插入新结点。如图2所示，图中实线表示已有结点，虚线表示插入情况。插入多个结点的操作，可分解为以上4种插入操作通过多次插入来完成。以下4种插入操作IPEU编码规则如下：

（1）在两个相邻位置的兄弟结点u和v之间插入新结点t，Nu与Nv是两个相邻的整数，结点t在两兄弟结点u和v之间的位置关系Nt前加符号 “.”加以标识，结点t的IPEU编码c（t）＝c（u）.Nt，Nt取值从整数1开始。若结点t与v之间再插入新结点m，则结点m的IPEU编码c（m）＝c（t）.Nm，Nm－Nt＝1，即Nt与Nm以1为步长递增。

例如：图2（a）中两个位置连续的兄弟结点b1与b2之间插入结点b3，c（b1）＝2C11，c（b2）＝2C12，那么c（b3）＝2C11.1。b3与b2之间再插入结点b4，c（b4）＝2C11.2。

特例，若结点u与插入的结点t之间，再插入结点p，在反映结点p在u和t之间的位置关系Np前加符号 “.”标识，结点p的IPEU编码c（p）＝c（u）.Np，Np取值从0开始。若结点u与p之间再插入新结点q，则结点q的IPEU编码c（q）＝c （t）.Nq，Nq－Np＝－1，Nq与 Np以－1为步长递减。

例如：如图2（a）所示，两个位置连续的兄弟结点b1与b2之间已插入结点b3，若在b1与b3之间再插入结点b5，c（b1）＝2C11，c （b2）＝2C12，c （b3）＝2C11.1，那么c（b5）＝2C11.0。b1与b5之间再插入结点b6，c（b6）＝2C11.－1。

（2）在结点u的最左孩子结点v之前插入新结点p，结点u的IPEU编码c（u），结点v的IPEU编码c（v）＝c（u）Nv，结点v是结点u的最左孩子，Nv＝1，新结点p插入已有结点v之前，p即为u最左孩子结点，c（p）＝c（u）Np，Np＝Nv－1＝0，Np取值以－1为公差递减。

例如：在图2（b）中，在结点a的最左孩子结点b1之前插入结点b7，c（a）＝2C1，c（b1）＝2C11，Nb1＝1，c（b7）＝2C10，Nb7＝1－1＝0。若在已成为最左结点的b7之前再插入新结点b8，则c（b8）＝2C1－1，Nb8＝0－1＝－1。

（3）在结点u的最右孩子w结点之后插入新结点q，结点u的IPEU编码c（u），结点w的IPEU编码c（w）＝c（u）Nw，结点w是结点u的最右孩子，新结点q插入u之后，q变成u最右孩子结点，c（q）＝c（u）Nq，Nq＝Nw＋1，Nq取值以1为公差递增。

例如：在结点a的最右孩子结点b2之后插入结点b9，c（a）＝2C1，c（b2）＝2C12，Nb2＝2，c（b9）＝2C13，Nb7＝2＋1＝3。结点b9之后若再插入新结点b10，则c（b10）＝2C14，Nb10＝3＋1＝4。如图2 （b）所示。

（4）作为叶子结点u的孩子插入新结点v，结点u的IPEU编码c（u），结点v的IPEU编码为其双亲结点u的编码连接上结点v在其双亲结点孩子中的位次Nv，Nv取值从1开始以1为公差递增，则c（v）＝c（u）Nv。

例如：图2（c）中已插入存在的结点b8，c（b8）＝2C11－1，为b8添加孩子结点c1，c （c1）＝2C11－11。为已插入存在的结点b3先后添加孩子结点c2和c3，c（b3）＝2C11.1，则c （c2）＝2C11.11，c （c3）＝2C11.12。

其他更新操作，如删除和修改，无需改动已有的IPEU编码，这里不再赘述。

4 实 验

4.1 实验环境

本文实验环境为：英特尔酷睿2双核T5870＠2.00GHz笔记本处理器，2GB内存，160GB硬盘，Windows XP专业版（32 位／SP2／DirectX 9.0c）操作系统，NetBeans IDE 6.8for Java。

图2 IPEU编码的更新操作

实验所用数据集为XMark，其中原始XMark数据集为115MB，包含1 666 315元素，最大扇出为25 500，平均扇出为3242，最大深度12，平均深度6。实验中采用不同的生成因子生成不同大小的XMark数据集，对IPEU编码的编码时间、插入结点进行性能分析。

4.2 实验分析

（1）初始编码所用时间：采用生成因子为0.01、0.1、0.2、0.3、0.4 和 0.5 分 别 生 成 1.12MB、11.3MB，22.8MB、34MB、45.3MB和56.2MB这5个测试数据集。实验中将IPEU编码与目前普遍使用的Dewey前缀编码和Zhang区间编码作比较，这3种编码方案在对文档进行编码时的代价相差不大，如图3所示。

图3 不同编码方案所用编码时间比较

（2）编码更新所用时间：以生成因子为0.5生成的56.2MB的XMark数据集为例， （单位：千结点，1、3、5、8、10）进行了插入结点测试。Dewey前缀编码和Zhang编码不能很好地支持编码更新。当XML文档树中插入结点时，作为更新代价，为保持编码的连续性，Dewey编码将插入点之后的结点重新编码。而Zhang编码采用全局标识作为编码，这种编码查询效率较高，但XML文档更新时效率低，一旦插入或删除新的结点，整个XML文档树的所有结点均需要二次编码。而当插入新结点时，IPEU编码不需要重新编码，IPEU编码在更新数据操作时明显优于Zhang编码和Dewey前缀编码。测试结果如图4所示。实验证明，IPEU编码方案在对需要频繁进行更新的XML文档是非常有效的。

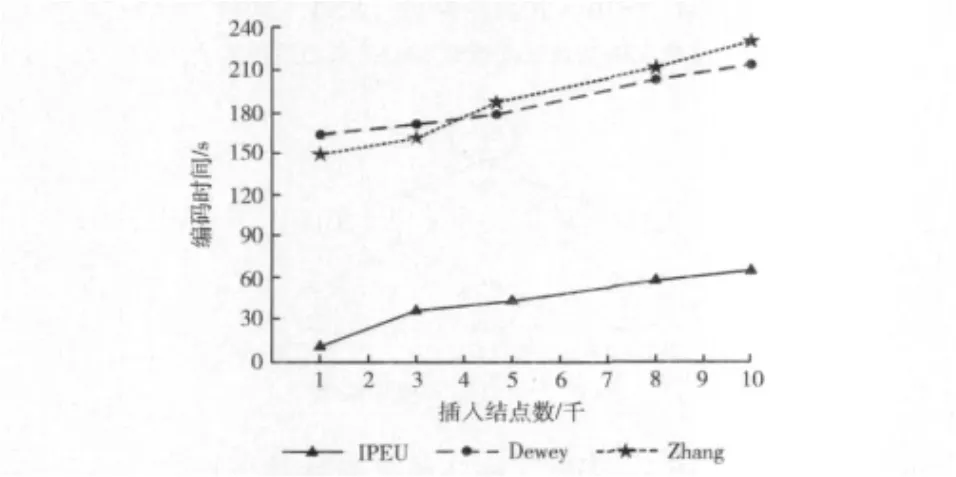
图4 不同编码方案更新操作所用时间比较

5 结束语

XML文档使用过程中，不可避免地会有修改，当增减数据元素时，若每次都得调整插入或删除结点后的结点编码，以维系在进行XPath查询时结点间的结构关系判定，这样势必会影响查询效率。为避免XML文档树中结点的二次编码，减少更新代价，本文提出了一种支持XML数据更新的IPEU编码方案，它支持祖先／后裔和兄弟等多种结构关系的判定，且编码不需要预留编码空间，这样就不必考虑当插入结点或子树时，编码预留空间不足时 “溢出”问题以及二次编码效率，不必改变已有编码，可以有效地解决更新操作所造成的结点重新编码的问题，是一种较好的前缀编码。

［1］WAN Changxun，LIU Xiping.The XML database technology［M］.2nd ed.Beijing：Tsinghua University Press，2008：106（in Chinese）.［万常选，刘喜平.XML数据库技术 ［M］.2版.北京：清华大学出版社，2008：106.］

［2］ZHANG Jianmei，TAO Shiqun.Prefix encoding scheme for ordered XML trees ［J］.Computer Applications，2005，25（12）：2879－2881 （in Chinese）. ［张剑妹，陶世群.一种适用于顺序XML树的前缀编码方法 ［J］.计算机应用，2005，25（12）：2879－2881.］

［3］YANG Yang，YIN Ke.A path query based on XML prefix encoding ［J］.Journal of Henan University （Natural Science），2010，40 （1）：85－89 （in Chinese）. ［杨扬，尹柯.一种基于XML前缀编码的路径查询 ［J］.河南大学学报 （自然科学版），2010，40 （1）：85－89.］

［4］LI C Q，LING T W，HU M.Efficient processing of updates in dynamic XML data［C］.Proceedings of the 22nd International Conference on Data Engineering.Washington，DC：IEEE Computer Society，2006：13－22.

［5］Harder T，Haustein M P，Mathis C，et al.Node labeling schemes for dynamic XML documents reconsidered［J］.Data and Knowledge Engineering，2007，60 （1）：126－149.

［6］LIU Zhenhua，Muralidhar Krishnaprasad.Effective and efficient update of XML in RDBMS ［C］.SIGMOD Conference，2007：925－936.

［7］LIU Xianfeng，ZHU Qinghua，CHEN Fengying.Research coding scheme of supporting for updating XML data ［J］.Computer Engineering and Applications，2008，44 （33）：151－154 （in Chinese）.［刘先锋，朱清华，陈凤英.支持数据更新的XML编码方案研究 ［J］.计算机工程与应用，2008，44 （33）：151－154.］

［8］MIN Junki，LEE Jihyun，CHUNG Chinwan.An efficient XML encoding and labeling method for query processing and updating on dynamic XML data［J］.Journal of Systems and Software，2009，82 （3）：503－515.

［9］KO Hye Kyeong，LEE Sang Keun.A binary string approach for updates in dynamic ordered XML data［J］.IEEE Transactions on Knowledge and Data Engineering，2008，99 （1）：602－607.

［10］WANG Chenying，YUAN Xiaojie，WANG Xin，et al.An efficient numbering scheme for dynamic XML trees ［C］.Wuhan：Proc of International Conference on Computer Science and Software Engineering，2008：704－707.

［11］LI C Q，LING T W，HU M.Efficient updates in dynamic XML data：From binary string to quaternary string ［J］.The VLDB Journal，2008，17 （3）：573－601.

［12］Fegaras，Leonidas.Efficient processing of XML update streams ［C］.Cancun，Mexico：24th IEEE International Conference on Data Engineering，2008：616－625.

［13］QIN Zunyue，TANG Yong，XU Hongzhi.Updating computing for XML document based on extended Dewey coding ［J］.Computer Engineering and Design，2009，30 （10）：2583－2589 （in Chinese）.［覃遵跃，汤庸，徐洪智.基于扩展Dewey编码的XML文档更新计算 ［J］.计算机工程与设计，2009，30 （10）：2583－2589.］

［14］XU Juan，LI Zhanhuai，LOU Ying.Novel position－based prefix encoding approach to reduce update cost for dynamic XML data［J］.Computer Science，2009，36 （2）：167－171 （in Chinese）.［徐娟，李战怀，娄颖.基于节点位置信息的降低更新代价前缀编码方案研究 ［J］.计算机科学，2009，36 （2）：167－171.］

［15］XU Liang，LING T W，WU Huayu，et al.DDE：From Dewey to a fully dynamic XML labeling scheme ［C］.Proceedings of the ACM Conference on SIGMOD，2009：719－730.

［16］WEN Si，WEN Guihua.Left child and right sibling structural join algorithm based on extended prefix－coding ［J］.Computer Engineering and Design，2010，31 （10）：2312－2319 （in Chinese）.［文思，文贵华.基于扩展前缀编码的左孩子右兄弟结构连接算法 ［J］.计算机工程与设计，2010，31 （10）：2312－2319.］

［17］ZHOU Junfeng，WEI Rui，GUO Jingfeng.Update－oriented extending Dewey labeling scheme［J］.Journal of Frontiers of Computer Science ＆ Technology，2010，4 （10）：918－926 （in Chinese）.［周军锋，魏蕊，郭景峰.面向更新的扩展Dewey编码 ［J］.计算机科学与探索，2010，4 （10）：918－926.］