路堤稳定性的探讨与研究

李丹峰

(铁道第三勘察设计院集团有限公司，天津 300142)

地基是路堤的根基，地基不稳定将危及铁路运营的安全，因此应当充分认识地基稳定的重要性，在设计中，一般采用稳定系数对路堤地基的稳定性进行评价。

1 路堤地基的破坏形式

路堤地基的破坏一般分为以下几种。

冲切剪切破坏:当路堤地基为软土或者松散的砂类土时，在列车及路堤填土荷载作用下，地基将产生大量沉降，路堤竖向切入土中，发生冲剪破坏。

局部剪切破坏:当路基换填深较大或采用反压护道加固时，由于反压护道或上部填土产生的旁侧荷载大，从而阻止路堤发生整体滑动破坏，使地基发生底部局部剪切破坏。

地基整体破坏:地基上部承受荷载较大时，地基中的塑性变形区扩展连成整体，导致地基发生整体滑动破坏。若地基中有较弱的夹层，滑动面则沿着弱夹层滑动;若地基土较为均匀，则滑动面为一曲面。在理论计算及工程设计中，一般假设滑动面线近似为折线、圆弧或两端为直线中间为曲线。本文则依据潜在滑移面理论确定了地基破坏面的形状。

目前铁路路基设计中都是在整体剪切破坏的条件下，通过对地基破坏面形状和位置进行假设分析计算得到的，本文所提出的基于潜在滑移线理论确定的地基最危险滑面位置及稳定系数也是在整体剪切破坏的条件下得到的。

2 路堤地基稳定性分析方法

按照土的强度理论确定地基稳定性的方法基本可分为两种类型:第一种是采用土体的极限平衡分析方法;第二种是采用数值方法按地基塑性区(剪切破坏区)发展的范围界限确定。

2.1 极限平衡法

极限平衡法［1］需先设定一个假定的地基土体破坏面，根据破坏面土体的极限平衡条件写出平衡方程，然后求得地基的稳定系数。该法是传统的用来求土体稳定性的方法。

奕茂田等［2］在文献中将传统的极限平衡法加以改进，对地基稳定性问题建立了理论上严谨，应用性广泛的统一分析方法，该方法的突出特点是无需事先假定地基土体的破坏机构。奕茂田等［3］又将土体稳定分析的滑动楔体模型加以改进，建立了能合理考虑土体破坏机制的更一般的滑动楔体分析技术。将该分析技术应用于地基稳定性的计算表明，这种方法具有较好的实用性和相当的精度。

2.2 数值方法

在外荷作用下，地基土体出现塑性变形区后，仍然采用弹性理论计算，这在理论上就不严密［1］。土体的力学特性非常复杂，到目前为止，关于土的本构模型理论仍处在不断发展，并且还没有哪个数学模型能精确的表述土的全部复杂特性［4］。所以，想得到一个精确的地基土体的应力场、地基沉降变形几乎是不可能的。

目前地基计算模型大致可分为弹性地基模型和非线性地基模型两大类［5］。弹性地基模型主要有Winkler地基模型、弹性半无限地基模型、双参数地基模型和分层地基模型。非线性地基模型常见的有Duncan-Chang非线性模型、非线性K-G模型、理想弹塑性模型、剑桥模型、Lade-Duncan弹塑性模型等。

3 潜在滑移线理论在路堤稳定分析中应用的研究

3.1 研究现状

张国祥［6］提出潜在滑移线(面)理论，并将其应用在边坡稳定性分析中。李丹峰［7］［8］以该理论为基础，通过对浅基础下地基土体采用有限元分析，得到地基的应力场，并编写后处理程序，对分析结果进行后处理，计算得出了浅基础下地基土体的一系列潜在滑移线。

含镓石榴石混晶是将石榴石晶体中的一种或多种元素被其他元素取代而得到的晶体，可以看做是多种石榴石晶体的固溶体．目前，研究较多的含镓石榴石混晶主要包括Gd3(Ga1-xAlx)5O12 (GGAG)，Gd3Sc2Ga3O12(GSGG)，Gd3-xLaxGa5O12(LaGGG)，Gd3-xLuxGa5O12 (LuGGG)，Lu3ScxGa5-xO12(LuSGG)，GdxY3-xSc2Ga3O12(GYSGG)等．

在铁路设计中，一般采用极限平衡法计算路堤的最危险滑面位置及稳定系数。该法优点在于采用刚塑性理论的极限平衡稳定性分析，能避开追踪实际加载应力路径的逐步增量非线性计算，直接推求出土体的稳定系数，线性计算速度快，且有成熟的软件供设计者使用。缺点是简化了土的应力应变关系，在理论上不太严密。

本文将潜在滑移线理论应用在路堤稳定性分析中，结合有限元分析，则可考虑土的应力应变关系非线性、复杂的边界条件以及实际的荷载经历，计算出路堤的稳定系数及最危险滑面位置。

3.2 数值求解步骤

(1)地基计算区域内的应力场

通过有限元分析软件模拟路堤的各种边界条件，所处场地的地质条件以及实际的荷载经历，建模、加载、求解后，可以得到任一单元、节点信息(坐标、材料特性、应力、应变等)。给定任一点P(x1，y1)，则可根据单元信息首先确定该点所属单元以及该单元各节点的信息、材料特性，然后依据单元形函数插值求得该点的应力状态(σx，σy，τxy)。

(2)地基计算区域内任意点应力信息

已知场区内任意一点P(x1，y1)，则该点主应力σ1、σ3大小、方向可以按下式确定

两个主应力 σ1、σ3与 x轴的夹角 θ1、θ3为

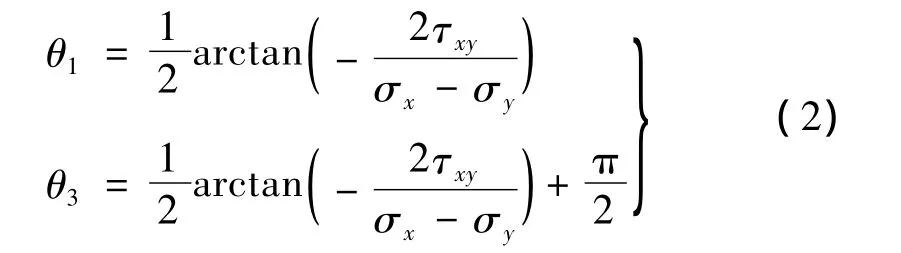
(3)地计算区域内任意点滑移线方向

通过滑移线方程［6-8］，可以求得任意点的滑移线方向与x轴夹角，以及该点的安全系数。滑移线方程的解析解几乎不太可能，本文采用Runge-Kutta方法求得滑移线方程的数值解。

(4)地基计算区域内任意点的安全系数

由文献［7］［8］［9］，任意点的安全系数FS可表示为

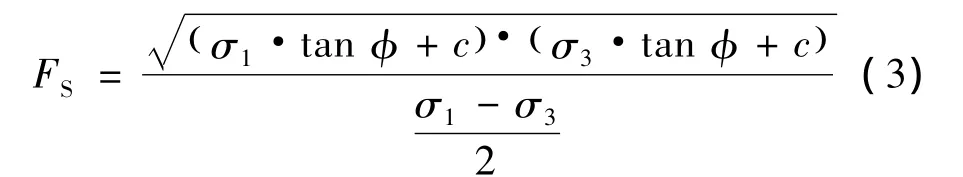
(5)地基计算区域内滑移线下一点及弧长增量

设潜在滑移线弧长增量为d s，最危险滑面切线与大主应力作用线夹角为μ，而该点滑移线的方向为(θ1±μ)，则 d x为

根据上式，应用Runge-Kutta法对滑移线方程进行数值求解，得到d y，从而生成滑移线的下一点P'(x，y)

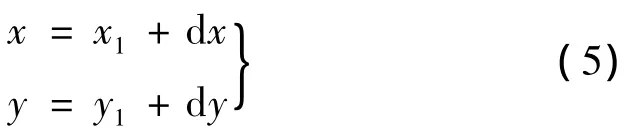
(6)局部坐标求解

有限元分析得到的是地基计算区域内，划分网格后各个节点的应力状态，若想求得地基中任意点P'(x，y)的应力状态，必须通过其所在单元的形函数进行插值。因此，必须求得该点所在单元的局部坐标P'(r，s)，才能通过该点所在单元的形函数进行插值求得该点的应力状态，从而求得主应力方向，滑移线方向等。在局部坐标系里面

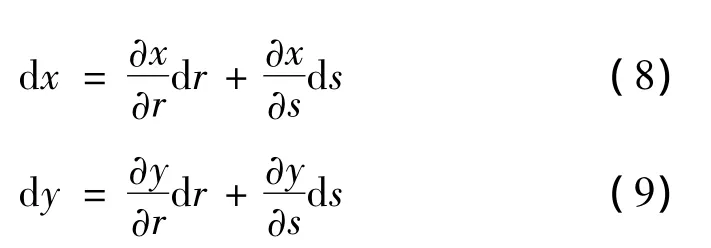
联立式(8)和式(9)可求得

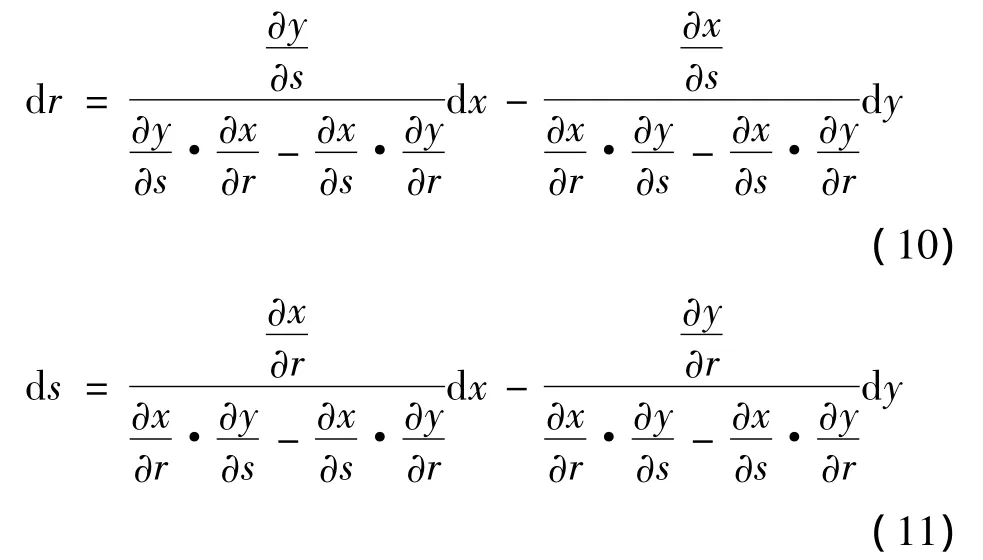
当已知点P(x1，y1)的局部坐标P(r1，s1)，则可通过下式求得P'(r，s)

(7)安全系数

当滑移线超出地基计算区域，则说明该条滑移线计算完毕，通过下式可求得整条滑移线的安全系数FS

3.3 程序流程

根据上述理论编制了求解地基潜在滑移线和安全系数的C++语言程序，其程序框架如图1所示。

4 算例

某铁路路堤填高4.0m，路基面宽7.8m，路堤边坡坡率1：1.5，地基为黏土，天然重度 γ=18.2 kN/m3，内摩擦角 φ =18°，黏聚力 c=9 kPa，泊松比 ν=0.3，地基的弹性模量E=13.8 MPa。

4.1 计算模型

首先对该路堤地基计算模型进行有限元建模分析，地基计算模型如图2，有限元分析时采用Drucker-Prager模型，把土的自重作为地基的初始应力场加到有限元模型上。首先，不考虑路堤填土及列车荷载的影响，单独对地基土体进行有限元分析，得到地基土体的初始应力场;然后，将上述地基的初始应力场加到地基单元的各节点上，模拟地基土体实际的荷载历程(填土、列车荷载等)，重新进行有限元分析计算。

4.2 数值计算分析

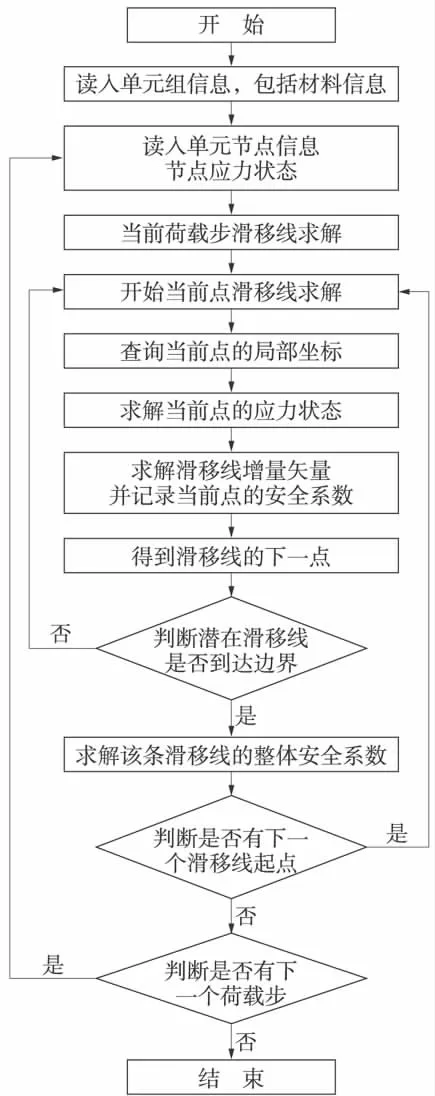
图1 程序流程

图2 地基计算模型

通过有限元分析，输出地基计算区域内的单元组信息，包括材料信息，以及地基的应力场。然而要想实现绘制潜在滑移线并求解安全系数，将是一个复杂的数值计算过程。C++语言具有很好的数据封装性，对于编写此程序提供了方便。作者通过自编的基于潜在滑移线理论的后处理程序，对这些结果进行后处理，可以画出地基对应的一系列潜在滑移线(如图3)，该地基模型的几何形状以及受力情况呈对称性，因此两组滑移线及其安全系数也是对称的。本文选取右侧一组滑移线进行分析研究。

图3 地基的潜在滑移线

图3中各条潜在滑移线对应的安全系数如表1所示，第九条滑移线的安全系数最小为1.452，所以最危险滑动面为第九条滑移线。

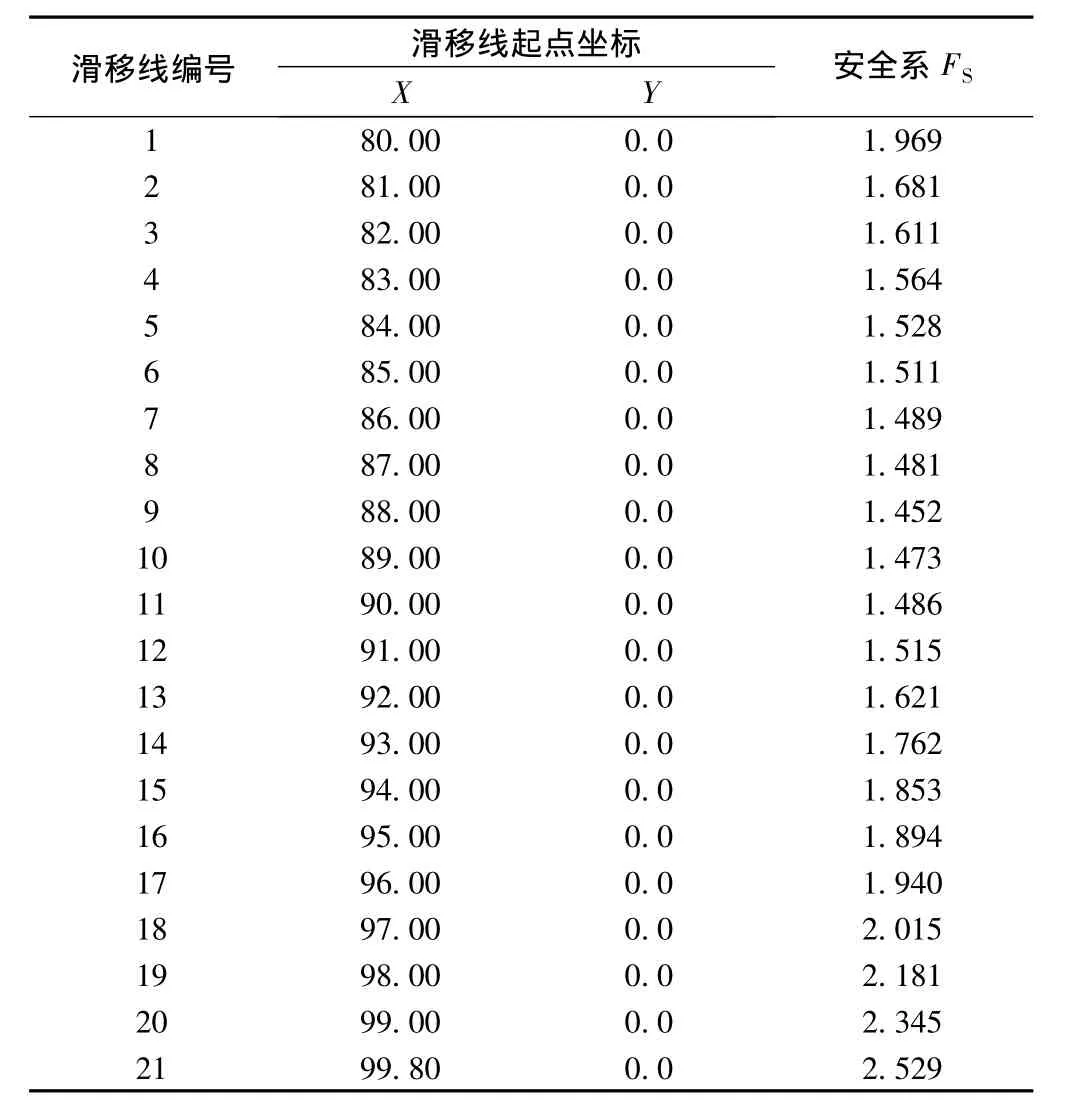
表1 各条滑移线的安全系数

5 结论

(1)该法计算绘制出的路堤地基土潜在滑移线形状与地基破坏时的滑动面形状相似，证明了该方法的可行性。

(2)利用有限元分析可以揭示出路堤在填土和列车荷载作用下，地基土体可能受损或破坏的部位，但是却不能利用有限元分析结果得出合适的定量衡量稳定性程度的指标和建立一套评价稳定性的标准，本文通过潜在滑移线理论，编写了一套有限元后处理程序，解决了该方面的问题。

［1］Chen W F.Limit analysis and soil plasticity.Elsevier scientific publ.New York:Comp，1975

［2］栾茂田，金崇磐，林皋.土体稳定分析极限平衡法改进及其应用［J］.岩土工程学报，1992，14(增刊):20-29

［3］栾茂田，金崇磐，林皋.非均质地基上浅基础的极限承载力［J］.岩土工程学报，1988，10(4):4-27

［4］卢肇均.土的变形破坏机理和土力学计算理论问题［J］.岩土工程学报，1989，11(2):29-30

［5］董建国，赵锡宏.高层建筑地基基础——共同作用理论与实践［M］.上海:同济大学出版社，1997

［6］张国祥，刘宝琛.潜在滑移面理论及其在边坡分析中的应用［M］.长沙:中南大学出版社，2003

［7］李丹峰.潜在滑移线理论在求解地基危险滑面中的研究［J］.铁道勘察，2008，34(3):46-49

［8］李丹峰.基于潜在滑移线理论的地基承载力系数的研究［D］.长沙:中南大学土木建筑学院，2006

［9］Donald IB，Giam SK.Application of the Nodal Displacement Methord to Slope Stability Analysis.In:Proc 5th Australia-New Zealand Conf on Geomechanics.Sydney:Geotechnical，1998:456-460

［10］卢肇均.土的变形破坏机理和土力学计算理论问题［J］.岩土工程学报，1989，11(2):29-30

［11］陈祖煜，高峰.地基承载力的数值分析［J］.岩土工程学报，1997，19(1):6-13

［12］王勖成，邵敏.有限单元法基本原理和数值方法［M］.北京:清华大学出版社，1996

［13］高有潮，陈汀.软黏土地基塑性区开展的非线性有限元分析［J］.岩土工程学报，1983，5(2):18-24