用图论方法判断范畴的特殊对象

叶丽霞

(浙江外国语学院科学技术学院，浙江杭州310012)

1 引言

在同调代数中，范畴的始对象、终对象和零对象是非常重要的概念.

定义1［1］11设C为范畴.若I∈obC满足

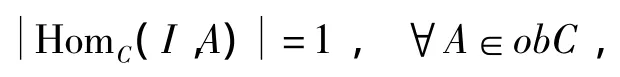
定义2［1］11设C为范畴.若I∈obC满足

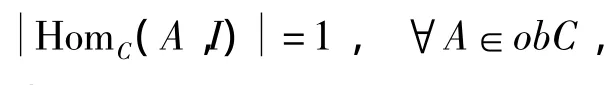
则称I为C的一个终对象.若Z同时是C中的始对象与终对象，则称Z为C的一个零对象.

定义 3［2］172设有向图 D= ＜ V，E ＞=m.令为顶点vi邻接到顶点vj的边的条数，称()n×n为D的邻接矩阵.

定义4［2］206一棵非平凡的有向树，如果有一个顶点的入度为0，其余顶点的顶点的入度均为1，则称此有向树为根树.在根树中，入度为0的顶点称为树根;入度为1，出度为0的顶点称为树叶.

定义 5［2］157设 D= ＜ V，E ＞ 为 n 阶有向图，若，即图中每个顶点的度都是0，则称D为n阶零图.特别地，1阶零图也称为平凡图.

定义6［2］162设D= ＜V，E＞为n阶有向简单图，

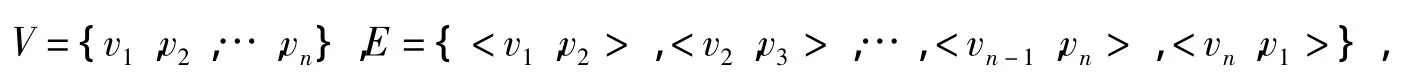
则称D为n阶圈图.

可以看出，范畴的定义比较抽象，而且范畴的始对象或终对象不一定存在.在文献［1］的例5中，作者用图来表示范畴，这样就可以相对直观地判断出范畴的特殊对象.本文利用图论知识建立了判断范畴的始对象、终对象和零对象的两个等价定理，并得到了偏序范畴等特殊范畴的相关推论.

2 主要结论及相关推论

设C为范畴，其中对象集是obC={a1，a2，…，an}.现规定obC为图的顶点集，当不同对象ai到aj存在态射时，则在两顶点之间连上一条有向边，但忽略各对象到自身的恒等态射，于是范畴C可表示为一个没有环和重边的n阶有向简单图.

定理1 设C为范畴，其中obC={a1，a2，…，an}.设图G为范畴C对应的n阶图，则有

(1)若在图G中，顶点ai到其余n－1个顶点都只有一条长度小于n的有向通路，则ai是范畴的一个始对象;

(2)若在图G中，其余n－1个顶点到顶点ai都只有一条长度小于n的有向通路，则ai是范畴的一个终对象;

(3)若顶点ai同时满足以上两个条件，则ai是范畴的一个零对象.

证明 若在范畴C对应的图G中，顶点ai到其余n－1个顶点都只有一条长度小于n的有向通路，则在范畴C中，对象ai到其余n－1个对象都只有一个态射，而ai到自身存在恒等态射，于是ai到每个对象都只有一个态射，根据定义1，ai是范畴C的一个始对象;同理，若在图G中，其余n－1个顶点到顶点ai都只有一条有向通路，则在范畴C中每个对象到ai都只有一个态射，根据定义2，ai是C的一个终对象.第三种情形显然成立.

由于任何一个有向图都有唯一的邻接矩阵，故定理1有以下一个等价定理:

定理2 设C为范畴，其中obC={a1，a2，…，an}.设图G为范畴C对应的n阶图，A为图G的邻接矩阵，令矩阵 B=A+A2+ … +An－1，则有

(1)若在矩阵B的第i行中，bii=0，该行其余元素都是1，则顶点ai是范畴C的一个始对象;

(2)若在矩阵B的第i列中，bii=0，该列其余元素都是1，则顶点ai是范畴C的一个终对象;

(3)若在矩阵B的第i行和第i列中，bii=0，第i行和第i列的其余元素都是1，则顶点ai是C的一个零对象.

当范畴对应的图是一些特殊图时，可得到相应的推论.

任意偏序集合C=(obC，≤)可看作一个范畴，其中obC的元素为对象，对象ai到aj存在一个态射当且仅当ai≤aj.把偏序关系的关系图删去所有环，就得到偏序范畴对应的图，于是有以下结论:

推论1 设C是一个偏序范畴，于是范畴存在始对象当且仅当obC存在一个最小元;范畴存在终对象当且仅当obC存在一个最大元.特别地，若范畴只有一个对象，则此对象是零对象.

证明 若ai是偏序集C=(obC，≤)的最小元，则ai≤aj对所有aj∈obC都成立.于是在范畴C对应的图中，顶点ai到其余n－1个顶点都只有一条长度小于n的有向通路，由定理1，ai是C的一个始对象.同理可证最大元就是终对象.若范畴只有一个对象，则此对象既是最小元也是最大元，从而它是零对象.

实际上，由于偏序范畴对应的图和哈斯图一一对应，因此在推论1的实际应用中，也可以根据哈斯图来判断特殊对象.在哈斯图中，若最下端的顶点只有一个，那么它就是始对象;若最上端的顶点只有一个，那么它就是终对象.在全序关系的哈斯图中，最下端的顶点就是始对象，最上端的顶点就是终对象.

例 集合obC={1，2，3，6}上的整除关系是一个偏序关系，偏序范畴C对应的图和哈斯图分别如图1中(1)、(2)所示，显然最小元1和最大元6分别是偏序范畴的始对象和终对象.

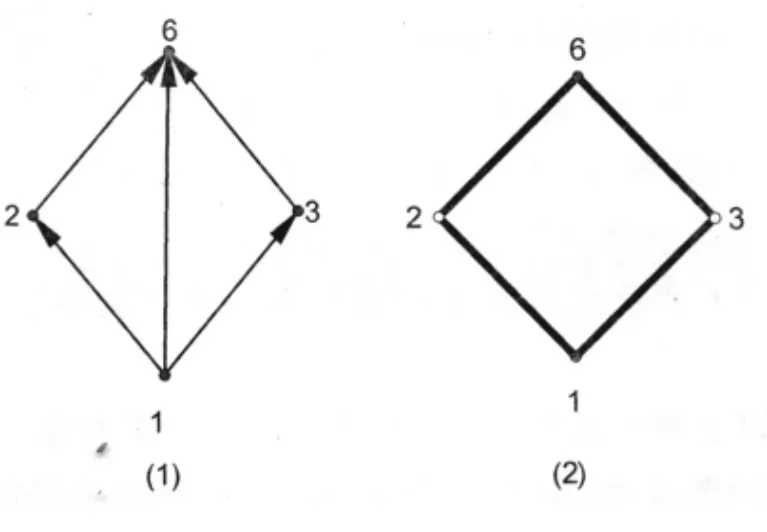
图1 偏序范畴对应的图和哈斯图

推论2 若范畴对应的图是一棵根树，则根树的树根为范畴的始对象，当且仅当根树只有一片树叶时，该树叶是范畴的终对象.另外，当根树是一棵平凡树时，它的唯一顶点是范畴的零对象.

证明 由定义4易知树根到其余顶点都只有一条长度小于n的有向通路，由定理1，树根为范畴的始对象.若根树只有一片树叶，那么其余顶点到该树叶都只有一条长度小于n的有向通路，于是该树叶是范畴的终对象.当根树是一棵平凡树时，它的唯一顶点显然是零对象.

推论3 若范畴对应的图是一个n阶零图，则当n＞1时，范畴不存在始对象和终对象;当n=1时，该唯一顶点是零对象.

证明 由定义5易知零图中的每个顶点都是孤立点，则每个顶点到其它顶点都没有通路，于是只有当n=1时，该唯一顶点是零对象.

推论4 设范畴C对应的图是一个n阶圈图，其中obC={a1，a2，…，an}，且边集E={＜a1，a2＞，＜a2，a3＞，…，＜an－1，an＞，＜an，a1＞}，则顶点 a1是零对象.

证明 由定义6，圈图的边集 E={＜a1，a2＞，＜a2，a3＞，…，＜an－1，an＞，＜an，a1＞}，则顶点 a1到每个顶点都有一条长度小于n的有向通路，根据定理1，顶点a1是零对象.

［1］佟文廷.同调代数引论［M］.北京:高等教育出版社，1998.

［2］屈婉玲，耿素云，张立昂.离散数学［M］.2版.北京:清华大学出版社，2008.