基于改进InDBSCAN算法的批量钻削工序质量增量聚类分析

周友行，董银松，张海华，郭辉

(湘潭大学 机械工程学院，湖南 湘潭，411105)

在高精度孔系类零件加工过程中，如何保证批量钻孔质量是机械加工过程的重要问题。现有批量钻削质量检测方式仍采用加工后抽检，然后对批量质量进行统计分析和评估。这种抽检方式较随意，难以对钻孔进行逐一检测，可能存在严重质量隐患。目前，对高精度孔系类零件批量钻削质量方面的研究一般采用传感器监控钻削过程，或者研发高效钻削的刀具材料以及改进钻头的结构来提高钻削加工稳定性[1−3]。钻削工序质量是对钻削过程的一种评价，与钻削过程中出现的各种现象密切相关。应用传感器监测钻削过程时，传感器信号信息丰富，而且隐含着钻削加工质量相关信息[4−7]。若能提取各钻孔工序监控信号与工序质量密切相关的数据，组成1个数据库，则通过聚类分析方法[8−10]将数据库中的数据进行分类，将批量钻孔工序分为若干类，为加工后批量钻孔工序质量的人工抽检提供理论依据，解决人工检测抽检方式随意性的问题，实时分析各工序质量的分布规律，改变切削参数，保证批量工序的加工质量。随着钻削工序的增加，批量钻削工序信号数据库中的数据也在不断变化。采用普通聚类算法时，每增加1组数据，算法都要重新检索所有的数据，重新聚类，所耗时间长，而且没有利用前一次的聚类结果信息。InDBSCAN算法其聚类结果与数据点的输入顺序无关，对噪声点亦不敏感，聚类速度较快[11−13]。因此，该算法可用来分类批量钻孔工序质量。在批量钻削工序质量检测中，钻孔加工质量合格的标准是一定的，但加工质量优秀的标准可能随钻孔工序的规模而变化。而在现有的InDBSCAN算法中，当新的数据点插入时，基本上不考虑新插入的数据在促成新类创建的同时还可能会引起已存在的不同类的合并的问题，而且在批量钻削加工工序聚类中，钻孔工序信号的数据点只增加，不删减，因此，有必要对InDBSCAN算法进行改进。此外，钻削工序监控信号数据规模相当大，直接对监控信号数据进行聚类有难度。为此，本文作者对监控信号在时域层面上进行特征提取，减小数据规模，进而利用改进的增量聚类InDBSCAN算法分析批量钻削工序质量的分布。

1 问题描述

应用声发射传感器采集批量钻削过程的声发射信号，进行24次钻削实验。实验中具体参数如下：

钻孔深度 lh=15 mm，孔径φ=6.5mm；刀尖锥度θ=130°；刀刃长度ld=1.6mm，进给量f=30 mm/min；主轴转速r=500 r/min。采集到24组钻削监控声发射(A)信号，依次编号为1～24，如图1所示。

钻削过程监控信号可描述如下：

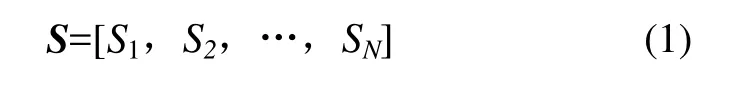
式中：Si表示第 i(i=1，2，…，N，N=24)号钻孔实验中的声发射信号向量，

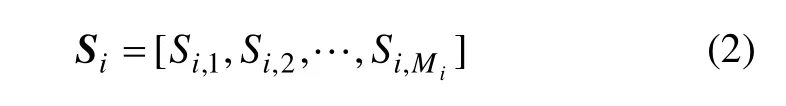
Si,j表示第i号钻孔的第j(j=1，2，…，Mi)个声发射信号采样点数值；Mi表示第i号钻孔的声发射信号采样总点数。

1.1 钻削监控信号特征提取

监控信号的数据量极大，每组信号均包含上百万个采样点。在时域层面上，对其提取特征，以特征向量来表征原数据。为了充分反映原数据的特征，对每一组钻削过程声发射信号提取均方根、均值、标准差、偏斜度和峭度共5类特征，即每组信号有5项特征属性，构成特征向量：

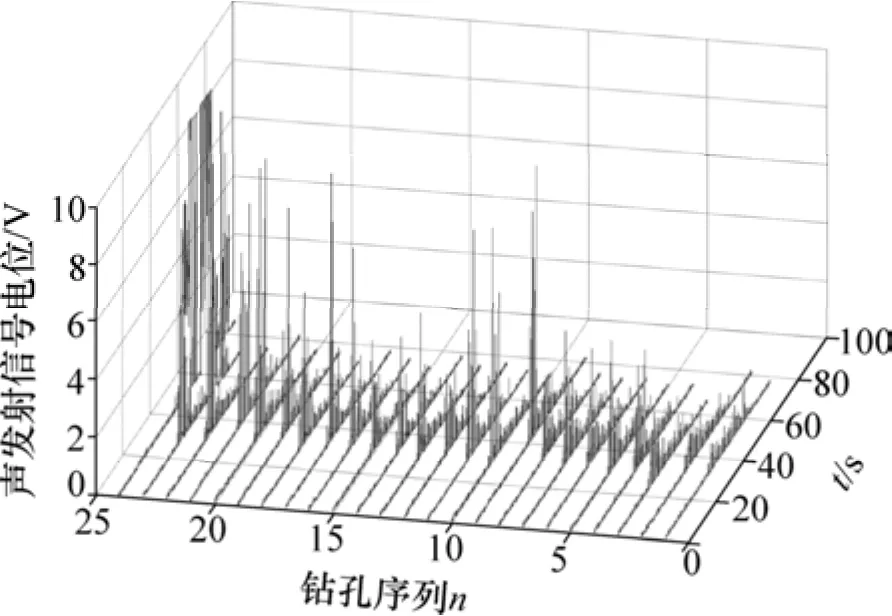
图1 24组声发射信号时域波形图Fig.1 24 groups of acoustic emission signal waveform in time-domain

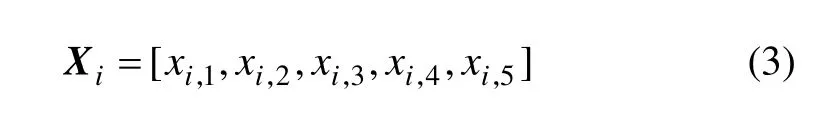
其中：xi,1为第i个钻孔监控信号的均方根，表征信号的强度；xi,2第i个钻孔监控信号的均值，反映信号的静态部分；xi,3第i个钻孔监控信号的标准差，描述信号的离散程度；xi,4第i个钻孔监控信号的偏斜度，表示信号幅值分布的不对称性；xi,5第i个钻孔监控信号的峭度，反映信号的脉动程度。

从所提取特征的数值来看，各项特征数量级存在极大差异，而这种差异会对聚类分析造成不利影响[8]。为了避免这种影响，将特征数据标准化[8]。标准化算法如下。

(1) 计算均值绝对偏差S′i：

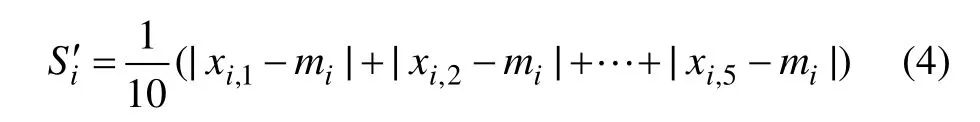
其中： xi,f(f=1,2, … ,5)为第 i(i=1，2，…，24)个钻孔的第f项特征值；mi为其5项特征值的均值，即

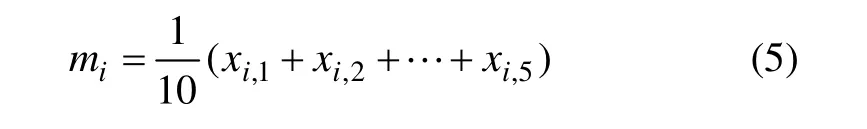
(2) 计算标准度量值：

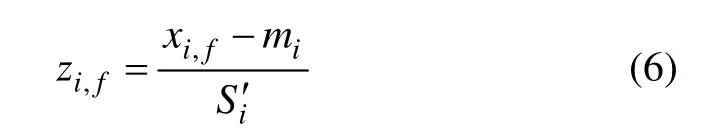
其中：f=1，2，…，5, 表示每组数据的5项特征；zi,f表示第i(i=1，2，…，24)个钻孔的第f项特征值标准化后的数值。

数据标准化后，得到批量钻削过程信号的特征向量数据库为：

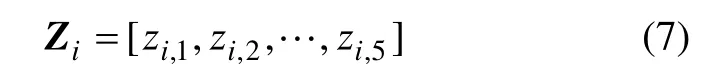
由 24组声发射信号提取出的特征向量经标准化后的特征值如图2所示。

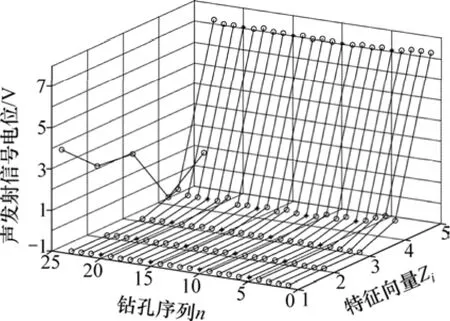
图2 24组声发射信号特征向量的标准化值Fig.2 Standardized value of characteristic vector for 24 groups of acoustic emission signal

1.2 钻削监控信号特征权重分配

在特征数据库中，上述特征值可在不同层面上反映各钻削工序特性。但在实际应用中，发现不同的特征属性对实际钻削质量的反映程度不同，其中峭度对信号中的突变特别敏感，而监控信号突变可能表示钻削故障或者钻刃崩裂等异常的发生，可明显区分钻削质量不合格的钻孔。在正常情况下，在相同钻削参数下的钻孔信号的分布应近似，则不同质量级别钻孔的信号分布差异就可由偏斜度检测出来。均方根也可反映信号的突变，但其敏感程度明显不如峭度。因此，有必要对特征向量数据库Z中的5项特征进行权重分配。本文采用层次分析法[14−15]来实现特征权重的分配。

根据层次分析法，基于实际工作经验中发现的声发射信号各特征影响钻削加工质量的相互关系，首先创建监控信号特征指标的两两判断矩阵[14]，用B={bi,j|i=1，2，…，5；j=1，2，…，5}来表示，其取值原则[14]如表1所示。

为了便于应用层次分析法，对这5特征逐一编号，f1−f5分别表示均方根、均值、标准差、偏斜度和峭度。因此，A信号特征指标的两两判断矩阵B如表2所示。

为避免人为因素造成的逻辑错误，要检验判断矩阵B的一致性，检验步骤如下。

(1) 求异性检验指标CI：

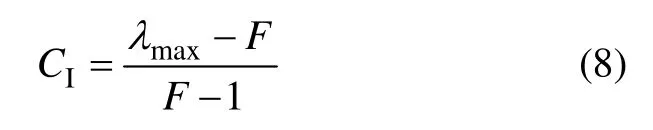
其中：λmax为判断矩阵B的最大特征值，F=5为判断矩阵的维数。计算可得 λmax≈5.237 5。则有 CI≈0.059 4。

表1 判断矩阵的标度及其含义Table 1 Scale and meaning of judgement matrix

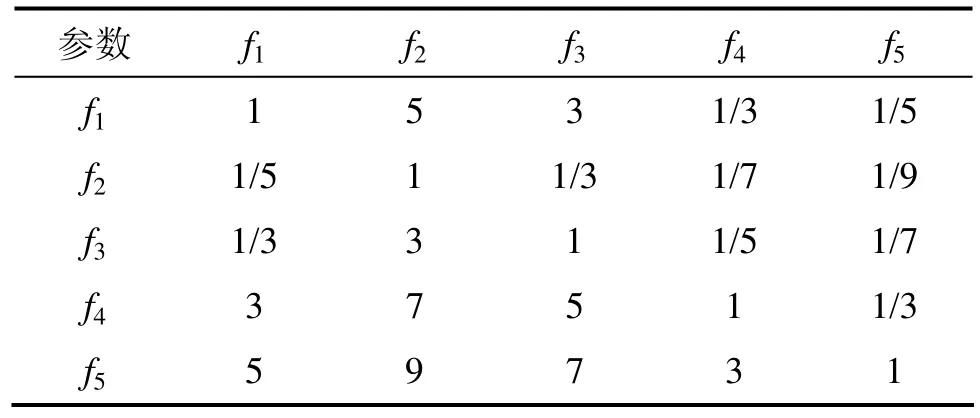
表2 A信号特征指标判断矩阵B各元素值Table 2 Element value in judge matrix B of A signal characteristic index

(2) 求平均随机一致性指标 RI。单层次判断矩阵的平均随机一致性指标 RI随矩阵的维数而变 动[14−15]，RI的取值[14]如表 3 所示。

表3 平均随机一致性指标取值表Table 3 Value of average random uniformity index

由表3可知，本例中对应F=5时，RI=1.12。

(3) 求出判断矩阵B一致性指标CR：

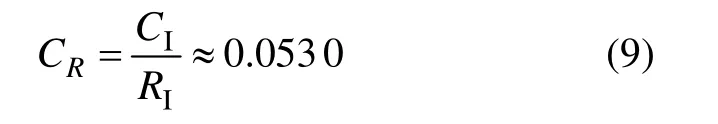
一般地，当CR≤0.1时，可以认为判断矩阵基本符合完全一致性条件，属于可以接受的程度[14−15]，可判断矩阵B一致性检验通过。取判断矩阵的最大特征值对应的特征向量，再对这个特征向量归一化处理，便可得出A信号的权值向量：

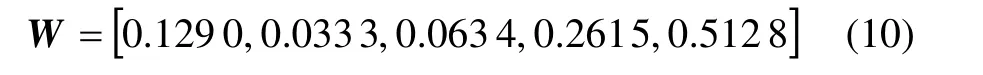
则加权后的特征向量为：

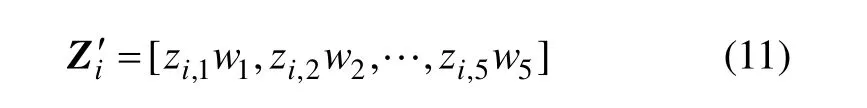
其中：wk(k=1，2，…，5)为权值向量W的第k个权值。本文中所研究的增量聚类分析方法即是以这些加权特征向量为聚类对象，实现对钻孔依据其自身质量特征的分类。

2 改进的InDBSCAN算法

InDBSCAN算法的任务就是对数据库Z中插入新数据点的情况进行增量聚类分析。这些数据点分布在高维空间中，以欧氏距离

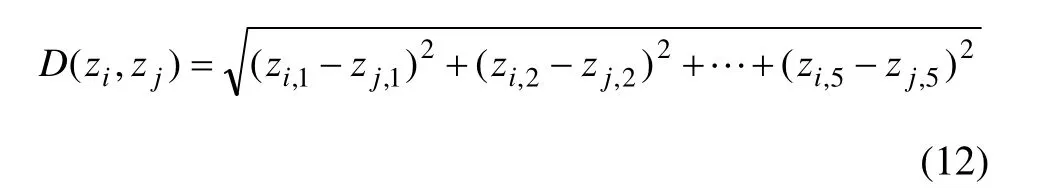
作为各数据点之间相似度的量度。其中，zi和 zj分别为24个钻孔数据点中的任意2个。该算法从改变核心状态点的邻域内包含的所有核心点开始进行处理[15]。假定新插入的数据点为P点，首先定义一类特殊点m，m 是 Z′(Z′= Z ∪ { P})中的核心点，但不是Z中的核心点，即m是由于新数据点P的插入而改变核心状态的点，m可能是1个点，也可能是多个点。那么，点m邻域内包含的所有核心点为{R}={q|q是 Z′}中的核心点，且D(q，m)≤ε}，ε为邻域半径。

以1个二维数据库为例，当最小集合点数为5时，文献[11]将数据点 P插入到数据库中所可能产生的结果分为4种，如图3所示。其中，P点以实心三角形表示，其余各点以实心圆点表示。

图3 插入数据点P时可能产生的4种聚类结果Fig.3 Four possible cluster results generated while inserting new data P

在算法设计过程中，发现还有1种情况没有被考虑，即当新插入的数据P点在促成新类创建的同时还可能会引起已存在的不同类的合并。如图4所示，在数据点P插入之前，点D是噪声，点B1和B2都是边界点。由于InDBSCAN把类定义为基于密度可达性的最大的密度相连对象的集合，所以此时 B1和 B2分别属于2个不同的聚类C1和C2，且D点及其邻域内的噪声点不属于任何一个聚类。当数据点P插入之后，点D，B1和B2由于其邻域内的数据点数均同时达到最少点数目的要求而转变为核心点，但P点由于其邻域内的数据点数小于最少数目而不是核心点，所以创建以D为核心点的新类。此时，由于点B1和B2新建立起来的相互之间的直接密度可达性，而使类 C1和 C2中的所有数据点相互成为了密度相连对象，2个聚类合并。如果在这种情况下只考虑到以D点为核心点的新类的创建，那么就会忽略掉C1和C22个已有类的合并，从而造成本应在同一类中的数据点的分离，在本文的应用中，就是造成质量属性相近的孔被分到了2个不同的类中。反之，如果只考虑到2个已有类的合并，那么，本应归入新类中的数据点却仍然被当作噪声点。如果算法没有考虑这种情况，那么当数据点的输入顺序不同时，就可能会产生不同的聚类结果，即算法会与数据的输入顺序有关，从而使结果具有不确定性。

图4 创建新类的同时合并已有类Fig.4 Clusters merge while new cluster being created

3 钻削信号的增量聚类分析

3.1 InDBSCAN增量聚类

分别使用 2种方法(原有的和改进的 InDBSCAN算法)对24组钻削过程特征向量进行1.0×105次增量聚类，每一次的特征向量输入顺序均为随机生成。结果表明，在这 1.0×105次增量聚类中，改进的InDBSCAN算法只产生同1种聚类结果(如表4所示)，而原有的InDBSCAN算法则产生了2种聚类结果(如表5和6所示)。

由表4～6可知，类别0中的数据点为噪声点。由表5和6可知，使用原有的InDBSCAN对24组钻削过程特征向量进行增量聚类，根据特征向量输入顺序的不同，会产生不同的聚类结果。在表6所示的聚类结果中，产生了忽略掉已有类合并的情况，即把本应属于第1类的第10，12，14和15个钻孔的特征向量数据点作为一个单独的类分离了出来。

表4 改进的InDBSCAN增量聚类结果Table 4 Incremental clustering results of improved InDBSCAN

表5 原有的InDBSCAN增量聚类结果(No.1)Table 5 Incremental clustering results (No.1) of original InDBSCAN

表6 原有的InDBSCAN增量聚类结果(No.2)Table 6 Incremental clustering results (No.2) of original InDBSCAN

3.2 聚类结果评价

3.2.1 聚类结果准确率分析

采用准确率对聚类结果进行评价[16]。准确率可以表示聚类结果的准确程度，其值越高，聚类结果与实际结果越接近。为了对改进的InDBSCAN算法增量聚类分析结果的准确率做出评价，对24个钻孔依次进行人工常规质量检测，其检测结果如表7所示。

表 7中，A′类为质量优良的钻孔，B′类为合格产品，C′类为不合格产品。在24号孔的钻削过程中，钻花发生严重崩刃，钻削没有继续进行。23号钻孔内表面刮伤严重。

由算法聚类所得到的钻孔分类，只是把不同质量级别的钻孔区分开，而不能确定具体某一类的质量级别。因此，确定聚类结果的类别与人工分组的映射关系是必要的。在这里，利用信息检索中的 F-measure方法[16]来实现这一点。F-measure方法综合信息检索中的查准率和查全率的思想对聚类结果进行评价，含义如下。

表7 批量钻削工序质量人工检测结果Table 7 Manual inspection results of batch drilling-quality

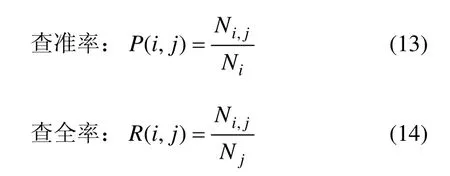
其中：i=A′，B′，C′，表示人工分组结果；j=0，1，2表示算法聚类的分类结果；Ni,j表示聚类j中分组i的数目；Ni为分组i中所有对象的数目；Nj为聚类j中所有对象的数目。分组i的F-measure值定义为：

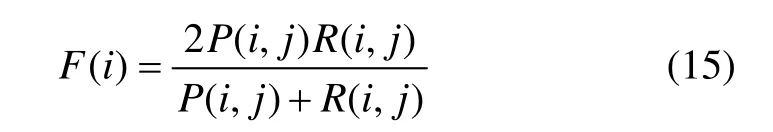
对分组i而言，哪个聚类j的F-measure值高，就认为该聚类 j是分组 i的映射计算结果，InDBSCAN算法聚类结果类别1即是人工分组A′的聚类映射，相应地，类别2是分组B′的聚类映射，类别0是分组C′的聚类映射。下面，通过2个步骤来计算聚类的总体准确率。

(1) 计算各个聚类的准确率Pk：

其中：Nk为InDBSCAN聚类结果类别k包含钻孔的个数；Rk为类别k中钻孔序号与此类别相应的人工分组中序号相同的个数，k=0, 1, 2。

(2) 计算聚类的总体准确率PG：

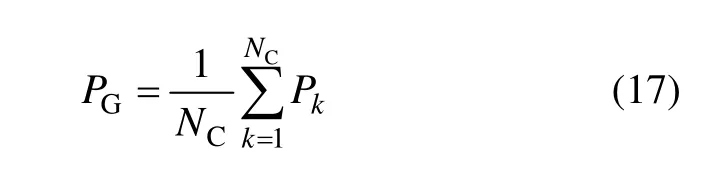
其中：NC=3为InDBSCAN算法聚类结果的类别数。计算可得，本次试验的聚类总体准确率为84.03%。

3.2.2 聚类结果离群点分析

从表3和表6的分类标识来看，人工检测出的23号、24号不合格孔，在InDBSCAN聚类结果中也同样从其他合格的聚类中分离出来。由此看出，InDBSCAN具有很高的离群点检测性能。这样，在钻削加工的在线监测中，只要有不合格孔产生，都会被及时检测出来，然后采取相应的措施，以避免更大的损失出现。

4 结论

(1) 由于改进的InDBSCAN考虑到了数据点插入时可能产生的所有情况，由此算法所得结果与数据输入顺序无关。

(2) 使用增量聚类方法对钻削过程信号进行分析，可有效实现批量钻削工序质量分布的分析。该方法可为批量钻削工序质量的逐一无损在线检测提供新思路和理论基础。

[1]XU Xu-song, Cao YAN-long, YANG Jiang-xin. Condition monitor of deep-hole drilling based on multi-sensor information fusion[J]. Chinese Journal of Mechanical Engineering, 2006,19(1): 140−142.

[2]Kim D W, Lee Y S, Park M S. Tool life improvement by peck drilling and thrust force monitoring during deep-micro-hole drilling of steel[J]. International Journal of Machine Tools &Manufacture, 2009, 49(3/4): 246−255.

[3]Rivero A, López de Lacalle L N, Luz Penalva M. Tool wear detection in dry high-speed milling based upon the analysis of machine internal signals[J]. Mechatronics, 2008, 18(10):627−633.

[4]邵忍平, 黄欣娜, 胡军辉. 聚类分析的数据挖掘方法及其在机械传动故障诊断中的应用[J]. 航空动力学报, 2008, 23(10):1933−1938.SHAO Ren-ping, HUANG Xin-na, HU Jun-hui. Analysis of data mining of clustering and its application to mechanical transmission fault diagnosis[J]. Journal of Aerospace Power,2008, 23(10): 1933−1938.

[5]ZHOU You-hang, ZHANG Jian-xun. Analysis of Relationship between batch drilling process and Multi-Sensor Synchronization Signals[C]//Proceedings of International Conference on Measuring Technology and Mechatronics Automation, 2009: 127−130.

[6]周友行, 张建勋, 唐稳庄. 基于瞬态特征的钻削过程与监控信号映射模型[J]. 中南大学学报: 自然科学版, 2010, 41(3):971−976.ZHOU You-hang, ZHANG Jian-xun, TANG Wen-zhuang.Mapping between phases and signals in drilling process based on transient features of signals[J]. Journal of Central South University: Science and Technology, 2010, 41(3): 971−976.

[7]Singh R, Khamba J S. Comparison of slurry effect on machining characteristics of titanium in ultrasonic drilling[J]. Journal of Materials Processing Technology, 2008, 197(2): 200−205.

[8]Han J W, Kamber M. 数据挖掘: 概念与技术[M]. 范明, 孟小峰, 译. 2版. 北京: 机械工业出版社, 2007: 251−301.Han J W, Kamber M. Data Mining: Concepts and Techniques(Second Edition)[M]. FAN Ming, MENG Xiao-feng,translate. 2nd ed. Beijing: China Machine Press, 2007: 251−301.

[9]邓冬梅, 龙际珍, 尹湘舟. 一种结构化 Web文档的联合聚类算法[J]. 中南大学学报: 自然科学版, 2010, 41(5): 1871−1876.DENG Dong-mei, LONG Ji-zhen, YIN Xiang-zhou. A co-clustering algorithm based on structured Web document[J].Journal of Central South University: Science and Technology,2010, 41(5): 1871−1876.

[10]HU Rui-fei, YIN Guo-fu, TAN Ying. Cooperative clustering based on grid and density[J]. Chinese Journal of Mechanical Engineering, 2006, 19(4):544−547.

[11]Ester M, Kriegel H-P, Sander J, etc. Incremental Clustering for Mining in a Data Warehousing Environment[C]//Proceedings of 24th International Conference on Very Large Data Base. New York: USA, 1998: 323−333.

[12]Ester M, Kriegel H P, Sander S, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the Second International Conference on Knowledge Discovery and Data Mining. Portland, USA, 1996:226−231.

[13]徐新华, 谢永红. 增量聚类综述及增量DBSCAN聚类算法研究[J]. 华北航天工业学院学报, 2006, 16(2): 15−17.XU Xin-hua, XIE Yong-hong. Summarization on incremental clustering and research of incremental DBSCAN algorithm[J].Journal of North China Institute of Astronautic Engineering,2006, 16(2): 15−17.

[14]王新民, 赵彬, 张钦礼. 基于层次分析和模糊数学的采矿方法选择[J]. 中南大学学报: 自然科学版, 2008, 39(5): 875−880.WANG Xin-min, ZHAO Bin, ZHANG Qin-li. Mining method choice based on AHP and fuzzy mathematics[J]. Journal of Central South University: Science and Technology, 2008, 39(5):875−880.

[15]DONG Yu-chen, ZHANG Gui-qing, HONG Wei-chiang, et al.Consensus models for AHP group decision making under row geometric mean prioritization method[J]. Decision Support Systems, 2010, 49(3): 281−289.

[16]杨燕, 靳蕃, 等. 聚类有效性评价综述[J]. 计算机应用研究,2008, 25(6): 1630−1632.YANG Yan, JIN Fan, et al. Survey of clustering validity evaluation[J]. Application Research of Computers, 2008, 25(6):1630−1632.