基于线性回归-马尔可夫模型的铁路客运量预测

李晓东

（沈阳铁路局 沈阳客运段，辽宁 沈阳 110013）

我国经济的快速发展、社会的进步改变了人们的工作方式和生活习惯，同时也改变了对运输的需求。旅客的经济能力和时间价值观念逐渐增强，更加关注运输质量，包括出行的便捷性、旅行的舒适性、旅行时间的缩短、安全性的提高、运输服务水平等[1]。目前，铁路运输面临着运输数量和质量的双重压力。为解决铁路运输的“瓶颈”问题，我国进行了既有线提速和高速铁路建设，预计 2012年投产新线 6 366 km。“十二五”期间，全国铁路运营里程将达到12万 km，其中以高速铁路为主骨架的快速铁路网达4.5万 km，西部地区铁路达 5万 km。这将使铁路既有的优势得以充分发挥，同时也为铁路的发展注入新的活力。

1 客运量预测模型的选择

铁路客运量既是衡量运营效果的一项重要指标，运输部门可以根据客运量的变化及时调整战略部署，同时也是铁路项目可行性研究中的重点内容，是论证项目建设必要性和经济性的基础。国内外采用的铁路客流量预测方法较多，其中定量预测方法可分为因果关系分析法、产运销平衡法、四阶段法等。这些方法在预测精度上都有待提高，以便为决策者提供更可靠的数据。在铁路既有线提速前，客运量预测只是针对趋势客运量。但是，既有线实施提速和高速铁路建成投入运营，铁路客运综合服务质量得到提高，如果照搬某一种方法，预测结果将会出现偏差，并且随着时间的推移，理论预测值和未来实际运量的误差也会越来越大[2]。

回归分析是一种应用极为广泛的数量分析方法，主要用于确定2种或2种以上变量间相互依赖的定量关系。回归分析的基本思想是：虽然自变量和因变量之间没有严格的、确定性的函数关系，但可以设法找出最能代表它们之间关系的数学表达形式。因此，可以通过因变量和自变量来确定变量之间的因果关系，建立线性回归模型，并根据实测数据求解模型的各个参数，然后评价回归模型是否能够很好地拟合实测数据，如果能够很好地拟合，则可以根据自变量作进一步预测[3-4]。

线性回归预测模型对经济社会系统预测具有重要的意义，但由于客运量的影响因素复杂，其变化呈现一定的随机波动特点，因而预测结果会产生误差。而马尔可夫链是根据系统状态之间的转移矩阵来描述一个随机动态系统未来的发展状态，转移矩阵反映了各个状态之间的规律性。马尔可夫链过程最主要的特征就是无后效性，即t时刻之后的状态只与 t时刻的状态有关，而与以前的状态无关。因此，可以通过对线性回归预测模型的结果进行马尔可夫链改进来提高其预测的准确性[5]。

2 铁路客运量预测

2.1 线性回归模型确定预测值

铁路客运量的影响因素包括国民生产总值、人口数量、居民消费水平、运价、运输服务水平、运输方式结构等。目前，国家制定了“十二五”规划，但以上因素仍存在一定的不确定性。因此，选取铁路营业里程这一相对确定的指标进行线性回归分析。2001—2010年我国铁路客运量和铁路营业里程如表1所示[6]。根据数据作散点图，其趋势大致呈线性关系，如图1所示。

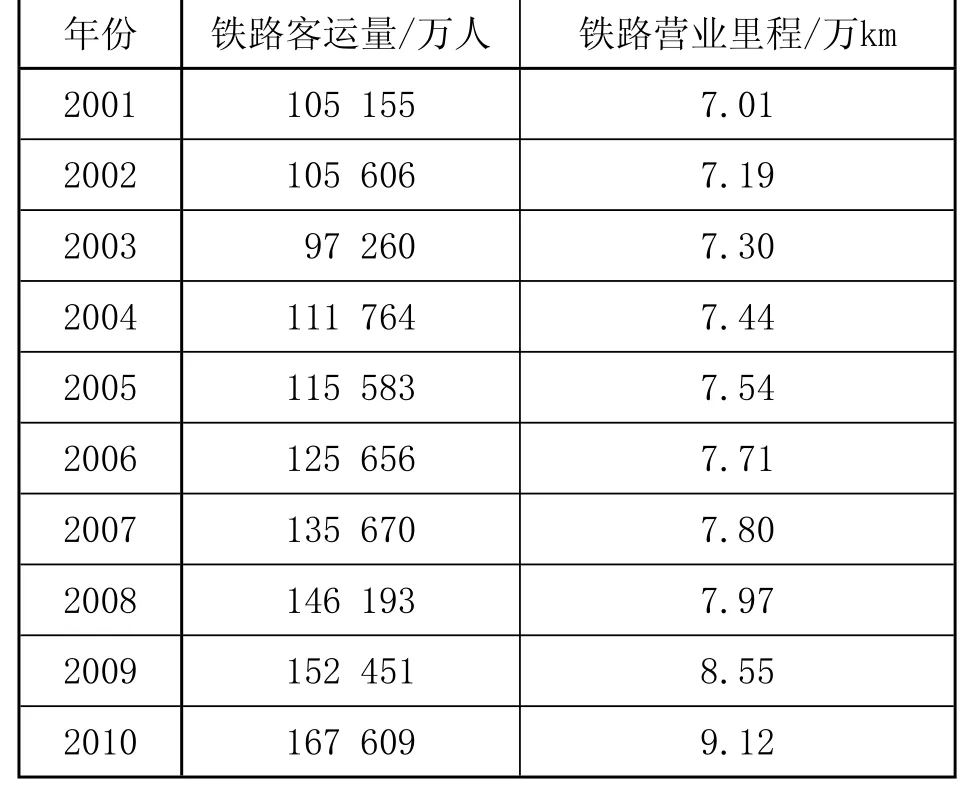
表1 2001—2010年全国铁路客运量和铁路营业里程

图1 2001—2010年全国铁路客运量和铁路营业里程关系散点图

按数据趋势可以建立线性方程，应用 MATLAB 软件，回归方程为：

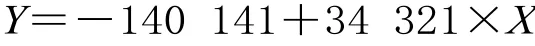
式中：X 为营业里程，万km；Y 为铁路客运量，万人。

回归模型拟合度检验结果显示，相关系数为0.950，而决定系数 R2为0.903，回归方程对样本数据点拟合较好。

根据公布的数据：2011年铁路新增线路 2 022 km，2012年计划新增线路 6 366 km，2015年计划铁路线路全长达到 12万 km。根据上述公式可以得到铁路客运量的回归预测值及相对误差，如表2所示。

表2 铁路客运量回归预测相关数据

2.2 回归-马尔可夫预测模型确定预测值

马尔可夫链是根据系统状态之间的转移矩阵来描述一个随机动态系统未来的发展状况，转移概率(即在事件的发展变化过程中，从某一种状态出发下一时刻转移到其他状态的可能性) 则反映了各状态之间某种内在的规律性。其中，n 步状态转移矩阵的计算为：

P(n) 描述了 m个状态相互转移的概率分布。其中，pij为由状态 i 转移到状态j 的概率[7-8]。如 p12表示由状态1转移到状态2的概率。下一时刻向各状态转移的概率 P(E) 为：

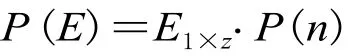
其中 E1×z是一个1行 z 列的矩阵，为当前时刻的状态矩阵，z 为划分的状态区间。

回归—马尔可夫预测模型的基本思想是先用回归预测模型进行预测。然后根据回归预测数据与原始数据的相对误差将各原始数据年划分状态。再根据各年所处状态求得状态转移矩阵，进行未来相关数据的预测。

2.2.1 状态划分

根据表2中的相对误差列，将原始数据按年划分为4个状态，划分标准如表3所示。例如，2009年的回归预测相对误差为 0.56%，则该年属于状态 3。

表3 状态划分区间及各状态含义

2.2.2 状态转移

铁路客运量在 2001—2010年中各类状态的一步转移情况如表4所示。例如，表4中第二行的数据含义为：由状态 1一步转移到状态1和一步转移到状态3的情况各出现了1次，合计为2次。表4中的其他数据依次类推。

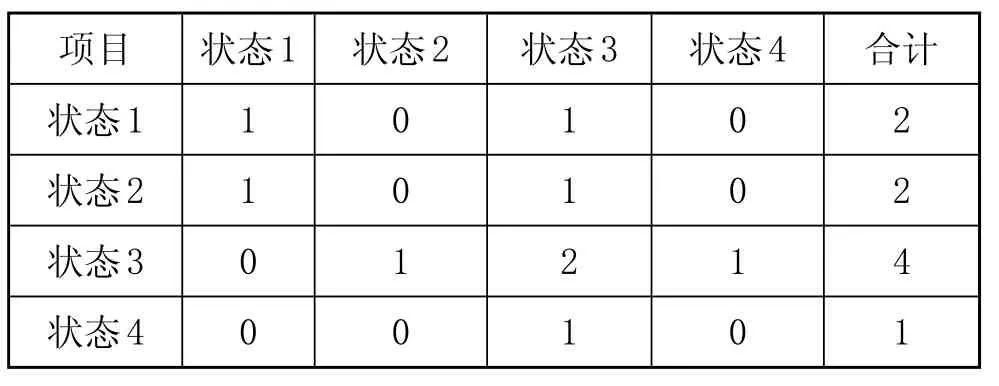
表4 回归预测结果马尔可夫状态转移

2.2.3 数据预测

根据 2001—2010年铁路客运量数据，以2010年为当前时间点预测 2011年铁路客运量，需要计算一步状态转移矩阵；预测 2012 与 2015年的铁路客运量，需要分别计算二步状态转移矩阵与五步状态转移矩阵。下面以运用回归—马尔可夫模型预测2011年铁路客运量为例，说明该模型的具体计算过程。

从状态的转移表可确定马尔可夫一步状态转移矩阵P (1)。

由于 2010年铁路客运量所处的状态为状态 3，对应 2010年的状态矩阵为 (0，0，1，0)，因而 2011年铁路客运量转向各状态的概率为：

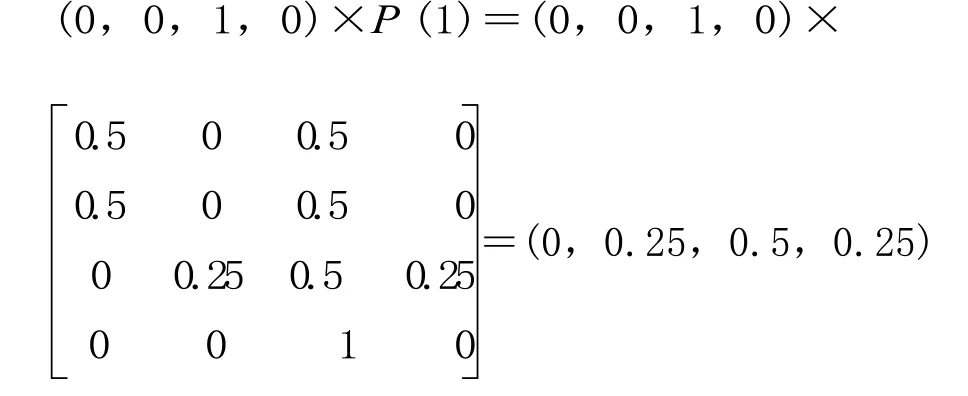
即 2011年铁路客运量有 0.25 的概率处于状态2和状态 4，有 0.5 的概率处于状态 3。

由各状态区间的预测中值，分别乘以预测年可能处于该状态的概率再求和，即：175 238×0.25＋184 225×0.50＋196 806×0.25＝185 124(万人)，得到 2011年铁路客运量回归—马尔可夫预测值为185 124万人。同理，计算得到 2012年和 2015年铁路客运量的预测结果，如表5所示。

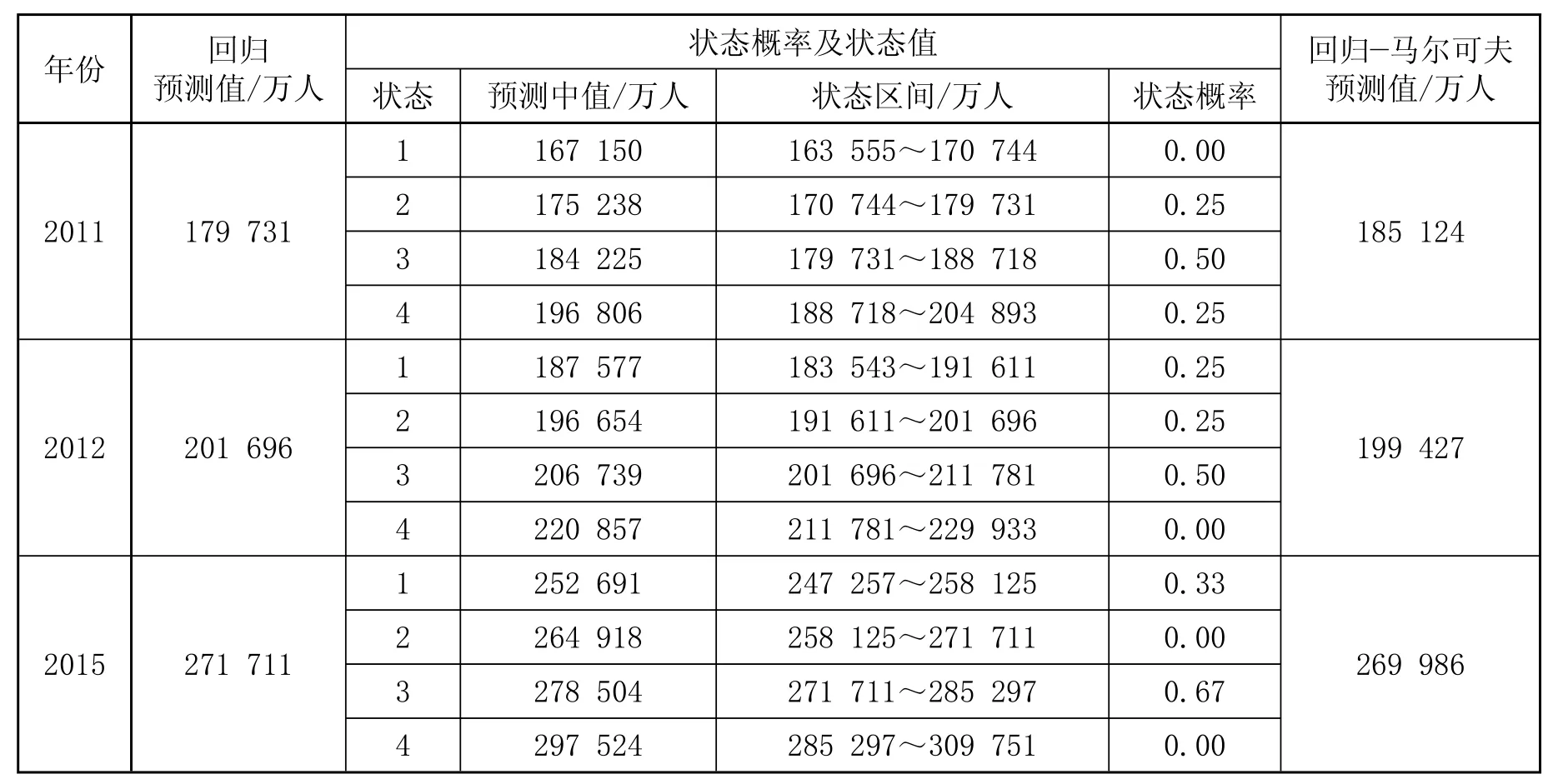
表5 铁路客运量回归-马尔可夫预测值

3 结束语

基于回归—马尔可夫预测模型的 2011年、2012年铁路客运量预测值分别为 185 124万人和 199 427万人，与 2011年实际数据和 2012年预计数据的误差为-0.04% 和 -1.72%。因此，在铁路客运量预测方面，对线性回归预测模型结果进行马尔可夫链改进的方法能够提高预测的准确性。但还需通过更多的实际数据对预测模型的可靠性进行验证，以不断完善回归—马尔可夫预测模型。

[1]郭孜政. 铁路客运量影响因素层次结构分析[J]. 交通运输工程与信息学报，2007(4)：68-71.

[2]王传峰. 既有线提速后的客运量预测研究[D]. 四川：西南财经大学，2008.

[3]侯丽敏，马国峰. 基于灰色线性回归组合模型铁路客运量预测[J]. 计算机仿真，2011(7)：1-3，30.

[4]谢孝如，蒋惠园，申耀伟. 基于并联灰色—线性回归组合模型的客运量预测[J]. 铁道运输与经济，2008(8)：92-94.

[5]田自力，刘碧发. 灰色马尔可夫链预测模型[C]. 台湾第一届灰色系统理论与应用研讨，1996：157-161.

[6]国家统计局. 中国统计年鉴：1999—2011 [M]. 北京：中国统计出版社，1999—2011.

[7]关 静. 中国民航旅客吞吐量的灰色马尔可夫模型预测[J].中国民航大学学报，2010(2)：45-47.

[8]张 诚，张广胜. 基于优化灰色—马尔可夫链模型的铁路货运量预测[J]. 物流技术，2011(13)：129-142.