基于灰色系统理论的车站通过能力计算方法研究

方 惠，王慈光，赵 亮

(西南交通大学 交通运输与物流学院，四川 成都 610031)

车站是铁路网中的节点，是铁路运输的基层生产单位。车站的工作质量对于提高铁路运输安全正点、运输效率和经济效益具有重要的作用。为了较好地组织运输生产活动，满足日益增长的运输需求，车站应当具有相应的能力。车站能力包括通过能力和改编能力，通过能力分为咽喉通过能力和到发线通过能力，改编能力分为解体能力和编组能力。车站 (主要指技术站) 通过能力是指在现有设备条件下，采用合理的技术作业过程，一昼夜能够接、发的货物列车数和旅客列车数[1]。

目前，车站能力的计算方法主要有图解计算法、计算机模拟法和分析计算法。长期以来，国内外许多专家、学者进行了较深入的研究，并提出了数学模型和求解算法[2-6]。这些理论成果为车站能力计算方法的优化奠定了基础。但是，能力的各种计算方法和测定手段复杂多样、相互独立，而且有的计算结果和实际运用差别较大，甚至出现某些情况下车站能力利用率超过 100%的所谓“超能力”现象。为此，在相关研究成果的基础上，基于灰色系统理论，运用数理统计知识，以咽喉通过能力为对象，提出车站能力的区间表示法及计算步骤。

1 传统的咽喉通过能力计算方法

传统的咽喉通过能力计算办法是，首先计算各道岔组一昼夜进行各项作业的总占用时间 T。

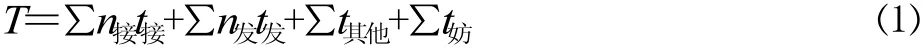
式中：n接，n发为一昼夜占用道岔组的接、发列车数(客、货、单机分开)；t接，t发为接、发车占用咽喉时间标准 (分为为扣除接、发列车外的所有其他作业(包括机车出入段、其他调车作业)占用道岔组的总时间；∑t妨为直接妨碍时间。

其次，将负荷量最大 (即 T 最大) 的道岔组确定为咽喉道岔组，采用式⑵计算咽喉道岔组通过能力利用率 K：

式中：γ空费为考虑咽喉道岔组的空费时间和间接妨碍时间扣除的系数，可采用 0.15~0.20；∑t固为固定作业时间，包括旅客列车到发及本务机车出入段，调车机车出入段等作业。

最后，计算车站各衔接方向咽喉道岔组的通过能力：

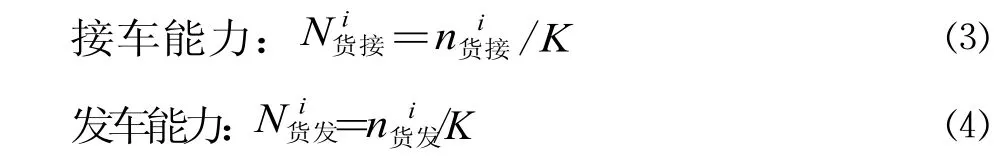
2 弱化缓冲算子及灰度计算原理

2.1 弱化缓冲算子

为了求得各项作业占用道岔组的时间标准，传统方法是计算实测数据样本的平均值，以此作为该项作业时间标准。但原始数据往往波动较大，而且常有异常值出现，使结果的准确性受到影响。因此，有必要采用灰色系统理论中的加权弱化缓冲算子[6]先对数据样本的波动进行弱化，然后再确定时间标准。

占用道岔组作业时间的实测数据样本数据序列属于冲击扰动序列，称为 X，是占用道岔组真实时间数据序列 X(0)受冲击扰动项干扰后产生的。从理论上说，占用道岔组作业的时间数据变动幅度应当较小，总体趋于平稳。但由于人为及其他各种因素的影响，例如，车站值班员信号开放时间的早晚或列车进站速度的快慢等，实测的时间数据序列X波动较大，不符合数据的真实变化规律，因而需要对X的变动幅度进行弱化处理。

采用弱化算子对数据序列进行弱化处理时需要考虑以下3个方面问题。

（1）不动点设置。根据缓冲算子不动点公理[6]，需要设置一个不动点 x(n)，使得运用序列算子 D 对数据进行调整时不改变 x(n) 的值，即 x(n)d＝x(n)。本文采用原始时间数据的均值作为不动点 x(n)。

（2）原始数据序列的处理。弱化算子可以对增长序列、衰减序列和振荡序列进行弱化。由弱化算子的定义[6]可知，弱化算子可以使增长序列和衰减序列的整体变化速度减缓，振荡序列的峰值减小、谷值增大。设 D 为弱化算子，则有：

X 为增长序列：x(k)≤x(k)d，k＝1，2，…，n

X 为衰减序列：x(k)≥x(k)d，k＝1，2，…，n

X 为振荡序列：

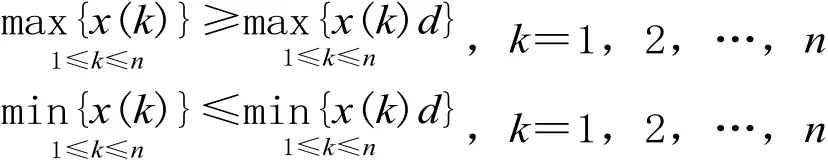
对于占用道岔组的时间数据序列，适于采用整体变化速度减缓的弱化方法。根据不动点公理，在序列弱化处理前需要将原始数据序列处理成增长与衰减序列。

（3）弱化算子的选择。常用的弱化算子有平均弱化缓冲算子、加权平均弱化缓冲算子[6]。设原始数据序列为 X＝[x(1)，x(2)，…，x(n)]，令弱化序列为 XD＝[x(1)d，x(2)d，…，x(n)d ]，各时点的权重为 W＝[w1，w2，…，wn]，则有

D 为平均弱化缓冲算子：

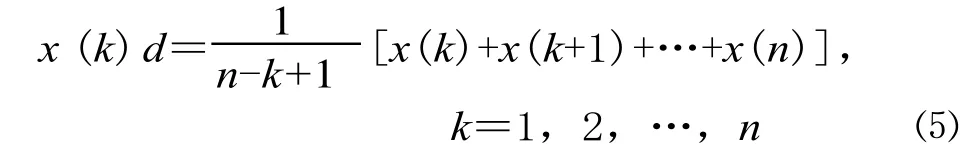
D 为加权平均弱化缓冲算子：

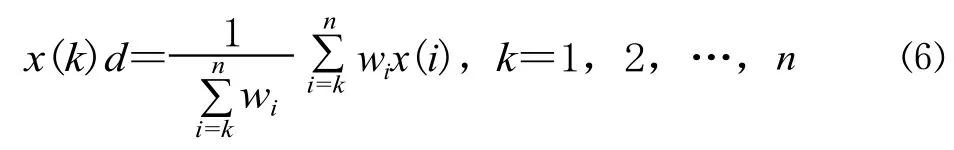
针对占用道岔组的时间数据越偏离均值频数越低这一规律，宜采用加权平均弱化缓冲算子。权重的取值为各时间数据的频数。

2.2 灰度

通过对车站连续3个昼夜作业跟踪写实而收集到的数据样本，不可避免地存在很多不确定因素，传统的用样本均值作为总体均值的估计值得到的结果与真实情况往往存在偏差，根本无法保证由此算得的能力的可靠性，现场常常出现“超能力”现象就是从反面说明这一方法不够科学。采用区间估计意味着在一定的概率下，数据取值可以在一定范围内变动，能力也以一定概率落入某一区间，这样的计算和表示方法将更为科学与合理。

区间估计后，本文将数据区间视为灰数，用灰数的灰度[6]来刻画数据区间的精确度。灰度是灰数产生背景或论域与灰数取数域测度的比值。在计算占用道岔组的作业时间标准的灰度时，将原始数据的取值范围作为论域，将数据估计区间的长度作为取数域测度，两者的比值即为灰度，由此得到式⑺：

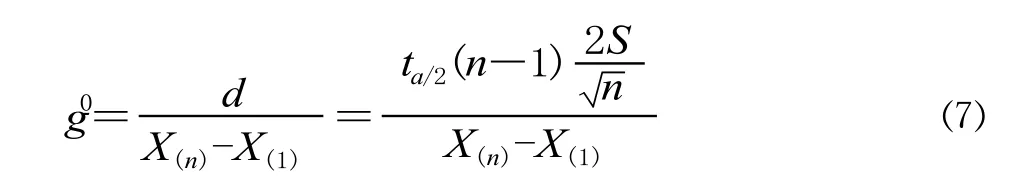
式中：d 为参数估计区间的长度；X(1)，X(n)分别为原始数据样本中最小次序统计量与最大次序统计量，tα/2(n－1) 为置信度为 α/2、自由度为 n－1 的 t 分布的临界值，S 为样本标准差，n 为样本量。

灰度的取值范围为[0，1]。灰度越大，表示精确度越低，反之精确度越高。灰度为零时为白数，白数是完全确定的数，没有任何不确定成分；灰度为1时，为灰度的最大值 ，表示灰数覆盖了灰数产生的背景或论域，故不含任何有用的信息。针对道岔组通过能力的计算，灰度取 0.15 可认为达到精确度要求。

3 计算步骤

步骤 1：从原始数据写实表中提取某项作业占用道岔组时间t的原始数据序列，计算其均值t 。

步骤 2：将实测时间数据按由小到大进行排序，剔除重复数据项后形成数据序列 X＝[x(1)，x(2)，…，x(n)]。以序列 X 中各数据相应的频数作为权重向量 W＝[w1，w2，…，wn]。

步骤 3：以t为界，将数据序列X分为两部分，再分别加上不动点t形成增长序列 XL和衰减序列XU。的权重系数取值为：wt＝max{w1，w2，…，wn}

则 XL、XU 相应的权重取值为：

步骤 4：采用式⑹的加权弱化缓冲算子对 XL、XU 进行弱化，生成弱化序列 XLD 和 XUD。

步骤 5：用 XLD 和 XUD 中的数据代替原始序列中的相应数据，形成新序列，计算新序列的均值 μ在置信水平 (1－α) 下的置信区间：

步骤 6：用式⑺计算该置信区间的灰度，将该项作业占用道岔组的时间标准表示为 [tL，tU]g0。若灰度值不满足要求，返回步骤 4，否则，执行下一步。

步骤 7：从步骤1至步骤6逐一确定出接发车占用咽喉时间标准 t接客，t发客，t接货，t发货，t接单，t发单的置信区间和灰度后，代入式⑴计算各道岔组总占用时间 T。

步骤 8：用 NSG 可能度排序计数法[8]比较各道岔组总占用时间 [tL，tU]的大小。首先用 NSG 可能度计算公式 (如式⑽所示) 计算任意两个道岔组占用时间区间数一个大于等于另一个的可能度，得到可能度矩阵(pij)N×N，其中pij＝p([tLi，tUi]≥[tLj，tUj])。然后统计第 i 行大于 0.5 的元素个数，记为 ni，i＝1，2，…，N。最后对 ni进行排序，若有ni1≥ni2≥…≥niN，则可得排序结果 [tL1，tU1]≥[tL2，tU2]≥…≥[tLN，tUN]。

步骤 9：将负荷量最大 (即 T 最大) 的道岔组确定为咽喉道岔组，将咽喉道岔组的 T 代入式⑵计算咽喉道岔组利用率：

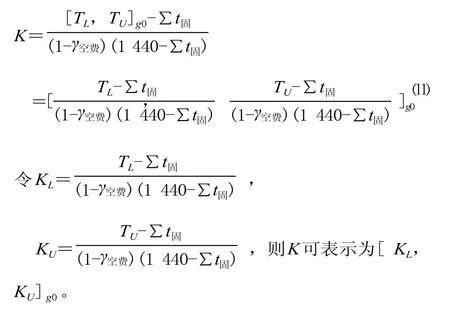
将咽喉道岔组利用率 K 和车站该衔接方向的实际接发车数量代入式⑶、式⑷，便可计算出车站该衔接方向咽喉通过能力。

4 算例

以成都铁路局密地站某年的能力查定资料为例。根据3个昼夜采集的原始数据，用本文提出的方法计算该站渡口方向咽喉通过能力，具体步骤如下。

步骤 1：对原始数据按接车、发车及其他作业占用进行分类。接发货物列车和单机占用咽喉道岔时间的原始数据如图1所示。渡口方向接发旅客列车数量很少，可直接采用均值作为t接客，t发客的时间标准。以渡口方向办理货物列车到达作业时间标准的确定为例进行了说明，的确定方法类似。

图1 渡口方向4项作业原始数据频数分布直方图

步骤 2：序列的生成与权重系数的确定。实测采集到的渡口方向办理货车到达作业时间数据原始序列为：[10，11，11，10，8，9，8，14，12，18，9，10，6，8，15，12，9，13，10，8，9，8，11，14，4，10，8，14，5，12，9，8，11，8，16，11，5，10，9，7，12，12，7，16，12，13，10，10，8，9]，共计 50 项。将实测数据由小到大排序，剔除重复项后形成数据序列 X＝[4，5，6，7，8，9，10，11，12，13，14，15，16，18]，权重向量为 W＝ [1，2，1，2，9，7，8，5，6，2，3，1，2，1]。实测时间数据均值为t=10.18，取权重系数为{1，2，1，2，9，7，8，5，6，2，3，1，2，1}＝9。以均值 10.18 为界，形成增长序列 XL＝[4，5，6，7，8，9，10，10.18]和衰减序列 XU＝[18，16，15，14，13，12，11，10.18]，权重向量分别为[1，2，1，2，9，7，8，9]和[1，2，1，3，2，6，5，9]。

步骤 3：加权弱化。采用式⑹对 XL、XU 进行一阶弱化。一阶弱化后用新值代替原始数据中对应的数据，计算标准差 S＝0.90。序列 X 变化为 XD＝[8.73，8.86，9.07，9.16，9.29，9.78，10.10，10.47，10.93，11.12，11.46，11.60，11.92，12.12]。计算数据如表1所示。

采用序列 XD 中的数值代替原始序列相应的数值，形成序列 XN＝[10.10，10.47，10.47，10.10，9.29，9.78，9.29，11.46，10.93，12.12，9.78，10.10，9.07，9.29，11.60，10.93，9.78，11.12，10.10，9.29，9.78，9.29，10.47，11.46，8.73，10.10，9.29，11.46，8.86，10.93，9.78，9.29，10.47，9.29，11.92，10.47，8.86，10.10，9.78，9.16，10.93，10.93，9.16，11.92，10.93，11.12，10.10，10.10，9.29，9.78]。序列弱化效果对比如图2所示。

步骤 4：计算置信区间与灰度。采用式⑻计算序列 XN的均值 μ 在置信水平 0.95 (α取 0.05) 下的置信区间为 [9.88,10.47]，代入式⑺得出灰度 g0＝0.04<0.15，达到精确度要求。由此，可得出渡口方向接到达货物列车时间标准 t接货＝[9.88，10.47]0.04。

同理，可计算出：t发货＝[7.69，8.62]0.06，t接单＝[5.52，6.54]0.10，t发单＝[3.48，4.56]0.13。

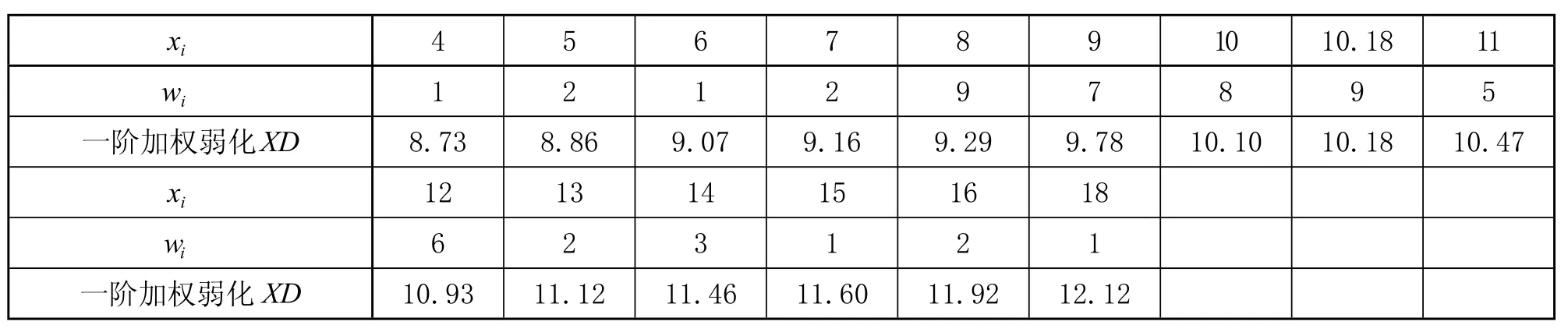
表1 加权弱化计算表

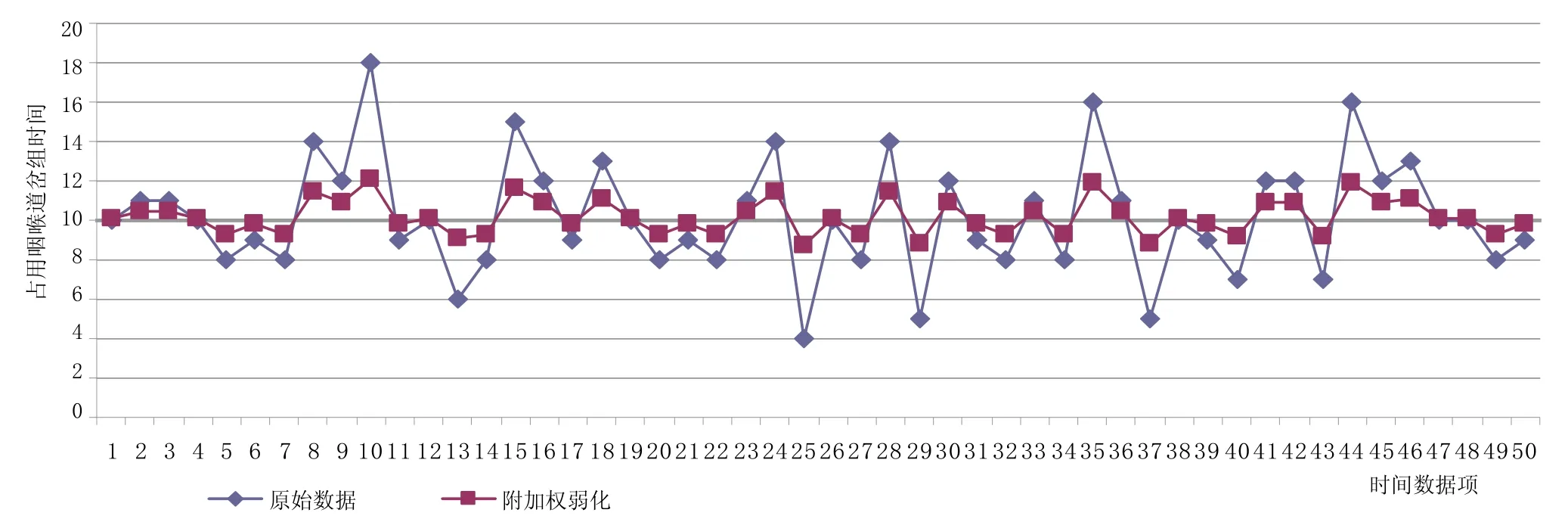
图2 序列弱化效果对比图

步骤 5：代入式⑼计算渡口方向咽喉区各道岔组的总占用时间 T。渡口方向咽喉区道岔组共3 组，分别为 2、4、6 号道岔组。2 号道岔组3个昼夜总占用时间为：

同理计算得出4号道岔组总占用时间T4＝[1 957.46，2 014.30]0.13，6 号道岔组总占用时间 T6＝0。

采用式⑽计算得到可能度矩阵为：

由可能度矩阵可知，n1＝2，n2＝1，n3＝0，则可得排序结果为 T2＞T4＞T6，因此，2 号道岔组为负荷量最大的道岔组 (即咽喉道岔组)。

步骤 6：将2号道岔组总占用时间 T2代入式⑾计算2号咽喉道岔组的利用率：

按铁道部能力表示标准表格[9]统计，渡口方向3个昼夜接发列车的实际数量如表2所示。

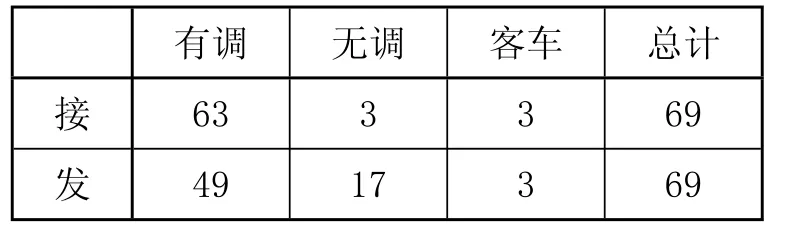
表2 渡口方向接发列车实际数量列

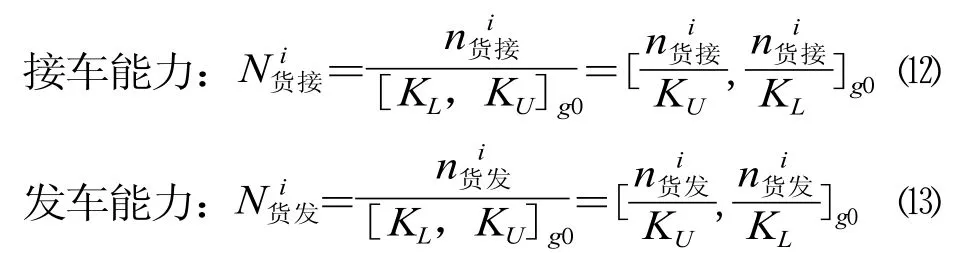
将 K 和表2数据代入式⑿、⒀，计算2号咽喉道岔组的通过能力 (即为渡口方向咽喉道岔组通过能力)，其计算结果如表3所示。传统方法的计算结果如表4所示。

表3和表4比较可知，传统方法计算结果包含在本文方法计算结果的区间内，同时结合灰度表明区间估计的精确度，有效弱化了干扰因素对时间数据造成的波动，计算结果具有良好的可靠性与精确度。

表3 本文方法计算结果列

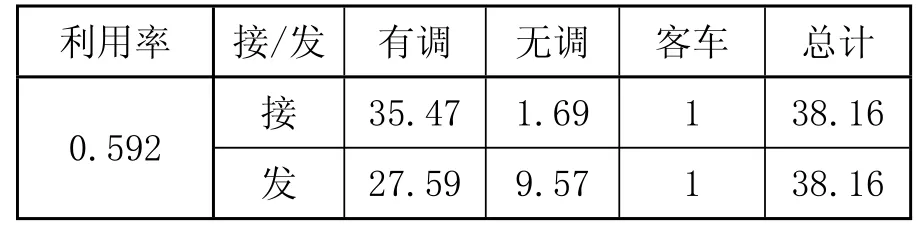
表4 传统方法计算结果列

5 结束语

在实际的车站能力查定过程中，由于各种随机因素的干扰，原始数据通常呈现出较大的波动起伏。对原始数据序列的弱化处理可有效地减轻或消除干扰因素的影响，使时间标准的变动更趋于稳定。在此基础上进行时间标准的区间估计，使时间标准的确定更为科学。与以往的能力计算方法相比，引入灰度这一概念来表征区间估计的精确性，使计算结果兼顾了可靠性与精确性。该计算方法可推广应用于到发线通过能力及改编能力的计算。

[1]孔庆钤，刘其斌. 铁路运输能力计算与加强[M]. 北京：中国铁道出版社，1996.

[2]刘 旭，谭立刚，杨 浩，等．编组站通过能力和改编能力模拟计算系统的研究[J]．铁道学报，2002，24(5)：11-15.

[3]李海鹰，张 超．编组站到解系统通过能力计算方法[J]．中国铁道科学，2010，31(3)：120-125.

[4]李映红，唐优华，王慈光．技术站通过能力查定方法及数据处理系统的研究[J]．铁道运输与经济，2003，25(8)：54-56.

[5]刘 澜，王 南，杜 文．车站咽喉通过能力网络优化模型及算法研究[J]．铁道学报，2002，24(6)：1-5.

[6]赵王梓.车站通过能力计算中的数据处理方法[J]. 中国铁道科学，2006，27(6)：113-116.

[7]刘思峰，党耀国，方志耕，等．灰色系统理论及其应用[M]. 5 版. 北京：科学出版社，2010.

[8]孙海龙，姚卫星. 区间数排序方法评述[J]. 系统工程学报，2010，25(3) ：304-312.

[9]曲星照. 站细编制与学习问答[M]. 北京：中国铁道出版社，2001.