高铁接触网感应电压的理论分析
2012-11-27王邠
王 邠
(南京铁道职业技术学院,副教授,高级工程师,江苏 南京 210015)
目前,复线电气化铁路建设发展很快,复线并行线路的感应电压导致人身伤亡的事故时有发生。以前,我国电气化铁道平均牵引电流200 A,但现在高铁动车牵引电流高达1 200 A,短路时达到12 000 A。当机车正常运行或接触网发生短路故障,感应电压增加几倍甚至十几倍时,容易造成人身伤亡的事故并对通信信号设备造成损坏。因此,分析电气化铁路感应电压产生的机理,研究感应电压的准确计算公式很有必要。对感应电压问题,现有参考文献多采用近似计算法[1],而且对感应电压进行简单的代数计算。实际上由于牵引电流高达1 200 A,简易计算法公式已经失效。另外感应电压是矢量,不能用简单的代数和计算。本文仅对复线并行线路的感应电压进行分析,利用电磁场的基本理论和方法,推导出电气化铁道感应电压的准确计算公式,正确评估高铁牵引网感应电压的影响,以便做好高速铁路的施工维护和设计工作。
1 感应电压的计算
牵引电流流过接触网时,将在接触网导线周围形成电场和磁场,对周围的环境有电磁影响。电磁影响分为电影响和磁影响[2]。磁影响是由于牵引电流沿接触导线通过时,在导线周围产生交变磁场。由于电磁感应的作用,在传输导线上产生感应电动势。电影响是由于接触网与传输线路之间存在电容,传输线路与大地之间存在耦合电容,接触网上的高电压就通过这2个电容入地形成回路,产生电流,并使传输线路上产生对地电压。
1.1 电影响感应电压的计算 电气化铁路结构,如图 1 所示[3]。
图1中的1为带电接触网导体,2为停电接触网导体,C12为1导体与2导体间等效电容,C11为1导体与大地间等效电容,C22为2导体与大地间等效电容。
根据电磁场的唯一性定理,即无论求解的过程如何,只要满足给定的边界条件,则求解的结果是一致的。那么,利用镜像法,将大地的影响等效为地下的一等值反向电流所产生的影响,其复镜象深度为h。电气化铁路结构等效结构,如图2所示。图2中h为接触网高度;d为轨道间距;a为接触网等效半径。
设导线1和2的单位长度带电量分别为±ρl。由于 a<<d,a<<h,可认为电荷均匀分布在表面上而可等效为2条位于其主线上的线电荷。地面的影响可用图2镜像电荷±ρl来代替,这样仍能保证地表面的电位为零。于是,地面上部空间任一点P的电位就等于这4条线电荷所产生的电位之和。
根据电位计算公式可得导线1表面P1点的电位为
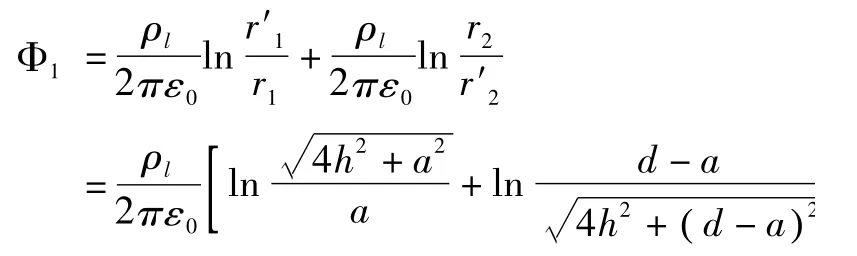
由于a<<d,a<<h,上式可近似为
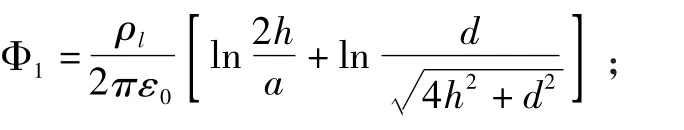
同理,导线2表面平p2点的电位近似为
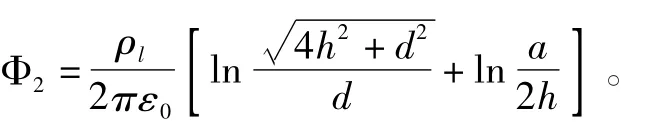
再求单位长度的 C11,C22和 C12。将导线 1、2单位长度带电量±ρl分别用 Q1,Q2表示,则
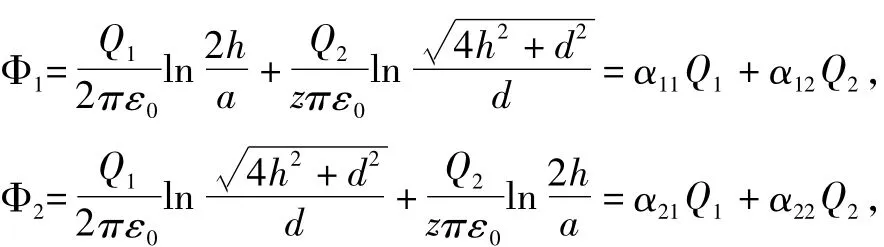
可求出导线1在导线2上的电容感应电位为
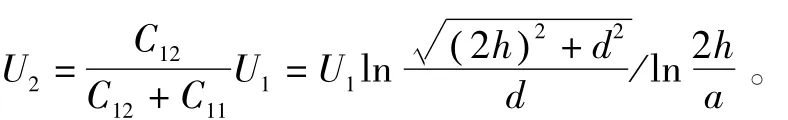
在具体计算的时候,相邻其他并行线路以及一些其它因素的影响,因此,计算的结果须乘以1个屏蔽系数。另外,由于C11和C12是单位长度的电容,计算出的电压也是接触网导线单位长度的电压,要得到接触网并行长度的电压还应乘以并行长度l。

图2 电气化铁路结构等效结构图
1.2 磁影响感应电压的计算 当带电接触网导线通过交流电流时,由于磁耦合作用,在邻近的停电接触网导体将产生感应电势,感应电势按下列公式决定,
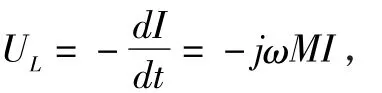
式中:M为互感;
I为接触网导线中的主扰电流。
由公式可知互感是一个非常重要的参数。
复线电气化铁路接触网等效结构,如图3所示。
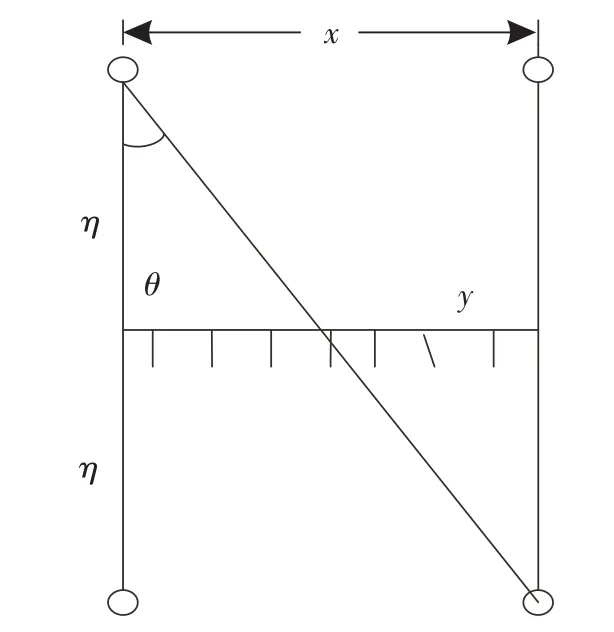
图3 复线电气化铁路接触网等效结构
其中,η=y=h是接触网等效高度,x=d是两接触网间的距离也是轨道间距。
由卡而生提出来的2单回线间的互感系数公式
M=M0-j4J(p,q)10-7(H/m)。


而
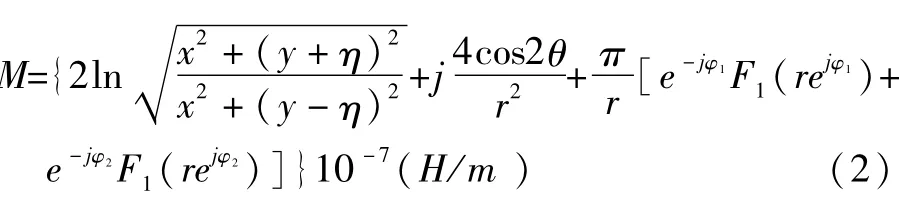
2 危险感应电压的计算
危险感应电压是指可能造成人身伤害的感应电压。国家标准GB6830—86对危险纵电动势的规定是不超过人体安全电压(6OV)。在接触网产生短路情况下,导线中感应出的纵电动势,不得超过其芯线绝缘电气强度的对地试验电压的60%。
2.1 计算公式 设牵引网功率角为ϕ,电容耦合感应电压为Uc=U2,电感耦合感应电压为UL,由于电容和互感耦合感应电压并非同相位,应计算其矢量和。根据交流电计算方法,总的感应电压为
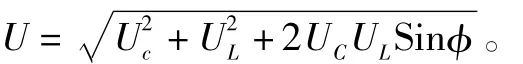
2.2 计算实例分析 复线电气化铁道的轨道间距5 m,带电线路功率因数为0.8,并行长度1 km,接触网等效高度6m,接触网等效半径为8.56mm,σ大地导电率为0.25×10-3Ω/m,静电综合屏蔽系数为0.8,牵引电流1 000 A。
计算出电容耦合感应电压Uc=U2为

电感耦合感应电压UL求得
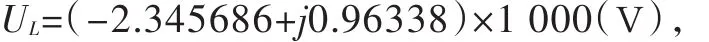
取其模值为|UL|=2.539(KV),
进而求出总感应电压为

计算结果危险感应电压数值很大,必须做好防护措施,否则可能造成人身伤亡和设备损毁事故。
3 结束语
在复线并行电气化铁道线路中,当带电接触网导线通过交流牵引电流时,接触网导线周围形成电场和磁场,对邻近的停电接触网导体产生电磁影响,电影响感应电压与带电线路电压成正比,磁影响感应电压与牵引电流的大小及并行长度成正比,总的感应电压是电容和电感耦合感应电压的矢量和。
在高速铁路中,牵引电流高达1 200 A,短路时达到12 000 A,危险感应电压计算必须采用精确的计算方法。高速铁路机车正常运行或接触网发生短路故障时,感应电压将增加几倍甚至十几倍,危险感应电压数值很高。由于高铁牵引电流高达1 200A,简易近似计算法公式已经失效,如果采用以前的简易近似计算法公式,引起计算错误,对施工维护工作及周围电子设备的防护工作造成损失。因此,正确评估高铁牵引网感应电压的影响,对做好高速铁路的施工维护和设计工作非常重要。
[1]王杰文.基于两线一轨制的感应电压计算[J].高电压技术,2005(6):22-24.
[2]王邠.交流电气化铁道通信电磁防护的研究[J].铁道工程学报,2007(3):60-64.
[3]冯慈璋.电磁场[M].北京:高等教育出版社,1990.
[4]高攸纲.电磁兼容总论[M].北京:北京邮电大学出版社,2005.
