ANP_FE技术在地铁隧道近接施工风险评估中的应用

2012-11-27郑余朝李俊松

铁道标准设计 2012年12期

李辉，郑余朝，李俊松

(1.西南交通大学交通隧道工程教育部重点实验室，成都 610031;2.中国中铁二院工程集团有限责任公司，成都 610031)

地铁作为缓解和改善城市地面交通拥堵情况的主要交通工具，开始得到前所未有的关注和重视。预计在2015年前后，我国将建设79条以地铁为主的轨道交通线路，总长约2 260 km，总投资近9 000亿元。由于地铁主要建设在城市中心地带，故不可避免地存在形形色色的地铁隧道施工近接情况［1］。

地铁隧道近接施工过程具有不确定性和模糊性影响因素多、施工工序复杂、安全控制标准高、社会影响巨大等特点，因此地铁隧道近接施工是一类高风险的工程项目［2］。如何对地铁隧道近接施工风险进行评价、控制和管理，确保周围建(构)筑物的安全，是广大学者和科研工作者面临的急需研究和亟待解决的一个问题。尽管风险管理引进隧道施工中已有50余年，但对地铁隧道近接施工风险的研究甚少，主要对近接施工风险发生机制、机理及风险保证体系进行了研究，如黄宏伟［3］对城市隧道施工的复杂近接环境进行了分类，并得到了软土地层中盾构隧道近接施工风险发生机理图。骆建军［4］等基于近接地面建筑物的沉降控制标准，结合施工中的监控量测，对近接风险进行了控制。侯艳娟［5］等通过对城市隧道下穿建筑物施工，监控量测，方案优化等几个方面研究和分析，建立了能够指导实际近接施工的安全风险管理体系。由此可见，地铁隧道近接施工风险研究还停留在定性分析阶段，缺乏有效的定量风险评估方法，难以实现对风险的控制和管理。

现阶段常用的半定量或者定量的风险评价方法有层次分析法(AHP)、网络层次分析法(ANP)、模糊综合评价法(FE)、神经网络法等。其中，由于ANP［6］能够解决事物影响因素之间存在相互依存和反馈情况的风险评价问题，而逐渐被人们重视和推广。而FE［7］能够对具有模糊性质的事物做出很好的评价。本文针对目前地铁隧道近接施工风险研究中存在的问题，在已有研究成果的基础上，综合考虑到隧道近接施工风险影响因素具有相互依存、反馈和模糊性等特点，最终选择将ANP与FE结合起来构成ANP_FE作为主要的风险评价方法。通过ANP的运用求得底层因素的整体权重向量，再结合FE计算出地铁隧道近接施工的风险度，然后根据风险评价结果制定风险应对措施，最终实现了风险的定量控制和管理。最后，结合广州地铁某隧道的近接施工工程说明了该法的具体实施过程，确保了施工的顺利进行和周围结构物的安全。

1 地铁隧道近接施工风险评价指标体系

地铁隧道近接施工中风险影响因素繁多，且各因素之间存在相互依存和反馈关系。通过对国内地铁隧道近接施工工程的调查和现有资料的研究分析，得到了地铁隧道近接施工风险的主要控制因素有安全性、技术性、经济性和环境效应;其主要影响因素(元素组)有地质情况、近接情况、设计、施工和安全控制标准等;然后对元素组进行分解和归类，即可得到21个底层因素，具体情况见表1。

表1 地铁隧道近接施工风险评价指标体系

地铁隧道近接施工风险指标体系不再是单纯的递阶层次结构［8］，不仅元素组之间存在相互依存和反馈，而且各元素组下各因素之间也存在此关系，最终形成了由控制因素层和网络层［9］组成的复杂网络层次结构，如图1所示。

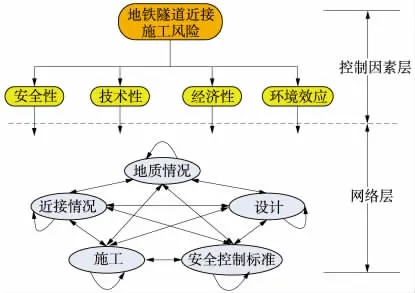
图1 地铁隧道近接施工风险网络层次结构

2 风险评估与管理基本理论

2.1 ANP_FE风险管理理念介绍

运用网络层次分析法(ANP)的相关理论和算法［10］求得针对于所有底层因素的整体权重向量。再凭借专家打分和隶属向量的结合得到底层因素的模糊综合评价矩阵。然后利用模糊集合变换原理计算得到地铁隧道近接施工风险的风险等级，并查找出对风险评价目标影响较大的那些因素，采取针对性较强的措施对风险进行控制和管理。

2.2 ANP理论

由于层次分析法(AHP)［11］只能解决那些要求同层元素相互独立，且只能上层支配下层的递阶层次结构模型问题，于是在1996年，Saaty［6］教授通过对AHP的总结和提炼，提出一种适宜解决各元素之间存在相互依存和反馈的复杂网络结构模型的方法——ANP。

(1)计算权重向量，合成超矩阵和加权矩阵。

由于网络层次结构模型中各元素之间并不相互独立，而是存在相互依存与反馈关系。因而需要利用1－9比例标度法，以Ti为准则，以Tij为次准则，对Tk下各因素进行间接优势度比较。通过比较得到判断矩阵B，然后运用根法求得各判断矩阵对应的特征向量=(w1，w2，…，wn)T，(i，j，k=1，2，…，n)，计算式如下

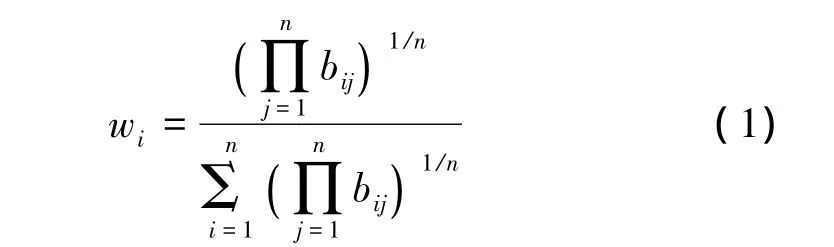
式中，bij为位于判断矩阵中第i行第j列的元素，是bi与 bj的重要性比较结果，并且存在关系bij=1/bji。

将所有的特征向量进行合成，便可构成超矩阵。对于元素组，采用和上述相同的计算方式可以求得加权矩阵K。

(2)求解加权超矩阵，得到底层因素对应的整体权重向量。

由上面得到的超矩阵和加权矩阵，通过加权运算，便可求得加权超矩阵。考虑到求解精度的要求，本文采用特征向量法对加权超矩阵进行求解。首先由式(2)求得加权超矩阵模最大的特征根λmax。

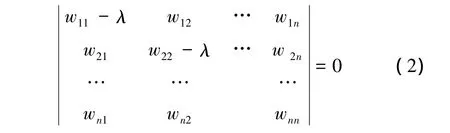
然后利用式(3)计算出最大特征根对应的特征向量w，归一化处理之后即为底层因素的整体权重向量。

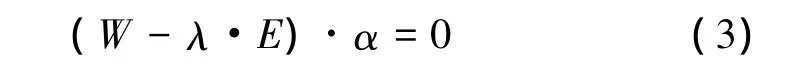
式中，E为单位矩阵;λ为矩阵W的特征根;α为特征根λ对应的特征向量。

2.3 FE理论

模糊综合评判方法(FE)是基于模糊数学理论，由L.A.Zadeh［7］教授于 1965 年提出的针对于事物影响因素多，且因素不确定性和模糊性较强的一种评价方法，其关键在于模糊综合评价矩阵的运算。通过评语集的建立，将定性评价转换为定量评价，构成模糊评价矩阵。结合上文中求得的权重向量，选择合适的模糊算子进行计算，最终可得到事物的评价结果。

(1)评语集的建立

评语集是由针对评价对象的所有评价结果所组成的集合，评语集的级数需根据评价对象的复杂程度而定，一般取为4 到6 级，即 V=(V1，V2，…，Vn)T，(4≤n≤6)。

(2)模糊综合评价矩阵的建立

利用专家调查法求得各底层因素的评价结果。根据评语集，对评价结果进行统计分析，可以计算得到各底层因素的隶属向量。最后综合合成所有隶属向量，便可得到模糊综合评价矩阵。

(3)模糊评价

模糊算子的选择有多种，这里选用“乘与和模糊算子”构成模糊综合评价模型

式中，P为评价对象的隶属向量;w为权重向量;R为模糊综合评价矩阵。

最终的评价结果可以根据式(5)求得

3 案例分析

本文以广州地铁某隧道近接施工工程为例，说明了该风险管理理念和方法的具体实施过程。

3.1 工程概况

广州地铁6号线某区段地层与周围水系相连，地下水较丰富;岩层自上而下40 m范围内依次为杂填土、淤泥质土、粉质细砂、粉质黏土、中风化砂岩层。隧道拱顶埋深在25～30 m，隧道主要从中风化砂岩层中穿过。根据设计方案，该区段隧道涉及盾构法和矿山法两种施工方法;且存在单线小断面和双线、三线大断面等多种断面形式，隧道最大净跨为19.6 m。

本区段的规划设计中存在多类隧道工程近接情况，既包含间距仅为11 m的两暗挖隧道自身在先后施工过程中的近接，又存在大断面隧道与仓库A1、车间及住宅楼A2的近接(图2)，其中隧道拱顶与A1桩基间的最小距离仅为1.7 m。因此，无论从工程近接复杂程度还是综合施工难度方面考虑，都存在较高的工程风险。

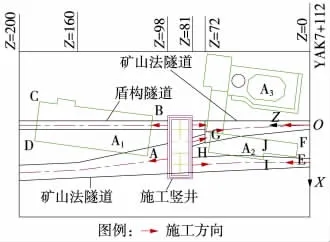
图2 隧道近接关系平面示意(单位:m)

3.2 ANP计算权重

超矩阵都是在考虑元素组之间各元素的相互关联性之后，在准则Ti与次准则Tij下通过间接优势度比较后得到各比较判断矩阵，进而求得特征向量，然后由特征向量综合合成得到的。如以T3为准则，T31为次准则，对元素组T1中各元素作两两比较，得到判断矩阵，然后利用式(1)求得其特征向量

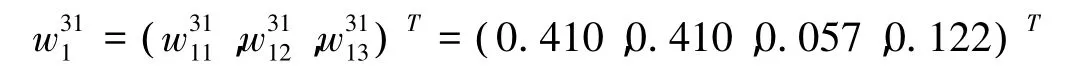
同理可得w321，w331，w341，w351，便可合成子矩阵

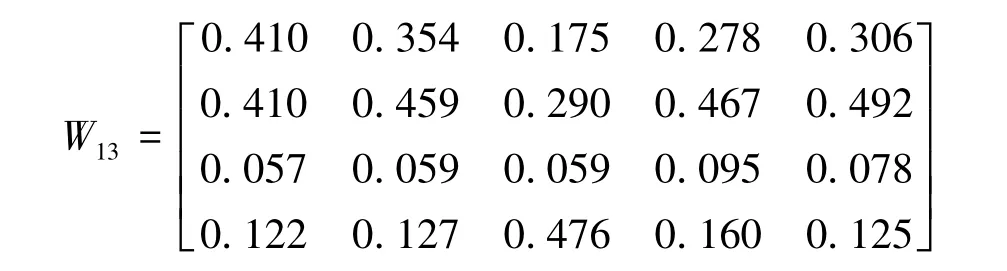
重复上面的步骤，可计算得到其余24个子矩阵W11，W12，W14，W15，W21，W22，…，W55，最终合成超矩阵

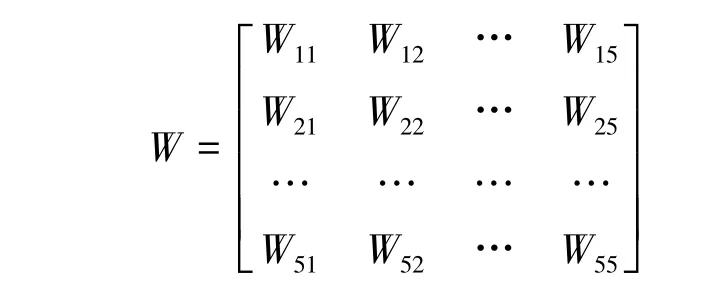
同样，利用间接优势度对各元素组进行两两比较，求得特征向量后便可合成加权矩阵

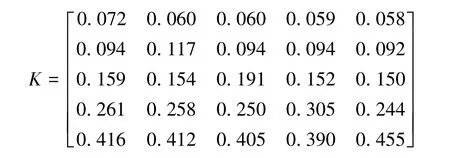
然后利用加权矩阵对超矩阵做加权，即得加权超矩阵¯W。最后根据式(2)计算得到加权超矩阵模最大的特征根λmax=1。再将其代入式(3)求得特征向量w，归一化处理后即为底层因素的整体权重向量，各权重值如表2所示。

3.3 FE计算风险

评语集是模糊综合评价法的基础，是定性评价向定量评价转换的关键。考虑到该工程的实际情况，将评语集设定为4 级，即 V=(4，3，2，1)T，分别代表(风险高，风险较高，风险一般，风险小)。

然后邀请20个对相关工程比较熟悉的技术人员、科研工作者、学者组成专家组，对所有底层因素打分，求得各底层因素针对于评语集的隶属向量。再将所有隶属向量综合合成，即可构成模糊综合评价矩阵(表2)。

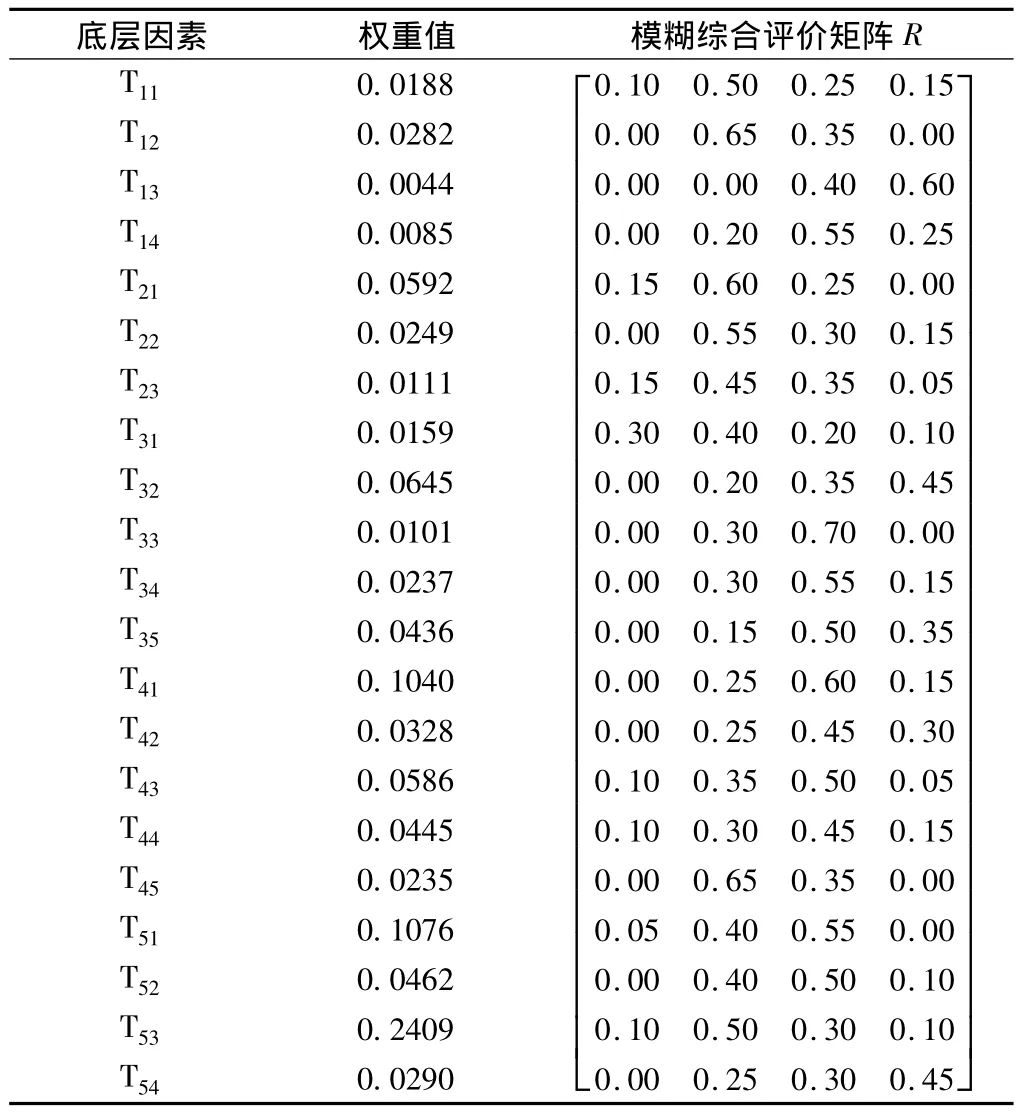
表2 底层因素的权重值及模糊综合评价矩阵

根据表2，将权重向量和模糊综合评价矩阵的具体值代入式(4)，计算得到地铁隧道近接施工风险的隶属向量

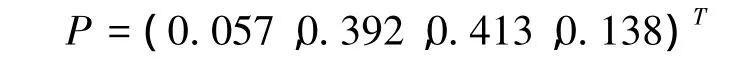
最后可根据式(5)求得地铁隧道近接施工的评分S=2.368∈［2，3］。由评语集可知，地铁隧道近接施工风险较高，需采取有效措施对风险进行控制和管理。

3.4 风险应对措施

由底层因素的整体权重向量可知，对地铁隧道近接施工风险影响最大的前4个因素依次为建筑物沉降及倾斜度、地表沉降、施工工艺合理性、支护设计。而从模糊综合评价矩阵中可以看出隧道高跨比、近接距离、岩体完整性、施工安全管理也会给工程带来较高的风险。其中主要风险为由于隧道开挖引起建筑物沉降及倾斜度过大而造成周围建筑物开裂、破坏甚至坍塌。为了有效地规避和降低施工风险，决定选择采取以下措施对风险实施控制和管理:

(1)以管棚和超前小导管预注浆作为主要超前支护手段［12］，改善和提高隧道周边的围岩稳定性。在大跨断面隧道拱顶150°范围内沿开挖轮廓线平行设置φ89 mm，厚5 mm，长8 m的短管棚;在一般断面处采用φ42 mm，厚3.5 mm，长3 m的超前小导管，以15°外插角，沿隧道拱顶120°范围内打入岩层并注浆;同时对建筑物周围地表实施预注浆处理;

(2)矿山法施工隧道以钢筋网、锚杆、格栅钢架作为主要的围岩支护体系，在多线交汇的大跨断面处，采用双侧壁导坑法施工;一般断面则采用CRD法施工;

(3)对隧道上方的人流和车流进行疏导与控制，减少施工隧道的地面载荷。