非正常航班管理中的飞机恢复问题研究

詹晨旭，乐美龙

（上海海事大学物流研究中心，上海 200135）

中国民航局发布的民航行业发展统计公报披露，2010年，中国国内大型航空公司计划航班188.8万次。其中，正常航班143.1万次，不正常航班45.7万次，航班不正常率为24.2%。2010年，中国中小航空公司计划航班26.0万次。其中，正常航班17.9万次，不正常航班8.1万次，航班不正常率31.2%。根据民航局披露的数据，2010年，在导致主要航空公司航班不正常的原因中，航空公司自身原因占到41.1%；流量控制占27.6%；天气占19.5%，其他占到11.8%。在对中小航空公司航班不正常原因进行的统计中，航空公司自身原因高达47.9%。

无论是由于飞机故障、机组人员病假等航空公司的原因，还是天气、流量控制等其他原因，航班不正常难以避免。在发生航班不正常时，采用科学的方法，尽快恢复航班尤其重要。

目前的航空恢复研究主要关注飞机资源，这是因为飞机资源是航空公司最为重要的资源（Kohl et al.2007）[1]。

Teodorovic 和 Guberinic（1984）[2]是最早研究飞机恢复问题的学者之一。他们从运营的角度研究这一问题，考虑当出现某一架飞机无法执行任务的情况时，通过交换航段和延误航班达到最小化乘客延误的目的。他们构建了一个数学模型，并通过分支定界法求解该模型。但是许多实际运营中的约束条件，例如机场宵禁、飞机维护约束和飞机平衡约束等在他们的模型中并未体现。此外，航班取消这一选项也未被考虑。而 Clarke（1998）[3]，Filar et al.（2001）[4]，Andersson 和Varbrand（2004）[5]，Kohl et al.（2007）[1]，Yu and Qi（2005）[6]以及 Clausen et al.（2010）[7]等对飞机恢复问题的概念与模型均提出了综合性的回顾。Yan S.and Yang D.（1996）[8]提出了一个包含航班取消、航班延误和调用飞机等选项的模型，以解决飞机恢复问题。他们的模型基于若干假设：单一机队；所有的航班都是不经停航班；仅有1架飞机出现无法执行航班状况。同时，他们还提出了一个时空网络用以表述飞机恢复问题，该网络满足前述的3个选项。该模型的目标函数是最小化航班时刻表受干扰时间。通过利用中华航空的实际数据，运用拉格朗日松弛方法，对模型进行了检验。

Jay M.Rosenberger，Ellis L.Johnson，George L.Nemhauser（2003）[9]将飞机恢复问题转化为一个带时间窗约束和时间槽约束的集覆盖（setpacking）问题。在他们的模型中，目标函数是最小化总成本，包含飞机重新指派路径成本和航班取消成本。Teodorovic和Sto jkovic（1990）[10]提出了一个启发式算法用来解决飞机恢复问题。在他们的文章中，最小化取消航班数量与乘客延误总数是目标函数，但是没有考虑航班延误成本以及取消成本。Michael F.Arguello，Jonathan F.Bard，Gang Yu（1997）[11]提出了一个基于随机临近搜索的启发式算法用以解决飞机恢复问题。在文章中，他们创造了一个贪婪随机适应搜索程序（GRSAP），用这一程序重建飞机路径以应对干扰。目标函数是最小化飞机路径指派成本和航班取消成本。但是在他们的程序与模型中并没有考虑飞机维护要求和机组限制。Jonathan F.Bard，Gang Yu和 Michael F.Arguello（2001）[12]也对飞机恢复问题提出了一个时间带优化模型。通过将飞机路径问题转化为一个基于时间的网络，他们构建了时间带模型，并将飞机恢复问题视作一个最小成本流问题。Thengvall B.，Bard J.，Yu G.（2000）[13]对 Michael F.Arguello，Jonathan F.Bard，Gang Yu（1997）[11]的网络模型进行了拓展。他们所提出的模型中，目标函数中使用了偏离原时刻表罚值，并以其最小化为目标。同时，其允许人工计划员指定与恢复操作相关的参数。测试数据包括2个机队的27架飞机。Eggenberg N.，Bierlaire M.，Salani M.（2007）[14]提出了一个扩展的时空网络模型，目标函数是最小化包括航班延误、取消成本，飞机航段交换成本以及完成成本（makespan cost）在内的总成本。

本文以飞机恢复为主要研究内容，提出一个飞机恢复的优化模型，并给出一个解决飞机恢复问题的启发式算法。第1章阐述恢复模型；第2章介绍启发式算法；在第3章中，若干算例将被应用，利用算例对模型和算法进行了验证分析；最后，第4章对模型及算法进行了总结，并提出了后续研究改进的方向。

1 飞机恢复模型

依照航空公司的日常运营，考虑所关注的飞机资源，本文为某一时间周期内的飞机恢复问题建立了模型。在建立模型时，考虑到飞机恢复的最终目标是恢复航班时刻表，因而本文引入原始时刻表和修正时刻表两个概念。原始时刻表是指在干扰情况发生之前，航空公司所计划执行的时刻表；修正时刻表是指产生干扰后，经过恢复操作所得到的时刻表。本文将机场分为两类，一类是可执行飞机维护操作的机场，剩余的机场归为一类。具体参数、变量如下：

T=[t，t]为时间周期；OS为原时刻表；RS为修正的时刻表；F为航班集合；A为机场集合；AC为飞机集合；H为需要在T内维护的飞机集合；Amaint为可以执行飞机的计划维护的机场集合；TF为原时刻表中的航班总数（）为在时刻和时刻之间机场 a的到达容量（ta，ta）为在时刻和时刻之间机场a的离开容量（）为在和之间进入机场 a的航班集合；F-a（ta，ta）为在 ta和 ta之间离开机场 a 的航班集合为将航班f∈F指派给修正时刻表RS的成本为航班f∈F的取消成本为航班f∈F的每分钟延误成本为航班f∈F上乘客的每分钟延误成本为将飞机n∈AC指派给航班f∈F的成本为飞机n∈AC上每个座位空闲的成本；sea（tn）为飞机n∈AC上的座位数量；CAP（f）为航班f∈F要求的座位数；taf为航班f∈F的实际到达时间；Tf为航班f∈F的计划到达时间；tdf为航班f∈F的实际离开时间；DTf为航班f∈F的飞行时间；TurnTime（n）为飞机 n∈AC 的转向（turnaround）时间；xf为1，如果航班f∈F被指派给修正时刻表RS；lm，n为1，如果一个合格的维护机场m∈Amaint被飞机n∈AC 访问；yn，f为 1，如果飞机 n∈AC 被指派给航班f∈F；zf′，f为 1，如果航班 f′是航班 f的后接航班。

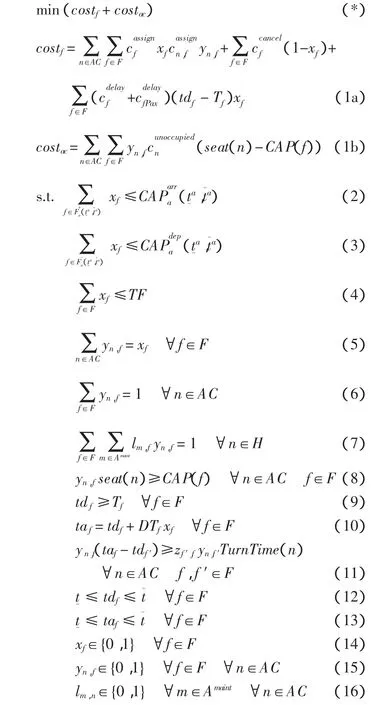
式（*）是总成本目标，即最小化航班成本与飞机成本。

式（1a）中，第1项是指派成本，即将航班f指派给修正时刻表RS，且由飞机n执行航班f的成本；第2项是航班取消成本；第3项是航班延误成本，与延误时间有关。延误成本既包括航班自身延误产生的成本，也包括该航班上乘客的延误成本。式（1b）是因座位空闲而造成的成本。

约束条件中，式（2）指在时段T内，进入机场a的航班数量受机场到达容量的限制。式（3）指在时段T内，离开机场a的航班数量受机场离开容量的限制。航班数量约束，即被指派的航班数量不超过总航班数，在式（4）中体现。式（5）约束航班指派，即航班指派给飞机时的0-1约束。飞机指派约束在式（6）中限制，每架飞机只能被指派1次。式（7）体现飞机维护约束，需维护的飞机要求访问有维修资格的机场。航班容量约束在式（8）中体现，如果飞机n被指派给航班f，则飞机上的座位数应不小于航班要求的座位数。式（9）～式（13）约束航班时间。式（9）约束离开时间，即航班f的实际离开时间应不小于其计划离开时间。式（10）约束到达时间，即航班f的实际到达时间等于其实际离开时间加上飞行时间。式（11）体现飞机转向（turnaround）时间约束，即如果航班f′是航班f的紧接航班，若它们由1架飞机执行，则这两个航班间的到达和离开时间差应大于该飞机的turnaround时间。式（12）、式（13）表明实际离开时间和实际到达时间应在时间范围T内。式（14）～式（16）是0、1变量约束。

2 解决方法

本文设计了一种基于改进的随机搜索策略的启发式算法，该算法主要参考GA算法思路。通过迭代计算，得到每次迭代结果较优的可行解，并在迭代中对解搜索方向加以引导，逐次逼近最优解，提高搜索精度，加快搜索速度。参考GA求解思路，首先定义可行解空间容量为M，该空间里的可行解是迭代的对象；然后对每次迭代得到的可行解按照成本最小（目标函数要求）排序，并保留前Mα个可行解，将其直接作为下次迭代的结果；再对可行解进行迭代，直至迭代次数达到之前所设定的值。算法流程如图1所示。具体算法步骤如下：

步骤1 按照FCFS（先来先服务）策略延误或取消OS中受干扰航班，得到M个初始RS，若调整受干扰航班无法得到M个初始解，则复制任意一个初始解，填充剩余初始解空间，将所有初始解记为RS01，…，RS0m。

步骤2 对RS0*按成本升序排列，保留前Mα个RS0*，将其视作本次调整所得的结果，并调整剩余的M（1-α）个RS0*。随机挑选一个剩余RS0g，调整其解结构（即调整其航班属性——到达时间或离开时间，以及执行飞机），得到一个新RS，如果新RS的成本不比调整前的RS0*成本大，则将其保留，并记为RS1*。

步骤3 对RS1*重复步骤2，得到RS2*。

步骤4 重复步骤2与步骤3，直至完成之前设定的迭代次数，得到RSn*。

步骤5 按成本，升序排列RSn*，将RSn*中成本最小的解作为解决方案，并输出。

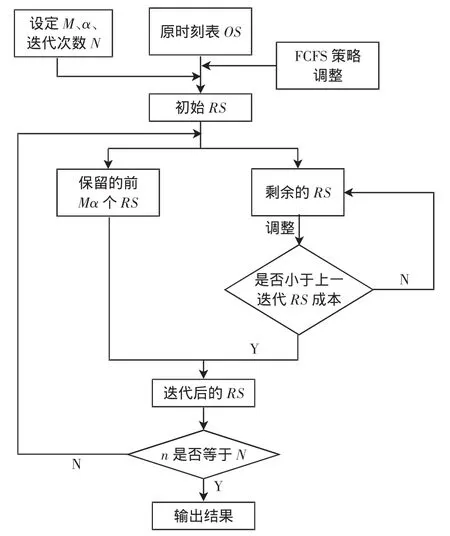
图1 算法流程Fig.1 Algorithm process

3 算例与结果分析

3.1 算例

本文使用国内一家航空公司的实际数据来测试模型与算法的有效性。该航空公司主要运营国内航班，以PVG与SZX为其运营基地，在NKG、PVG、SZX、PEK、XIY等5个机场具备飞机维护资格。该航空公司一个周期内的航班时刻表包含198个航班，由32架飞机执行，飞机机型计有5种，包括B747、B777、A300、A310以及A320。本文所用数据节选自该航班时刻表，基本数据汇总如表1所示，飞机具体数据如表2所示。

表1 基本情况Tab.1 Basic information

表2 机型数量Tab.2 Aircraft type and number

由于该航空公司以国内航班为主，因而其航班基本上为短途航班，即飞行时间在3 h以下。将时间窗设定为 T=[t，t]=[07：00，24：00]，设=0元=25 000元=50 元/min=50 元/min如表2所示为每个航班上的座位票价。在求解时，设可行解空间容量M=50，解保留比率α=10%，迭代次数N=5 000。

对于干扰情况，由于在模型中较为关注机场某时段的容量变化，因而本文将干扰情况设定为：某日因天气状况，PVG 机场在 12：00关闭，直至 13：30，即在12∶00～13∶30内，PVG 容量减为 0。

3.2 结果分析

使用C#语言实现启发式算法，在CPU为CORE i3 2.13 GHz，内存为2 GB的PC上运行该算法，求解问题。针对前述的干扰情况，按照不同的迭代次数，得到不同的解决方案。可以发现，随着迭代次数的增加，成本越来越趋近于某一值。在迭代5 000次之后，发现成本值曲线接近平缓，得到的成本值为28 587.45元。迭代次数与成本值之间的关系如图2所示。而使用LINGO 9.0求解该问题，最优解为28 314.10元。使用启发式算法得到的最终解，较最优解高0.97%。因此，认为该最终解可被接受，可被视作最终解决方案。

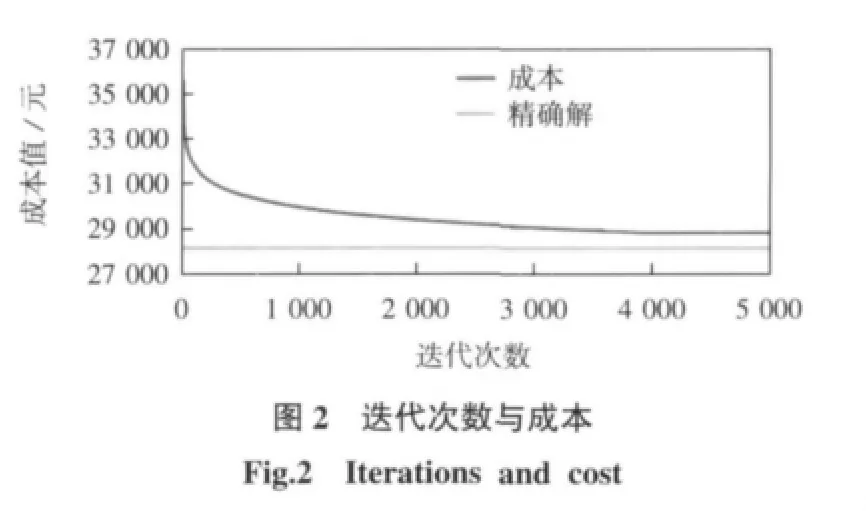
在最终解决方案中，取消航班数为0，延误航班数为13班次，占总航班的21.67%，产生的总成本为28 587.45元。而按照迭代次数的不同，产生不同的解决方案，各方案航班信息如表3所示。

表3 各方案航班信息Tab.3 Flight information of each solution

启发式算法得到的最终解决方案产生28 587.45元的总成本，较按FCFS策略延误航班产生的成本（35 569.95元）减少19.63%，所花费的求解时间为19 min，较精确解求解所花时间（42 min）减少54.76%。

4 结语

本文所提出的模型主要针对于航空公司非正常航班管理中的飞机恢复问题。当受到干扰时，可以辅助管制员实施调度。在尽量恢复原计划的同时，其延误率也大大降低。由于该模型所涉及到的数据量较多，因此该模型适用于中小型航空公司。

对于所设计的启发式算法，使用了不同规模的数据进行了测试。在较小规模数据（3架飞机、18个航班、12个机场）情况下，算法表现良好，迭代5 000次，花费8 min得到结果；中型数据（13架飞机、60个航班、25个机场）情况下，迭代5 000次，花费19 min得到结果；而对于大规模数据（25架飞机、154个航班、46个机场）情况下，迭代5 000次，花费51 min。可以看出，随着数据规模的扩大，本文所设计的启发式算法的搜索效率则大为下降，因而可考虑使用其他效率较高的启发式算法。

需要指出的是，本文所提出的模型属于非线性，因此，其结果为局部最优解。本文最大的约束在于不允许产生新的航班，但是在实际活动中产生的干扰情况是多种多样的。因此，针对不同的情况，应该建立一个适应度更强的模型。针对本文所提出的方案也可有多方面的拓展。

[1]KOHL N，LARSEN A，LARSEN J，et al.Airline disruption management perspectives，experiences and outlook[J].Journal of Air Transport Management，2007，13：149-162.

[2]TEODORVIC D，GUBERNIC S.Optimal dispatching strategy on and airline network after a schedule perturbation[J].European Journal of Operations Research，1984，15：178-182.

[3]CLARKE M D D.Irregular airline operations：a review of the state-ofthe-practice in airline operations control centers[J].Journal of Air Transport Management，1998，4：67-76.

[4]FILAR J A，MANYEM P，WHITE K.How airlines and airports recover from schedule perturbations：a survey[J].Annals of Operations Research，2001，108：315-333.

[5]ANDERSSON T，VARBRAND P.The flight perturbation problem[J].Transportation Planning and Technology，2004，27：91-117.

[6]YU G，QI X.Disruption Mmanagement：Frameworks，Models and Applications[M].Singapore：World Scientific Publishing，2004.

[7]JENS CLAUSEN，ALLAN LARSEN，JESPER LARSENA，et al.Disruption management in the airline industry——concepts，models and methods[J].Computers & Operations Research，2010，37：809-821.

[8]YAN S，YANG D.A decision support framework for handling schedule perturbations[J].Transportation Research，1996，30（6）：405-419.

[9]JAY M ROSENBERGER，ELLIS L JOHNSON，GEORGE L NEMHAUSER.Rerouting aircraft for airline recovery[J].Transportation Science，2003，37（4）：408-421.

[10]TEODOROVIC D，STOJKOVIC G.Model for operational daily airline scheduling[J].Transportation Planning and Technology，1990，14：273-285.

[11]MICHAEL F ARGUELLO，JONATHAN F BARD，GANG YU.A GRASP for aircraft routing in response to groundings and delays[J].Journal of Combinatorial Optimization，1997，5：211-228.

[12]JONATHAN F BARD，YU GANG，MICHAEL F ARGUELLO.Optimizing aircraft routings in response to groundings and delays[J].IIE Transactions，2001，33：931-947.

[13]THENGVALL B，BARD J，Yu G.Balancing user preferences for aircraft schedule recovery during irregular operations[J].IIE Transactions，2000，32：181-193.

[14]EGGENBERG N，BIERLAIRE M，SALANI M.A Column Generation Algorithm for Disrupted Airline Schedules[R].2007.