五轴联动数控加工的装夹误差动态补偿方法*

赵 鹏，楼佩煌，刘明灯，满增光

(1.南京航空航天大学机电学院，南京 210016;2.南京四开电子企业有限公司，南京 210007）

0 引言

现代航空，航天，模具工业中广泛采用精密五轴数控加工，其加工精度要求达到微米级别，传统工件装夹方式定位精度不高，无法满足精密加工要求。许多学者对装夹误差补偿方法进行了研究［1-4］。文献［1］研究了大直径环形件的装夹偏心补偿方法，文献［2］研究了专用机床的装夹误差补偿问题，文献［3，4］提出了工件装夹误差建模方法，对其进行离线预测补偿。这些研究没有对包含旋转轴的装夹误差情况进行分析，而五轴数控机床由于装夹误差引起实际旋转中心与CAM编程基准不一致，由此引起的附加运动无法通过常规的G54-G59方式补偿［5］，只能根据装夹位置调整编程基准重新进行CAM处理或者反复调整装夹精度，耗费大量时间。本文研究了五轴数控加工的装夹误差寻位补偿方法，动态修正加工路径，在保证加工精度条件下大大降低工件装夹难度，提高机床实际加工效率，具有广泛的工程应用意义。

1 五轴加工的工件装夹误差分析

在三轴数控加工中，装夹误差可以通过简单的坐标系偏置补偿，使编程基准与工件装夹位置一致。而五轴数控加工的NC代码中，旋转轴路径是根据CAM编程中的旋转中心位置决定的。由于装夹误差，编程旋转中心位置与实际机床旋转中心位置不一致，使得CAM生成的刀具路径发生偏移。如图1所示为一个典型的装夹误差状况，阴影部分表示CAM编程中设定的工件在机床上的位置，设定的旋转中心为机床实际旋转中心O，由于装夹偏差工件实际位置在图示实线所示部分，编程旋转中心位置偏移到点O'，旋转轴角度偏差为α。以工件上任意一点M为例，分析转动过程中由于旋转中心偏差造成的路径误差情况，如图2所示，工件装夹无误差时，点M随旋转轴运动路径为以机床旋转中心O为圆心的圆，如图中细虚线所示，和CAM编程路径一致;在装夹误差存在时，点M实际装夹位置为点M'，M'的理想运动路径应当是以O'为圆心的圆，如图中细实线所示，此时工件加工结果仍然与设计一致;然而由于机床运动中旋转轴是以机床旋转中心O为圆心的转动，点M'的实际路径是以机床旋转中心O为圆心的圆，如图中粗虚线所示，此时工件加工结果偏离设计形状;在旋转过程中，编程旋转中心O'也随转动角度不断变化，其路径如图中粗实线所示。由此可见，五轴数控装夹误差的补偿困难正是由于编程旋转中心的偏置矢量OO'随转动不断变化引起的。本文通过扩展指令 G10 X，Y，Z，A，B，C 指定装夹误差，采用动态寻位补偿方法，自动补偿空间变换，保证加工工件空间尺寸精度，而国内许多大型五轴机床无法投入正常使用，就是由于数控系统不具备该功能。

图1 工件装夹偏差示意图

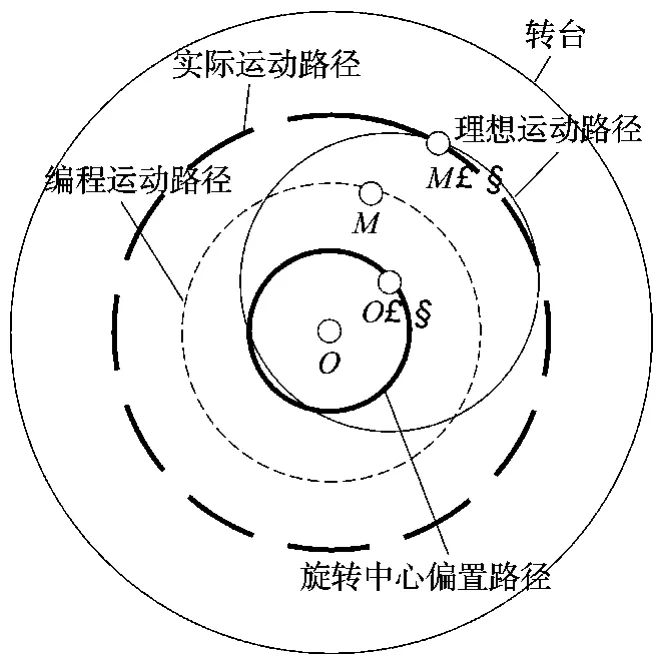
图2 工件随旋转轴转动的运动路径

2 装夹误差动态补偿方法

五轴机床一般包含两个旋转轴，其装夹误差造成的旋转中心偏差也有两组，根据实际机床结构和装夹情况有(x，y，C），(x，z，B），(y，z，A）三种补偿类型。由于五轴数控机床结构形式繁多，坐标转换关系复杂，本文以应用广泛的立式双转台五轴数控机床为例。首先测量工件装夹误差，如图3所示，点O为机床实际旋转中心，在旋转轴角度A=α0，C=β0时测量旋转中心偏差矢量，如图中FAC所示，在旋转轴A，C转动过程中，其角度不断变化，旋转中心偏差矢量方向的变化需要进行机床逆运动变换实时计算，对其进行动态补偿，装夹误差造成的旋转中心偏差计算步骤如下［6］:

以下各符号定义为:

FAC:旋转轴位于A=α0，C=β0时的旋转中心偏差矢量;

FO:旋转轴位于A=0，C=0时的旋转中心偏差矢量;

FA:旋转轴位于A=α，C=0时的旋转中心偏差矢量;

Foffset:旋转轴位于A=α，C=β时的旋转中心偏差矢量;

α0，β0为测量初始装夹误差时的旋转轴角度;α，β为任意角度。

步骤1:计算旋转中心基准矢量FO，即旋转轴在初始状态A=0，C=0时的偏差矢量，将FAC在旋转轴A转动-α0，在旋转轴C转动-β0:

步骤2:计算当旋转轴C无转动，旋转轴A转动任意角度α时的偏差矢量FA;

步骤3:计算当旋转轴A转动任意角度α，旋转轴C转动任意角度β时的偏差矢量Foffset。

由上述(1）～(3）式可计算出加工过程中旋转轴任意角度时的旋转轴中心偏差矢量，在加工运动路径上减去这个偏差矢量，即可动态补偿由于旋转轴偏差矢量变化造成的机床附加运动，消除装夹误差带来的精度问题，加工出与设计一致的工件。

图3 旋转中心装夹误差偏差矢量变换图

3 误差补偿实现与验证

将本文提出的五轴数控加工的装夹误差动态补偿方法在自主研发的数控系统SKYCNC上实现，其处理流程如图4所示。装夹误差参数输入界面如图5所示，在开启装夹误差动态补偿功能后，在上位机中自动计算每个刀位点的旋转中心偏差并补偿，后继的前瞻、插补等均基于补偿后的刀具路径进行。

图4 装夹误差补偿处理流程

图5 装夹误差补偿设定界面

为方便对误差补偿效果的检测，在双转台立式铣床SK5L-70100进行五轴联动精加工直径10cm球体试验，如图6所示。使用通用五轴CAM软件POWERMILL得到五轴NC代码，在旋转轴角度A=0.012，C=0.022时测量得到旋转中心偏差为Xoffset=0.036mm，Yoffset=0.016mm，Zoffset=0.031mm。在无装夹误差补偿时通过测量球体直径得其加工误差为0.052mm;而在装夹误差动态补偿后，加工误差为0.014mm;通过调整装夹精度补偿装夹误差时，不仅耗时较长，而且由于装夹条件限制，其效果也不如数控系统的控制补偿，具体如表1所示。可见，采用本文提出的装夹误差动态补偿方法，既节约了调整装夹精度消耗的时间，也有效消除因装夹误差带来的精度问题。

图6 五轴联动加工球体

表1 球体零件在不同误差处理下的加工效果对比

4 结束语

本文研究了五轴数控加工中的装夹误差对加工精度的影响，分析了旋转中心偏差造成的旋转轴附加运动路径，提出五轴数控的装夹误差动态寻位补偿方法，并将该方法应用于自主开发的SKYCNC中，试验证明，采用该方法可有效补偿五轴机床的装夹误差，消除由此造成的精度问题，提高了机床实际加工效率，具有重要的工程应用意义。

［1］黄筱调，洪荣晶，方成刚，等.大直径环形件空系误差分析及数控加工方法［J］.组合机床与自动化加工技术，2004(11）:57-58.

［2］李显松，熊清平.专用数控机床中的工件定位误差主动补偿技术［J］. 测试技术学报，2003，17(4）:317-319.

［3］张发平，童应学，孙厚芳.工件装夹系统装夹方案误差建模分析技术［J］.北京理工大学学报，2009，29(11）:968-971.

［4］周静，陈慰芳，曲绍朋.数控加工误差主动补偿方法［J］.计算机集成制造系统，2010，16(9）:1902-1907.

［5］刘明灯，陆启建.一种高速高精度皮米插补数控系统［J］. 中国制造业信息化，2006，17:33-36.

［6］胡寅亮，熊涛，黄翔.五轴联动数控机床的后置处理方法［J］. 机械科学与技术，2003，22(7）:175-177.