纳米/微米Cu的力学性能数值模拟

冯广海，杜忠泽，闫 敦，王经涛

(1. 西安建筑科技大学 冶金工程学院，西安 710055；2. 南京理工大学 材料科学与工程学院，南京 210094)

纳米/微米Cu的力学性能数值模拟

冯广海1，杜忠泽1，闫 敦1，王经涛2

(1. 西安建筑科技大学 冶金工程学院，西安 710055；2. 南京理工大学 材料科学与工程学院，南京 210094)

基于复合材料的观点建立纳米/微米Cu细观力学研究模型，采用有限元数值模拟技术对纳米/微米Cu的力学性能进行数值模拟，分析纳米/微米晶的分布、体积分数和形状对纳米/微米 Cu强度和塑性的影响。结果表明：与层状分布相比，立方/球状密封分布的纳米/微米Cu强度和塑性均较大，其塑性随微米晶增韧相体积分数的增大而增大，而屈服强度则逐渐降低；随微米晶增韧相形状因子(有效长径比)的增大，纳米/微米Cu的力学性能表现出明显的各向异性。

Cu；细观力学模型；韧化；有限元分析；数值模拟

晶粒细化不仅能提高室温下金属材料的强度，而且可改善其塑性和韧性，从而显著提高金属材料的综合力学性能，因此，金属材料的晶粒细化受到各国材料研究者的广泛关注[1-5]。自20世纪60年以来，人们采用快速凝固[6-7]、机械合金化[8-9]、剧烈塑性变形[10-11]等工艺将金属材料的内部组织细化至亚微米级(0.1~1 μm)甚至纳米级(1~100 nm)。然而，实验结果表明，绝大多数纳米金属材料，如纳米Cu、Au、Ni、Pd，虽然抗拉强度较同成分粗晶材料提高了3~5倍，但其塑性极低，伸长率仅为1%~2%[12-13]。

一般说来，金属材料的塑性取决于其加工硬化能力和应变速率敏感因子，这两个指数越大，材料在单向拉伸时就越能延迟颈缩，从而显著地提高材料的塑性。由于纳米材料的晶粒非常细小，位错通常在晶界一边弓出而在另一边被吸收，其晶内位错极少，因此，绝大部分纳米材料没有应变硬化现象[14-15]。值得注意的是，最近WANG等[16]在液氮温度下对纯Cu进行冷轧并在123 ℃退火，制备出微米晶(25%，体积分数)，均匀分布于纳米晶基体的纳米/微米 Cu，其强度与纯纳米Cu的相比稍有降低，但塑性得到了极大的改善，从而解决了纳米材料的低塑性问题。本文作者对纳米/微米 Cu的力学性能进行数值模拟，根据复合材料的观点建立了细观力学研究模型，模拟纳米/微米晶的分布、体积比和形状对纳米/微米Cu强度和塑性的影响，为制备具有较高强度和塑性的金属纳米材料提供理论依据。

1 有限元模型的建立

WANG等[16]认为在纳米/微米Cu中纳米晶区具有高强度和低塑性，而微米晶区具有低强度和高塑性，导致纳米/微米Cu与纯纳米Cu相比强度稍低而塑性则显著提高，从而克服了纯纳米 Cu低塑性的缺点。由于纳米Cu和微米Cu的成分相同，但其性能不同，因此，可借助复合材料的观点，将纳米晶区和微米晶区分别视为基体相和增韧相，即将纳米/微米材料视为纳米/微米复合材料，故可借鉴复合材料细观力学的方法建立细观力学研究模型。基体相与增韧相的弹性模量、泊松比和屈服强度列于表 1[17]，塑性变形阶段的应力—应变关系见文献[16]，基体相和增韧相均视为理想弹塑性材料，服从von Mises屈服准则。

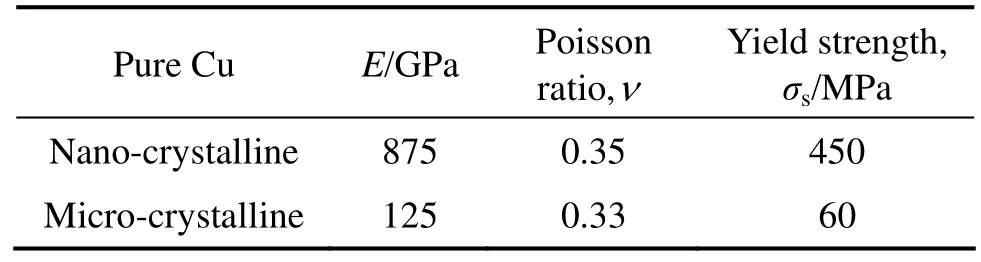
表1 纳米/微米Cu的力学性能[17]Table1 Mechanical properties of nano-/micro-crystalline pure Cu[17]

根据纳米/微米 Cu的组织特征(见图 1(a))和复合材料细观力学模型的基本方法[18]提取代表单元(见图1(b))。一方面，代表单元体的尺度必须足够大，以真实反映复合材料的微观结构特征(增韧相分布、体积分数和形状)；另一方面，代表单元必须远小于宏观物体的尺度以进行细观力学计算与研究。基于上述原则确定代表单元立方体边长为50 μm，增韧相区(微米晶区)的形状分别为球体、立方体和横截面为正方形的长方体。代表单元体的命名采用“X/Y复合单元体”形式，其中：X表示基体相区形状；Y表示增韧相区形状。为了研究增韧相区的分布、体积分数和形状对纳米/微米Cu力学性能的影响，本研究确定两类代表单元，即密闭复合单元(立方体/球体、立方体/立方体、立方体/长方体)和层状复合单元(两相区层状依次叠加)，增韧相体积分数由增韧相区体积与代表单元体体积来确定。

图1 纳米/微米 Cu微观组织及立方体/球体复合单元体模型Fig.1 Microstructures of nano-/micro-crystalline pure Cu (a)and model of cube/sphere unit cell (b)

采用三维有限元商用软件Marc.Superform对代表单元体在定量加载条件下的弹塑性形变进行有限元模拟与计算。根据所采用的代表单元体模型(见图1(b))，充分利用对称性条件，模拟计算的代表单元取图1(b)中1/8模型，对应的有限元模型如图2所示。根据本研究弹塑性有限单元求解所采用的变刚度法中定量加载法原理，结合剖分体内界面的位移对称性条件，对

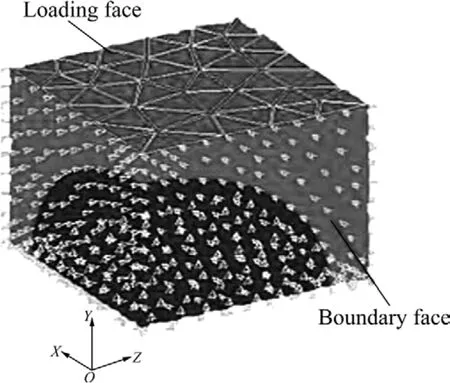
图2 立方体/球体代表复合单元体(1/8部分)的有限元模型及初始网格Fig.2 Finite element model and initial mesh of cube/sphere unit cell (1/8)

代表单元体施加定量载荷，然后通过有限元计算出各计算单元的等效应变与等效应力等，并借助于图形与统计工具, 对这些结果进行整理与分析，得出该代表单元体加载变形过程中应力—应变分布图以及等效应力—等效应变关系曲线。

2 模拟结果及分析

2.1 纳米/微米Cu复合韧化模拟可行性分析

对 WANG 等[16]所制备的纳米/微米 Cu(微米晶相的体积分数约为25%)进行有限元模拟计算，得出等效应力—应变关系曲线如图3所示。由图3可知，计算结果与实验数据曲线吻合较好，表明所提出的细观力学代表单元体模型与有限元平均化计算方法具有一定的合理性和可行性；同时，也从理论计算的角度说明一定体积分数的微米晶相镶嵌于纳米晶相中这种独特混晶组织对改善纳米金属材料的塑性具有可行性，为今后纳米材料优化设计提供了帮助。

值得注意的是，模拟计算结果与实验测得结果仍然存在一定的误差，这可能是由以下两个因素导致的：1)计算过程中未考虑纳米/微米复合材料的实际变形机制，如 KIM 等[19]认为纳米晶材料变形的主要机制是扩散蠕变，采用粘弹塑性有限元方法更能真实地模拟纳米/微米复合材料的变形过程[20-21]，但遗憾的是，目前缺少纳米晶与微米晶 Cu的粘弹塑性本构关系实验数据；2)计算所依据的复合材料细观力学基本假设与实际材料之间存在差异，如立方体/球体复合单元体模型中增韧相采用球体形式，其有效长径比为1，这种几何上的简化处理排除了取向因素的影响，从而掩盖了实际材料中微观组织特征对材料力学性能的影响。

2.2 增韧相分布对纳米/微米Cu韧化的影响

图 4所示为层状与立方体/球体复合单元体(增韧相体积分数相同)在拉伸载荷下的等效应变分布图。由图4可知，与立方体/球体复合单元体相比，层状复合单元体中微米晶区与纳米晶基体之间的变形程度相差很大，即变形的均匀性较差。进一步增大外加应力可能导致增韧相区域出现裂纹，从而降低材料塑性和强度，这表明在纳米晶基体中虽然存在相同体积分数微米晶增韧相，但由于其分布状态不同，纳米/微米复合材料力学性能也不同。层状分布时，微米晶区只在层与层之间受到基体纳米相的有限约束，对整体形变的协调作用较差，从而导致增韧效果较差。

层状与立方体/球体复合单元体(增韧相体积分数相同)的等效应力—等效应变曲线如图5所示。从图5中可知，层状分布与立方体/球体分布相比，其复合单元体的强度和塑性均较低，这是由于层状分布的复合单元中微米晶相与纳米晶相的应变不均匀性大于立方体/球体分布复合单元体的应变不均匀性，纳米晶区处于弹性变形阶段时微米晶区可能已发生了断裂，致使层状分布的纳米/微米复合材料的强度和塑性较低。因此，只有微米晶增韧相弥散分布于纳米晶基体中，使其受到很强的约束，有效降低纳米晶基体相中裂纹尖端的局部应力集中，松弛三向拉应力状态，起到增韧的作用，才能使纳米/微米复合组织得到较高的强度和良好的塑性。

图4 层状与立方体/球体复合单元体的等效应变分布Fig.4 Effective strain distributions of unit cells: (a) Sandwich structure; (b) Cube/sphere unit cell

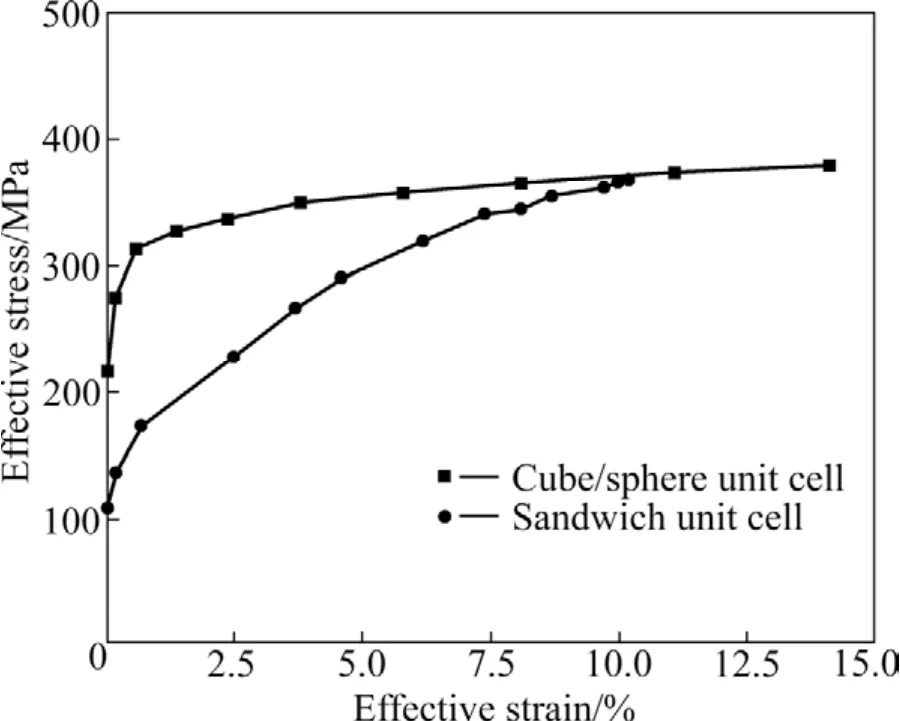
图 5 层状与立方体/球体复合单元体的等效应力—应变曲线Fig. 5 Effective plastic stress—strain curves of sandwich and cube/sphere unit cells

2.3 增韧相形状对纳米/微米Cu韧化的影响

纳米/微米复合材料中微米晶增韧相的形状可能是多种多样，如球形、圆棒状或是针状，因此，有必要对各种形状的微米晶相代表单元体进行模拟计算，以研究增韧相形状对纳米/微米复合材料韧化的影响。图6所示为对立方体/球体、立方体/立方体、立方体/长方体复合单元体(增韧相体积分数均为 35%)进行有限元模拟计算的结果。为简化计算，假设立方体/长方体复合单元体中增韧相长方体X、Y、Z轴长度之比分别为 2∶3∶2 和 3∶2∶2，且均从 Y 轴方向加载。由图 6 可知，在同样的加载条件下，微米晶增韧相形状对纳米/微米复合材料韧化有明显的影响，尤其对于在立方体/长方体复合单元体不同方向加载时，应力分布差别较大，这种差别与非连续短纤维复合材料中沿纤维方向加载和垂直纤维方向加载的情形十分相似；而对于完全对称的立方体/球体和立方体/立方体复合单元体，其应力差很小，这表明微米晶增韧相形状差异会导致纳米/微米复合材料的宏观各向异性。

图 7所示为立方体/球体、立方体/立方体、立方体/长方体 4种代表单元体的平均等效应力—应变曲线。从图 7中可以看出，微米晶增韧相形状对纳米/微米复合材料的力学性能有明显影响。对于完全对称的立方体/球体和立方体/立方体复合单元体，增韧相形状对代表单元整体的性能影响较小；而对于非对称的立方体/长方体复合单元体，增韧相形状的影响很大，且随形状因素的非对称性即增韧相长方体各边长度比值(有效长径比)的增加，这种影响更为显著。这是由于当微米晶增韧相为立方体或长方体时，增韧相与基体接触面存在不连续性即拐角，导致在接触面附近产生较大的应力集中，引起整个代表单元应力增大，使整个代表单元体的强度略有增大。对于立方体和长方体形状的微米晶增韧相，由于增韧相的几何非对称，如长径比(长方体的长度与宽度之比)由 1增加到 1.5时, 复合单元的性能也发生了明显的变化。沿短轴方向，复合单元强度提高了约18%，而塑性下降低了约50%；而沿长轴方向，复合单元强度略有提高(约3%)，且塑性下降不明显。由此可见，改变微米晶增韧相的形状可以调节纳米/微米复合材料的韧性，从而满足纳米晶材料不同的使用目的，实现材料性能的设计与优化。

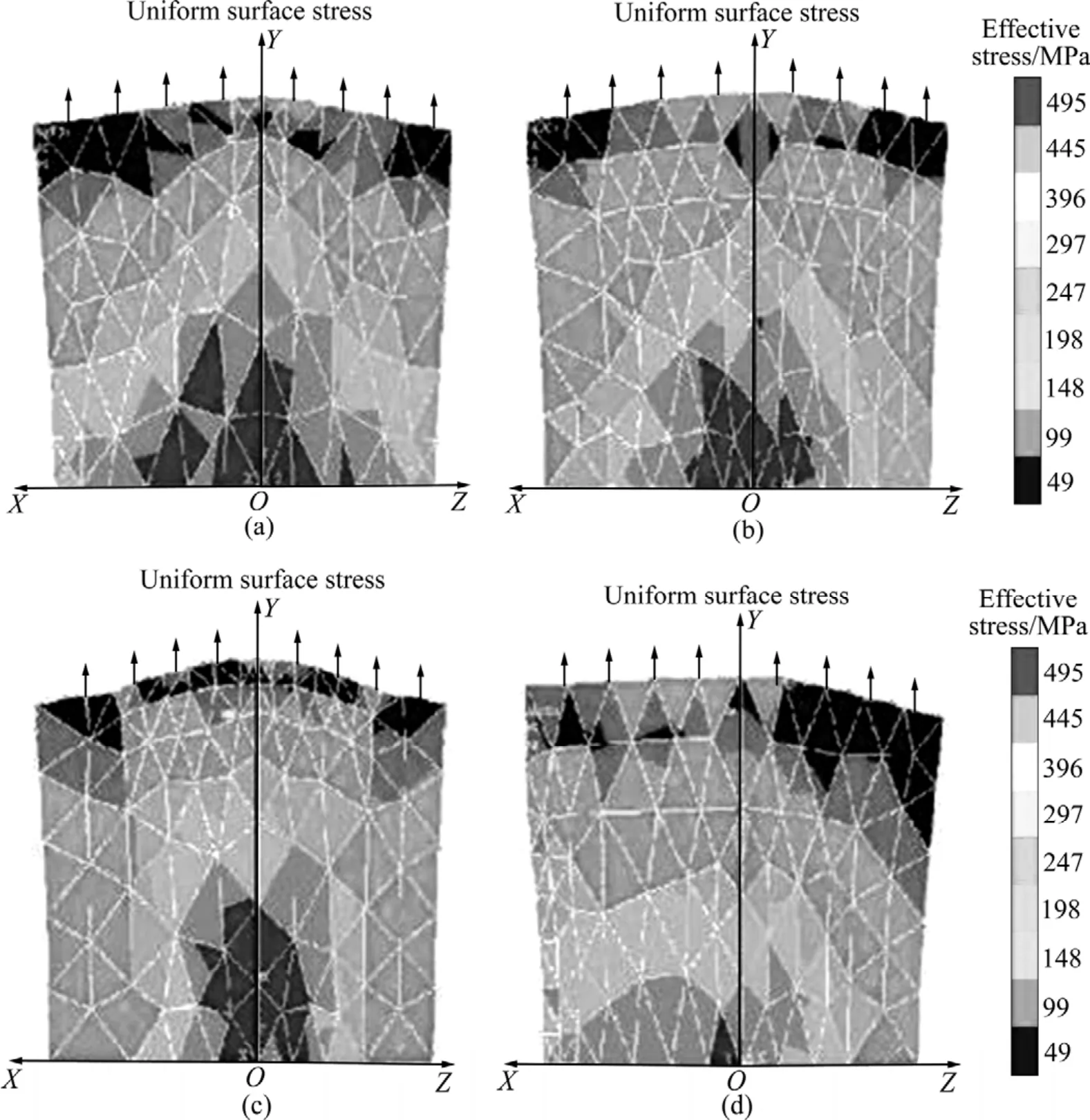
图6 含不同形状增韧相复合单元体的等效应变分布Fig. 6 Effective stress distributions in unit cells of toughening phases containing different shapes: (a) Cube/sphere unit cell;(b) Cube/cube unit cell; (c) Cube/cuboid unit cell loading along long axis; (d) Cube/cuboid unit cell loading along short axis

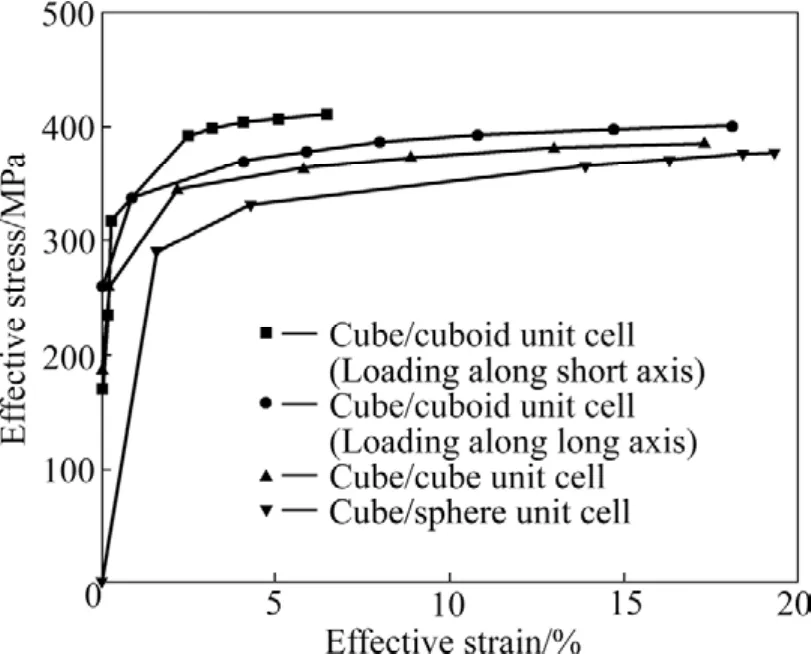
图 7 4种复合单元体(增韧相体积分数为 35%)的等效应力—应变曲线Fig. 7 Effective plastic stress—strain curves of four kinds of unit cells containing 35% (volume fraction) toughening phase

2.4 增韧相体积分数对纳米/微米Cu韧化的影响

图8所示为微米晶增韧相体积分数分别为15%、20%、25%和30%时纳米/微米Cu采用立方体/球体复合单元体的等效应力—应变曲线。由图8可知，微米晶增韧相体积分数对纳米/微米复合材料的力学性能有较大的影响。随着微米晶增韧相体积分数的增大，纳米/微米Cu的屈服强度逐渐降低，而伸长率则增大，这充分体现了微米晶相(软相)对纳米晶基体相(硬相)的增韧作用。

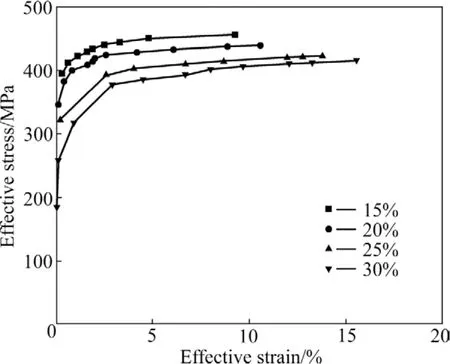
图 8 不同体积分数增韧相立方体/球体复合单元的等效应力—应变关系曲线Fig. 8 Effective stress—strain curves of cubic/sphere unit cells containing different volume fractions of toughening phase

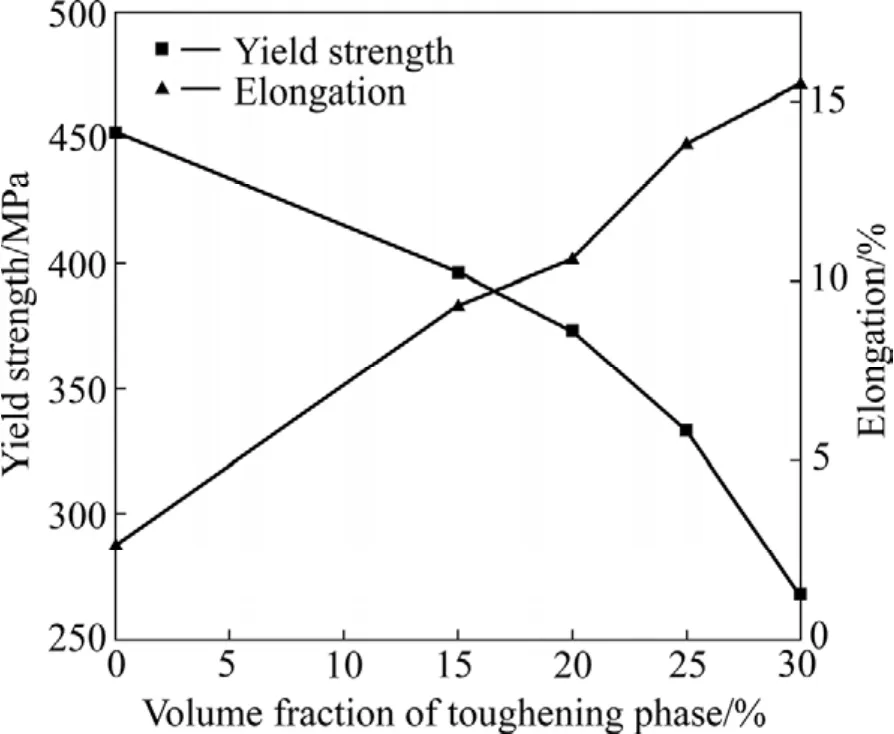
图9 复合单元的屈服强度和伸长率与增韧相体积分数关系Fig. 9 Relationships between yield strength and elongation and volume fraction of toughening phase in cube/sphere unit cells

图9 所示为纳米/微米复合材料的屈服强度和伸长率与增韧相体积分数的关系曲线。从图9可以看出，在复合单元屈服强度降低的同时，塑性并没有得到明显的提高，这可能是有限元计算工具的局限性及求解边界条件、计算终止条件的限制所造成的。由于计算过程中假设代表单元体中两相连接界面为理想连接，两相间没有过渡区域，因此，有限元计算时刚度矩阵的刚度过大，应力集中过快，限制了应变均匀扩展。在实际的复合材料中，界面处组织往往较为复杂，通常存在各种缺陷，而在有限元模拟计算时，为降低研究的复杂性，界面理想连接假设被细观力学中各种计算方法和模型广泛采用，因此，导致目前复合材料细观力学模型在材料力学性能预报方面存在一定的误差。

3 结论

1) 提出用复合材料的观点对纳米/微米Cu进行研究，建立复合增韧细观力学研究模型。通过对该模型在静加载条件下的有限元模拟计算，得到与纳米/微米Cu实际拉伸曲线较为吻合的结果，证实该模型具有一定的合理性与可行性。

2) 层状与立方体/球体复合单元体模拟计算结果表明，在微米晶相(软相)发挥其变形协调作用时，纳米晶基体相(硬相)对其封闭约束是必要条件。增韧相易于塑性变形并能有效降低纳米晶基体相中裂纹尖端的局部应力集中，松弛三向拉应力状态，达到增韧目的，从而提高纳米/微米Cu的塑性。

3) 对于微米晶增韧相弥散分布于纳米晶基体中的纳米/微米 Cu，塑性随微米晶增韧相体积分数的增大而增强，而屈服强度则逐渐降低。随着微米晶增韧相形状因子的增大， 纳米/微米Cu的力学性能表现出更明显的各向异性。

REFERENCES

[1] 杜林秀, 熊明鲜, 姚圣杰, 刘相华, 王国栋. 利用相变进行低碳钢的亚微米化[J]. 金属学报, 2007, 43(1): 59-63.DU Lin-xiu, XIONG Ming-xian, YAO Sheng-jie, LIU Xiang-hua, WANG Guo-dong. Submicroncrystallization of low carbon steels through transformation[J]. Acta Metallurgical Sinica, 2007, 43(1): 59-63.

[2] UTSUNOMIYA H, HATSUDA K, SAKAI T, SAITO Y.Continuous grain refinement of aluminum strip by conshearing[J]. Materials Science and Engineering A, 2004, 372: 199-206.

[3] STOLYAROV V V, ZHU Y T, ALEXANDROV I V, LOWE T C, VALIEV R Z. Grain refinement and properties of pure Ti processed by warm ECAP and cold rolling[J]. Materials Science and Engineering A, 2003, 343: 43-50.

[4] SAKAI G, HORITA Z, LANGDON T G. Grain refinement and superplasticity in an aluminum alloy processed by high-pressure torsion[J]. Materials Science and Engineering A, 2005, 393:344-351.

[5] FARROKH B, KHAN A S. Grain size, strain rate, and temperature dependence of flow stress in ultra-fine grained and nanocrystalline Cu and Al: Synthesis, experiment, and constitutive modeling[J]. International Journal of Plasticity, 2009,25: 715-732.

[6] GUO W H, CHUA L F, LEUNG C C, KUI H W. Formation of bulk nanostructured materials by rapid solidification[J]. Journal of Materials Research, 2000, 15: 1605-1611.

[7] CANTOR B. Nanocrystalline materials manufactured by advanced solidification processing methods[J]. Materials Science Forum, 1999, 307: 143-152.

[8] 李伯林, 朱 敏, 李 隆, 罗堪昌, 李祖鑫. 机械合金化形成的 Fe-Cu纳米晶过饱和固溶体的硬化和软化[J]. 金属学报,1997, 33(4): 420-426.LI Bo-lin, ZHU Min, LI Long, LUO Kan-chang, LI ZU-xin.Hardening and softening effects of Fe-Cu nanocrystalline supersaturated solid solution formed by mechanic alloying[J].Acta Metallurgical Sinica, 1997, 33(4): 420-426.

[9] RAWERS J C. Warm compaction of attrition milled nanostructured iron powders[J]. Nanostructured Materials, 1999, 11:1055-1060.

[10] 邓忠民, 洪友士, 朱 晨. SPD纳米材料制备方法及其力学特性[J]. 力学进展, 2003, 33(1): 56-63.DENG Zhong-min, HONG You-shi, ZHU Chen. Processing method and mechanical properties of SPD nanostructured materials[J]. Advances in Mechanics, 2003, 33(1): 56-63.

[11] VALIEV R Z, ISLAMGALIEV R K, ALEXANDROV I V.Bulk nanostructured materials from severe plastic deformation[J].Progress in Material Science, 2000, 45(2): 103-189.

[12] SANDERS P G, EASTMAN J A, WEERTMAN J R. Elastic and tensile behavior of nanocrystalline copper and palladium[J]. Acta Materialia, 1997, 45: 4019-4025.

[13] NIEMAN G W, WEERTMAN J R, SIEGAL R W. Mechanical behavior of nanocrystalline Cu and Pd[J]. Journal of Materials Research, 1991, 6: 1012-1027.

[14] BUDROVIC Z, SWYGENHOVEN H V, DERLET P M,PETEGEM S V, SCHMITT B. Plastic deformation with reversible peak broadening in nanocrystalline nickel[J]. Science,2004, 304: 273-276.

[15] JIA D, WANG Y M, RAMESH K T, MA E, ZHU Y T,VALIEV R Z. Deformation behavior and plastic instabilities of ultrafine-grained titanium[J]. Applied Physics Letters, 2001, 79:611-613.

[16] WANG Y M, CHEN M W, ZHOU F H, MA E. High tensile ductility in a nanostructured metal[J]. Nature, 2002, 419:912-914.

[17] 铜合金及其加工手册编写组. 铜合金及其加工手册[M]. 北京:冶金工业出版社, 1995: 364.Editorial Group of Copper Alloys and Processing Manual.Copper alloys and processing manual[M]. Beijing: Metallurgical Industry Press, 1995: 364.

[18] 卡恩 R W. 复合材料的结构与性能(第13卷)[M]. 吴人洁, 译.北京: 科学出版社, 1999: 325-328.CAHN R W. Structure and properties of composites (Vol.13).WU Ren-jie, transl. Beijing: Science Press, 1999: 325-328.

[19] KIM H S, ESTRIN Y, BUSH M B. Constitutive modeling of strength and plasticity of nanocrystalline metallic materials[J].Materials Science and Engineering A, 2001, 316: 195-199.

[20] YU J W, CHENG S, LALLIT A. A computational study of the mechanical behavior of nanocrystalline fcc metals[J]. Acta Materialia, 2006, 54: 3177-3190.

[21] YU J W, HUANG G. An elastic-viscoplastic model of deformation in nanocrystalline metals[J]. Materials Science and Engineering A, 2008, 478: 16-25.

Numerical simulation of mechanical properties in nano-/micro-crystalline Cu

FENG Guang-hai1, DU Zhong-ze1, YAN Dun1, WANG Jing-tao2
(1. School of Metallurgical Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China;2. School of Materials Science and Engineering, Nanjing University of Science and Technology,Nanjing 210094, China)

A micro-mechanical model of a nano-/micro-crystalline pure Cu was developed on the basis of the idea of composites. The mechanical properties were analyzed by finite element simulation. The effects of nano-/micro-crystalline distribution, volume fraction and shape on the tensile strength and ductility were investigated. The results indicate that,under uniaxial tensile loading, the tensile strength and ductility in cube or sphere geometry distribution are higher compared to the sandwich geometry distribution. With the increase of microcrystalline volume fraction of toughening phase, the ductility of the nano-/micro-crystalline pure Cu increases and the yield strength decreases. The strength and ductility of the nano-/micro-crystalline pure Cu have an obvious isotropy with the increase of the shape factor of microcrystalline toughening phase.

Cu; micro-mechanical model; toughening; finite element analysis; numerical simulation

TG146.1；TG113.2

A

1004-0609(2012)1-0201-07

国家自然科学基金资助项目(59974018)

2010-12-14；

2011-03-29

冯广海，讲师；电话：029-88460536; E-mail: guanghai_feng@yahoo.com.cn

(编辑 陈卫萍)