火炮制退机节制杆优化设计
2012-11-23顾克秋邵跃林
周 成,顾克秋,邵跃林
(1.南京理工大学 工程训练中心,江苏 南京 210094;2.南京理工大学 机械工程学院,江苏 南京 210094)
在制退机结构确定后对节制杆参数的优化设计即是对后坐阻力的优化设计,对后坐阻力进行优化设计多是为了获得较好的后坐阻力曲线,使其有利于减小架体受力或提高射击稳定性[1-5]。文献[1-3]对节制杆参数优化设计时以后坐阻力峰值最小为优化目标,能够减小最大后坐阻力,但不能获得拟定形状的后坐阻力曲线。笔者采用多目标优化方法,建立节制杆参数优化模型,旨在获得拟定形状的后坐阻力曲线。
1 优化模型的建立
在制退机结构参数获得后,后坐阻力曲线主要由节制杆尺寸参数确定,为了获得理想的后坐阻力曲线,须对节制杆尺寸参数进行优化。本文以拟定的后坐阻力曲线为依据的方法,认为所设计的节制杆尺寸参数计算获得的后坐阻力曲线与拟定后坐阻力曲线符合程度越好,则节制杆设计越成功。完全与拟定后坐阻力曲线吻合是较难实现的,但首先应在后坐长度上有较好的吻合。因此,描述后坐阻力和后坐长度两个指标的目标函数是节制杆尺寸参数优化目标的最基本形式,此属于多目标优化问题。
图1为节制杆尺寸参数示意图[1],本优化中将各段的折点直径d1,d2,…,dn及各段的轴向尺寸x1,x2,…,xn-1作为设计变量,设计变量共有2n-1个。

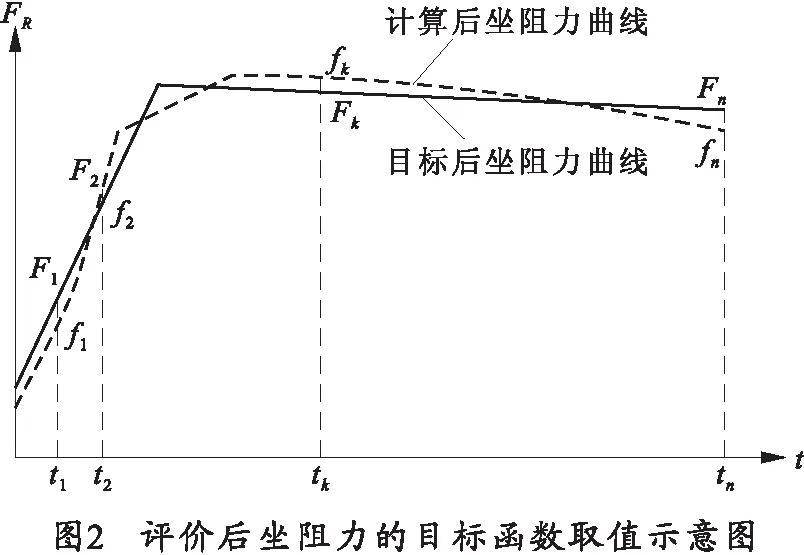
目标函数建立过程方法如下:在拟定后坐阻力曲线时,后坐阻力可表达为后坐长函数的形式,但在使用数值方法进行反面计算时获得的后坐阻力曲线以离散点的形式给出,故直接用函数曲线的形式评价计算所得后坐力的好坏较为困难。本文采用选取多个计算后坐阻力离散点与目标后坐阻力在同一时间点上的值进行对比的形式评价计算所得后坐阻力的优劣,且选取的离散点越多,对后坐阻力的评价越准确,评价后坐阻力取值示意图如图2所示。评价后坐阻力的目标函数定义为:在tn时刻,计算获得的后坐阻力值fn与拟定的目标后坐阻力值Fn之比,应尽量接近1,则以最小化形式表示的目标函数式如下:
(1)
后坐长目标函数可表达为:计算获得的后坐长度λ′与火炮总体结构设计时所要求的后坐长度λ之比尽量接近1,即:
(2)
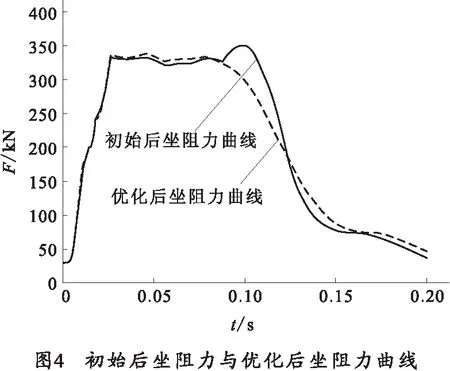
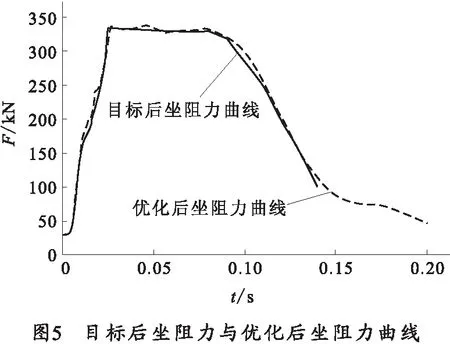
为了在节制杆设计时其径向尺寸不再小于节制杆最小截面直径dxmin,且节制杆能够顺利通过节制环,须对节制杆直径尺寸加以约束;由于设计变量取值范围较大,节制杆每段长度方向尺寸在优化过程中xk的取值有可能会小于xk-1,计算时为了使每次计算都有效,也须约束,使xk-1 本文选择在多体系统动力学软件ADAMS中建立固定炮架形式的反后坐装置计算模型,模型中仅有后坐部分,后坐部分与地面间建立滑移副,模型有1个自由度。采用多学科优化软件ISIGHT集成ADAMS方法建立优化模型,选用非支配排序遗传算法(NSGA-Ⅱ)[6-8]求解优化模型。计算获得的M1(D)、M2(D)的Pareto最优解集[6]如图3,选取图3中A点作为模型的优化解,表1列出了初始设计变量值与优化后获得的优化值,优化后的设计变量取值根据加工工艺经过了圆整。 表1 初始设计变量值与优化后获得的优化解 mm 将初始设计变量值与优化后获得的优化解代入原模型计算,初始后坐阻力与优化后坐阻力曲线如图4,目标后坐阻力与优化所得后坐阻力如图5。 表2列出了初始后坐特性、目标后坐特性与优化后后坐特性值。 表2 初始后坐特性、目标后坐特性、优化后后坐特性 结合表2与图5可知,通过对节制杆尺寸参数的优化可获得拟定形状的后坐阻力曲线,说明本文建立的优化模型可以实现节制杆尺寸参数的优化,这为具有特殊后坐阻力曲线要求的反后坐装置设计提供了可行的设计方法。 对比初始后坐特性、目标后坐特性与优化所得后坐特性表明,本文所建优化模型合理,该优化模型通过对节制杆尺寸参数的优化,可用于获得拟定 形状的后坐阻力曲线。这为具有特殊后坐阻力曲线要求的反后坐装置设计提供了可行的设计方法。 [1] 高树滋,陈运生,张月林,等. 火炮反后坐装置设计[M].北京:兵器工业出版社,1995. GAO Shu-zi,CHEN Yun-sheng,ZHANG Yue-lin,et al.Design of recoil system for guns[M].Beijing:The Publishing House of Ordnance Industry,1995.(in Chinese) [2] 郑小将.驻退机优化设计[D].南京:华东工学院,1990. ZHENG Xiao-jiang. Optimization of the gun recoil mechanism[D]. Nanjing: East China Institute of Technology,1990.(in Chinese) [3] 宗士增,钱林方,徐亚栋. 火炮反后坐装置动力学耦合分析与优化[J].兵工学报,2007(3):272-275. ZONG Shi-zeng,QIAN Lin-fang,XU Ya-don.Dynamic coupling analysis and optimization of gun recoil mechanism[J].Acta Armamentarii,2007(3):272-275.(in Chinese) [4] 李强,郑建国,高树滋.火炮稳定性与后坐阻力R的最优设计[J].火炮发射与控制学报, 1997(1):34-39. LI Qiang,ZHENG Jian-guo,GAO Shu-zi.Optimum design of firing stability and recoil resistance of gun[J].Journal of Gun Launch & Control.1997(1):34-39.(in Chinese) [5] 赵纪华.火炮最优射击稳定性设计研究[J].振动与冲击.2010(11):91-93. ZHAO Ji-hua.Optimal firing stability design for a gun[J]. Journal of Vibration and Shock,2010(11):91-93.(in Chinese) [6] 王晓鹏. 多目标优化设计中的Pareto遗传算法[J]. 系统工程与电子技术,2003,25(12):1558-1561. WANG Xiao-peng. Pareto genetic algorithm for multi-objective optimization design[J].Systems Engineering and Electronics, 2003,25(12):1558-1561.(in Chinese) [7] 吴中元, 关志华, 李光泉.一种改进的非支配排序遗传算法[J]. 北京科技大学学报,2002,24(6): 679-682. WU Zhong-yuan,GUAN Zhi-hua,LI Guang-quan.An improved evolutionary algorithm for multi-objective optimization[J].Journal of University of Science and Technology Beijing, 2002,24(6): 679-682.(in Chinese) [8] 江坤,钱林方,徐亚栋. 某炮口制退器的多目标优化设计[J].系统仿真学报,2007(8):3478-3480. JIANG Kun, QIAN Lin-fang, XU Ya-dong. Multi-objective optimization of a muzzle brake[J].Journal of System Simulation, 2007(8):3478-3480.(in Chinese)2 优化实施与结果分析



3 结 论
