基于双指数跳扩散的三叉树利率模型

李玉萍

(中国矿业大学理学院,中国 徐州 221116)

利率是影响金融市场变化的最基本因子,利率风险来源于利率的随机性.随机与风险在文献[1]中有很好的研究．最简单亦是最常用的利率模型是Vasicek模型[2].比Vasicek模型更一般的是Hull-White模型[3]．为了克服利率可能为负的不足,Cox,Ingersoll和Ross提出了CIR模型[4]．在利率模型中,利率发生跳是利率变化的一个重要特点．1976年Meton首先引入了跳扩散过程,Beliaeva(2008)等[5-8]在Vasicek(1977)短期利率模型中加入了指数跳,Kou(2002)[9]推导出了双指数跳扩散模型,这个模型最大的优点就是允许正跳和负跳．Beliaeva,Nawalkha(2010)[10]用三叉树模型研究了随机波动率下美式利率期权的定价,在文献[10]中作者把三叉树模型应用到了随机利率模型中,并推广为带有一般指数跳扩散的三叉树模型和带有对数正态跳扩散的三叉树模型．国内学者在三叉树方面也取得了一些好的研究成果[11-12]．

本文运用了Kou[9]中的双指数跳扩散模型,并在Beliaeva等[13]的基础上,把CIR过程下的短期利率模型推广为带有双指数跳扩散的三叉树模型,它较一般的指数跳模型的优点就是允许负指数跳,更接近实际市场．在这个模型下给出了随机利率在任意时刻的值,并分析了随机利率对期权定价的影响．本文在第1小节简述了一般的CIR过程的三叉树模型,第2小节推广了带有双指数跳扩散的CIR模型,第3小节则利用了三叉树模型求出扩散节点的概率和跳点的概率,第4小节分析了随机利率对期权价值的影响．

1 基于CIR过程的三叉树模型

在风险中性测度下短期利率的一般CEV过程

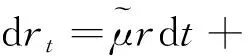
(1)

当p=0.5时,就是CIR模型．Nelso,Ramaswamy(NR)(1990)对上面过程提出了一个路径独立的树图结构变换,并且给出了怎样用变换来构造二叉树．本文推广了NR的方法,用该变换方法来构造CIR过程的三叉树．

由于短期利率的波动项不是常数,NR(1990)提出了一种变换,作X-变换

(2)

对上述方程求反函数,得到短期利率的表达式

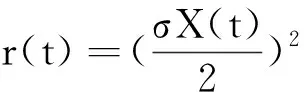
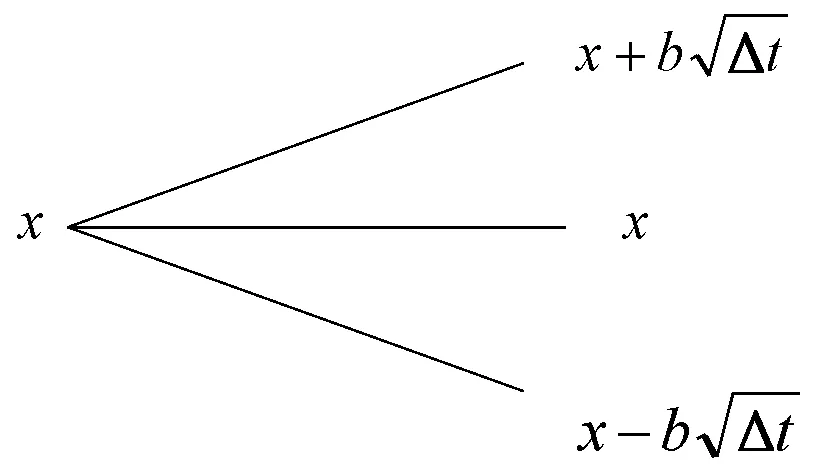
图1 三叉树的节点

这里的INT(•)表示函数的整数部分．

x(t)的上节点,中间节点,以及下节点有如下表示形式

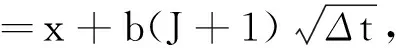
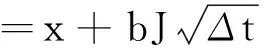
(3)

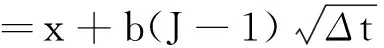
J满足下面表达式

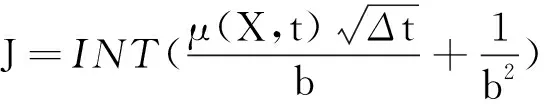
3个扩散节点概率pu,pm,pd的表达式由文[10]中给出,这里就不赘述．

2 CIR过程的双指数跳模型

一般的指数跳只考虑了上跳的可能性忽略了下跳的情况,在这里,我们假设在CIR过程下,短期利率服从双指数跳扩散分布,即

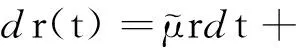
(4)

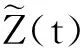
fΥ(y)=pη1e-η1yΙ{y≥0}+qη2e-η2yΙ{y<0}，η1>0,η2>0,

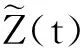
在风险中性测度下,我们可以用下面的短期利率模型

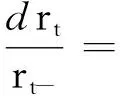
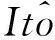
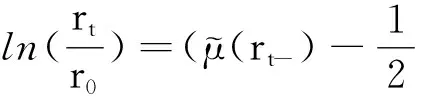
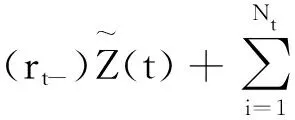
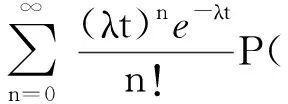
(5)

其中a为任意实数．

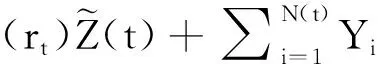
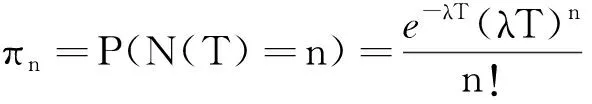
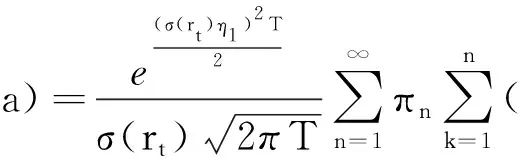
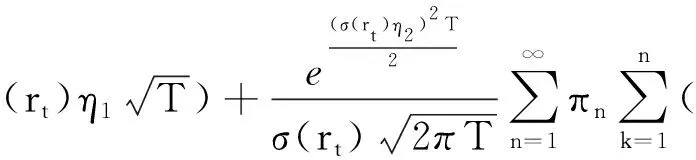
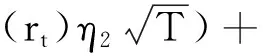
(6)

3 CIR过程的双指数跳扩散树模型

为了模拟带有双指数跳的短期利率,我们用下面的近似值

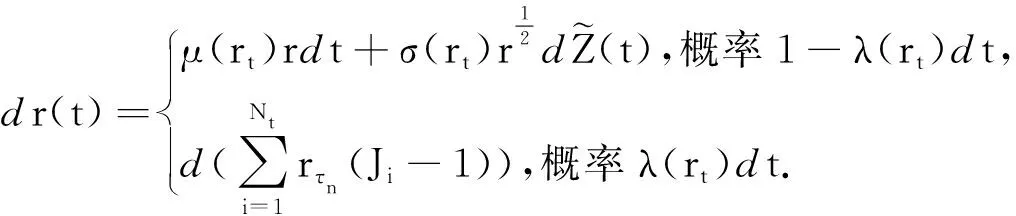
把[0,T]区间n等分,每个小区间为Δt,为了使分析具有一般性,我们考虑任意时刻t=iΔt的节点r(t)(如图2),i=0,1,2,…,n-1,在时刻(i+1)Δt,r(t)的M个不同的值表示为

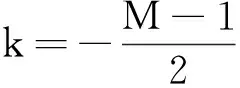
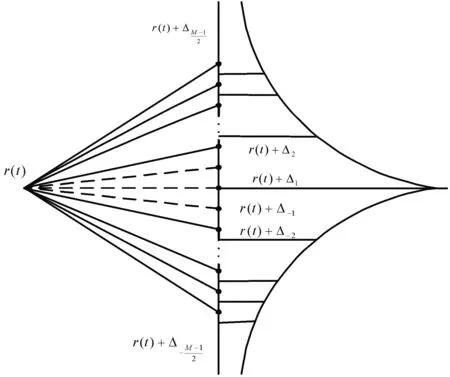
图2 用双指数曲线模拟跳扩散的节点

3.1 扩散点概率

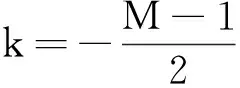
3.2 跳点的概率

第1步,先考虑去掉第1个上跳节点、第1个下跳节点、最顶部的跳点和最底部的跳点．那么

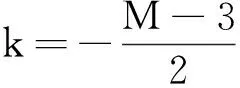
其中，P{Z(T)≥a}由(6)式定义,且

第2步,考虑最顶部和最底部跳点的概率.

顶部跳点的概率可表示为

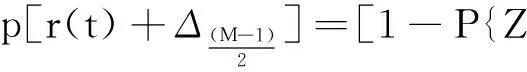
其中

同理,底部跳点的概率可以表示为

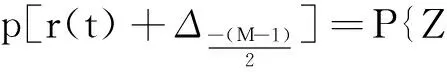
其中

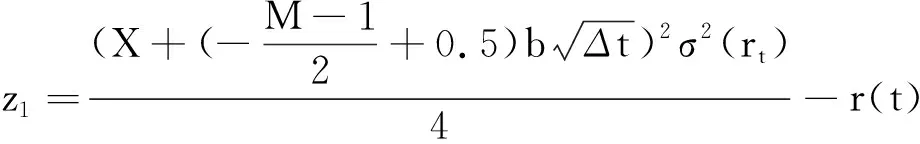
第3步,考虑第1个上跳节点和第1个下跳节点的概率．

第1个上跳节点的概率可以表示为

p[r(t)+ΔJ+2]=[P{Z(Δt)≥z1}-P{Z(Δt)≥z2}]λΔt,

其中

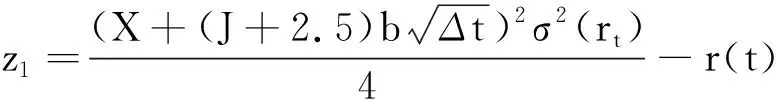
第1个下跳节点的概率可以表示为

p[r(t)+ΔJ-2]=[P{Z(Δt)≥z1}-P{Z(Δt)≥z2}]λΔt,

其中

4 在期权定价中的应用

如图2,r(t)在Δt后的M个节点的值可以表示为

⋮ ⋮

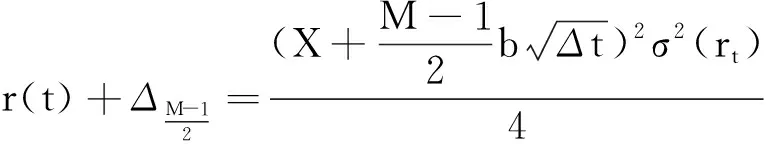
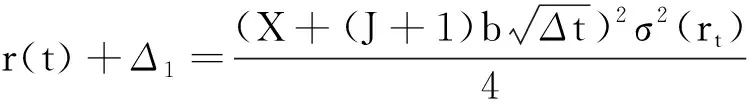
r(t), 概率记为p0,

⋮ ⋮

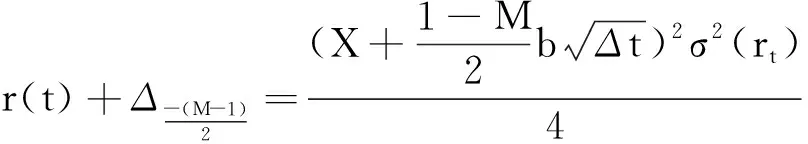
所以,Δt时间后r(t)的值可近似为

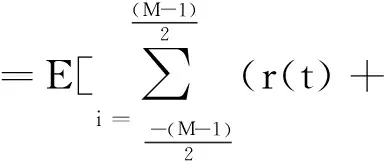
(7)

1973年,Black和Schoes推导出了欧式看涨期权的定价公式:

Ct=StN(d1)-Ke-rtN(d2),

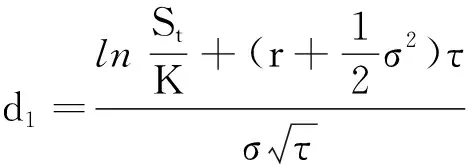
B-S公式中假设利率为常数,即无风险利率,但在实际市场中利率却是随机变化的,存在一定的风险．有了利率的三叉树跳扩散模型后,就可以利用(7)式对某个时刻的利率进行估计,将上面的期权定价模型中的常利率改为利用三叉树跳扩散模型计算出来的随机利率,使期权价值的计算结果更接近实际市场．

图3给出了不同利率波动率下股票价格与期权价值变化关系,该结果为期权定价研究提供了理论依据．

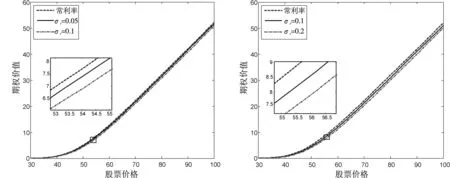
图3 随机利率对期权价值的影响

5 总结

本文引用了Kou(2002)文章中推导的双指数跳扩散模型,推广了Beliaeva,Nawalkha(2011)中的结果,并用三叉树模型求出了跳点的概率,给出了任意时刻的利率值．文章最后通过数值试验分析了随机利率对期权价值的影响.结果表明:利率随机性及利率波动率的大小对欧式期权的定价是有影响的,随机利率模型下期权的价值要比常利率下期权的价值低,并且利率的波动率越大,对期权的价值影响越大,期权的价值就越低．

参考文献:

[1] 欧 辉, 李代绪, 杨向群. 债券价格随机时重设型熊市认售权证的定价[J]. 湖南师范大学自然科学学报, 2011,34(6):16-20.

[2] VASICEK O. An equilibrium characterization of term structure[J]. J Financial Econ, 1977,5(2):177-188.

[3] JOHN H C, WHITE A. Pricing interest rate derivative securities[J]. Rev Financial Stud, 1990,3(4):573-592.

[4] JOHN C, JONATHAN E, STEPHEN A. An intertemporal general equilibrium model of asset prices and theory of the term structure of interest rates[J]. Econometrica, 1985,53(2):363-407.

[5] BAZ J, DAS S R. Analytical approximations of the term structure for jump-diffusion processes: a numerical analysis[J]. J Fixed Income, 1996,6(1):78-86.

[6] DAS S R, FORESI S. Exact solutions for bond and option prices with systematic jump risk[J]. Rev Derivatives Res, 1996,1(1):7-24.

[7] CHACKO G, DAS S R. Pricing interest rate derivatives: a general approach[J]. Rev Financial Stud, 2002,15(1):195-241.

[8] BELIAEVA N A, NAWALKHA S K, SOTO G. Pricing American interest rate options under the jump-extended Vasicek model[J]. J Derivatives, 2008,16(1):29-43.

[9] KOU S G. A jump diffusion model for option pricing[J]. Manag Sci, 2002,48(1):1086-1101.

[10] BELIAEVA N A, NAWALKHA S K. A simple approach to pricing American options under the Heston stochastic volatility model[J]. J Derivatives , 2010,17(4):25-43.

[11] 韩立杰, 刘喜波, 刘 宇. 期权定价的新型三叉树方法[J]. 数学实践与认识, 2007,37(18):39-42.

[12] 姚落根, 欧 辉, 杨向群. 单周期三叉树模型中等价鞅测度的比较[J]. 湖南师范大学自然科学学报, 2009,32(1):11-14.

[13] BELIAEVA N, NAWALKHA S. Pricing American interest rate options under the jump-extended constant- elasticity- of-variance short rate models[J]. J Banking Finance, 2012,36(1):151-163.