二维不可压缩层流模型数值解与稳定性

肖润梅,明亚东,李秀兰

(山西大同大学数学与计算机科学学院,中国 大同 037009)

层流流体稳定性问题的研究长期以来一直倍受数学家的关注．当雷诺数在某个特定范围内逐步增大时，流体将经历一个由层流向紊流转换的特殊过程[1]，即由一个稳定的、亚临界的层流流体转化成为一个超临界的紊流流体．为此，通过对流体雷诺数和波长的计算来预测层流的稳定性问题变得尤为重要．目前，人们通过对层流流体加入微小外部扰动来预测层流流体稳定性的方法已被广泛地接受[2]．如果在此过程中，外部扰动能够逐渐减弱直至消失，那么流体将继续保持稳定．反之，如果这些外部的扰动随着时间的推移逐渐增大，那么流体将经历一个由层流向紊流流动转化的过渡过程．

层流流体的稳定性问题可归结为Orr-Sommerfeld方程求解问题，该方程的求解在数学界引起了广泛的兴趣．Davey[3]通过有限元的方法来求解Orr-Sommerfeld方程，取得了良好的结果．然而由于有限元方法本身的局限性，运算精度会受到很大的限制．如在计算误差(Δx)p渐进减小的过程中，运用有限元方法只能得到一些有限的p值，同时计算时间过长，不适合广泛运用于求解此类问题．切比雪夫多项式在逼近理论中有重要的应用．第一类切比雪夫多项式的根(被称为切比雪夫节点)可以用于多项式插值．相应的插值多项式能最大限度地降低龙格现象，并且提供多项式在连续函数的最佳一致逼近．Orszag[4]运用切比雪夫多项式以及QR矩阵特征值算法所计算的结果有着较高的计算精度以及较少的计算时间．

当前，谱方法已成为计算流体力学领域的三大主流数值方法之一，并受到广大学者的关注．它是上世纪70年代发展起来的一种数值求解偏微分方程的方法，该方法在理论上具有“无穷阶”收敛性，可采用快速算法，现已被广泛用于气象、物理、力学等诸多领域，成为继差分法和有限元法之后又一种重要的数值方法[5-7]．由于谱方法的“无穷阶”收敛性且具备高的计算精度，相对于有限元方法和切比雪夫多项式的方法，它能够对误差形成指数型收敛，提高了计算精度并缩短了计算时间，为求解Orr-Sommerfeld方程提供了新的思路.

本文运用谱方法的数值分析，以Poiseuille流动为例对Orr-Sommerfeld方程进行了展开与数值计算，并利用计算结果对层流流体的稳定性进行了分析讨论，并验证了谱方法的高精度性和快速收敛性．

1 Orr-Sommerfeld方程数值计算

关于影响层流流动稳定性的因素，主要认为是当流体流经涡轮压气机和管道时，由于入口处粗燥的壁面所造成的边界层流的影响以及外部诸因素对流体的干扰．因此，研究层流流动例如Poiseuille流动的稳定性问题时，可归结为求解Orr-Sommerfeld方程的数值解问题．忽略加速流体过渡过程的外部干扰以及由于压力差造成的过渡过程，并假设其为零压力梯度场的稳定流体，即限制研究对象为：具有一定雷诺数的，零压力场的，二维不可压缩稳定流体．采用线化小扰动理论，可得到一个四阶线性的Orr-Sommerfeld常微分方程

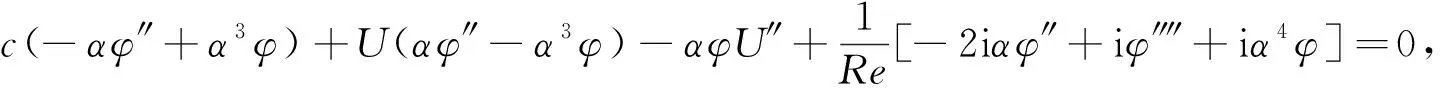
(1)

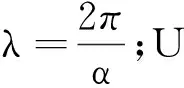
φ(1)=0；φ′(1)=0，

φ(-1)=0；φ′(-1)=0，

(2)

无量纲Poiseuille流动的速度分布为U(y)=1-y2.

对于上述方程，我们并不能求得它的解析解，只能通过数值计算的方法来求出它的数值解．谱方法的主旨思想是将方程在固定的物理空间进行了离散化．通过这样的方式，就可以更加轻松地去处理方程中的一些非线性的变量．首先，通过使用多项式Chebyshev-Gauss-Lobatto nodes[8]对方程的一阶导数进行插值可以得到

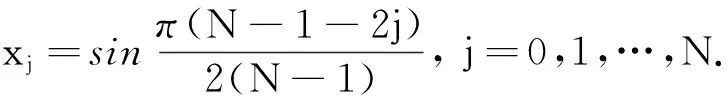
(3)

由于在区间x∈[-1,1]上φ(x)为连续函数，所以通过构建N阶多项式Lk(xj)对φ(x)进行插值Lk(xj)=δjk.

(4)

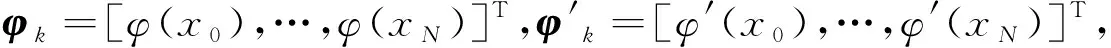
结合边界条件，可得

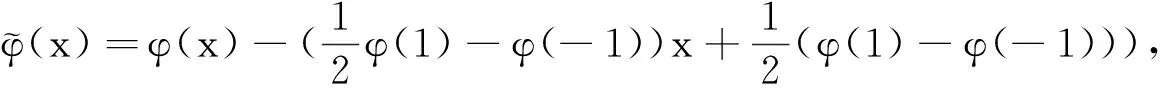
(5)

最后得到方程

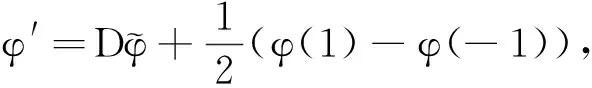
(6)

在此，需要对切比雪夫微分矩阵D引入三角恒等式，可得

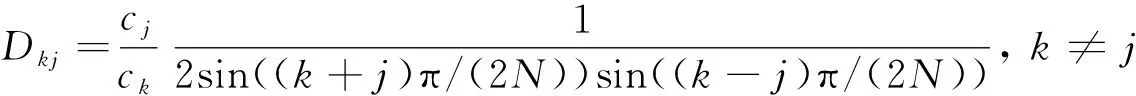
(7)

(8)

(9)

(10)

把以上等式代入Orr-Sommerfeld 方程可以得到2个不同的矩阵

A=(D4-2D2+I)/Re-2iaI-idiag(1-x2)(aD2-a3I),

B=-iaD2+a3I.

(11)

D4、D2分别为矩阵D的四阶和二阶导数矩阵；I为单位矩阵．那么从方程(11)得到特征值c满足

Aφk=cBφk.

(12)

2 数值计算结果分析

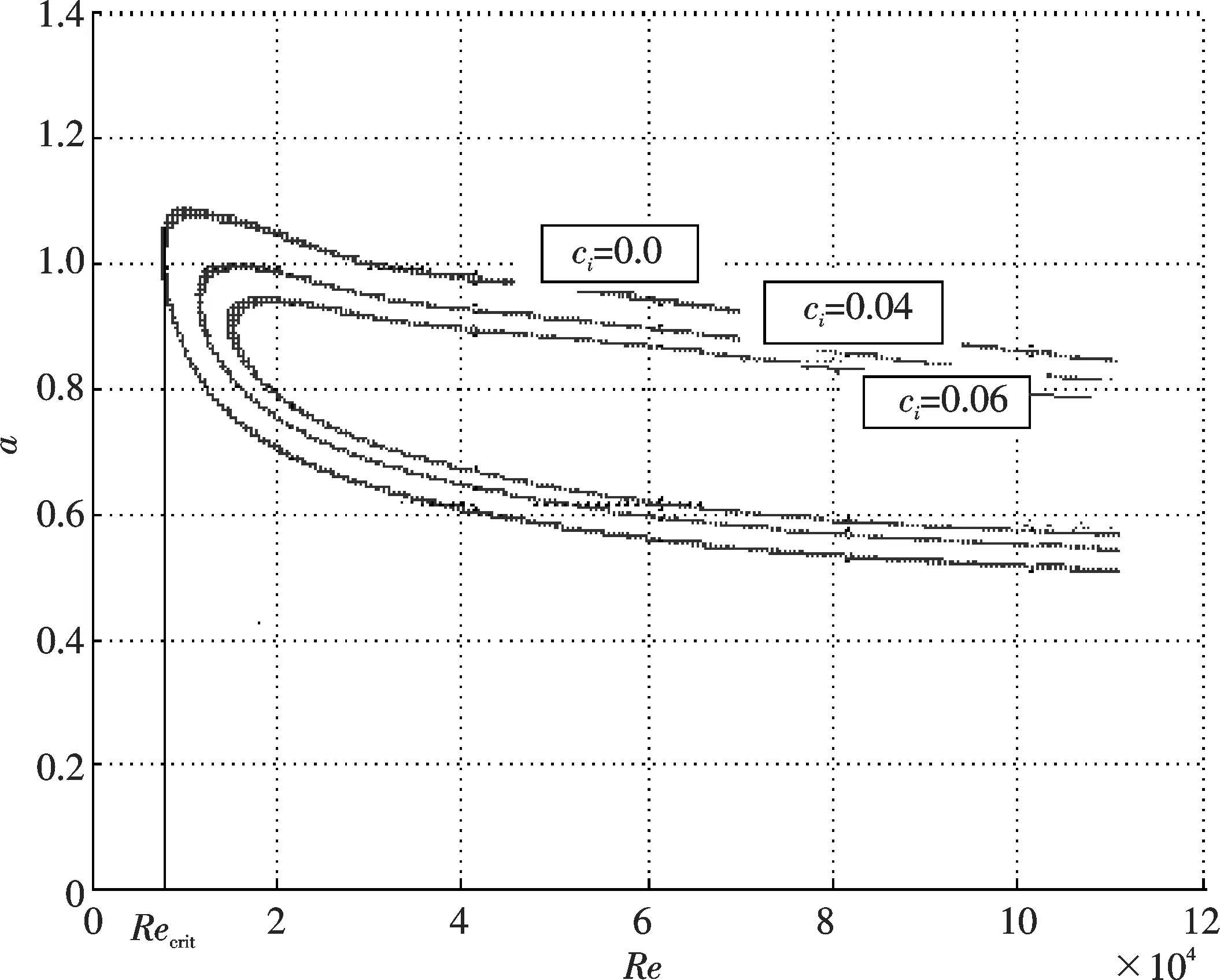
图1 Poiseuille流动稳定性计算图

求解方程(12)的特征值c，需要给定α和Re值．如果ci<0，那么层流流动将保持稳定，相反地，如果ci>0，那么层流流体就会向紊流进行转化，ci=0表示临界稳定状态．图1表示了ci随Re和α值变化的曲线(具体计算程序见附录1)．

图中分别显示了ci=0.0，ci=0.04，ci=0.06的等值线．从图中可以看出由等值线ci=0.0所包围的中间区域为不稳定区, 也就是说当Re和α的值在这个范围内时, 层流流体是不稳定的，极易向紊流进行转化．等值线ci=0.0外围被视为稳定区域．同时可以得到临界的雷诺数值为Recrit=5 773，也就是说如果当流体的雷诺数小于5 773时，无论α取值多少，流体始终保持层流流动．同时在临界雷诺数处，首先产生不稳定流体的αc=1.02．对于本文得到的临界数值可以与其他文献所得到的值进行比对，Thomas[9]运用有限元的方法得到Recrit≈5 780，αc=1.026．Orszag[4]通过切比雪夫多项式的方法得到Recrit≈5 772，αc=1.021．由此验证了通过谱方法求解Orr-Sommerfeld equation有着很高的计算精度以及较少的计算时间，为解决此类方程提供了新的思路．

附录1

TheComputerprogramming

function [x, DL] = cheb2nddif(N, Dem)

I = eye(N);

Lk = logical(I);

N1 = floor(N/2);

N2 = ceil(N/2);

k = [0:N-1]′;

theta = k*pi/(N-1);

x = sin(pi*[N-1:-2:1-N]′/(2*(N-1)));

t = repmat(theta/2,1,N);

Dx = 2*sin(t′+t).*sin(t′-t);

Dx = [Dx(1:N1,:); -flipud(fliplr(Dx(1:N2,:)))];

Dx(Lk) = ones(N,1);

c = toeplitz((-1).^k);

c(1,:) = c(1,:)*2; c(N,:) = c(N,:)*2;

c(:,1) = c(:,1)/2; c(:,N) = c(:,N)/2;

delta = 1./Dx;

delta(Lk) = zeros(N,1);

D = eye(N);

for i = 1:Dem

D = i*delta.*(c.*repmat(diag(D),1,N) - D);

D(Lk) = -sum(D′);

DL(:,:,i) = D;

End

function [x, D4] = cheb4thdif(N)

I = eye(N-2);

Lk = logical(I);

N1 = floor(N/2-1);

N2 = ceil(N/2-1);

k = [1:N-2]′;

theta = k*pi/(N-1);

x = sin(pi*[N-3:-2:3-N]′/(2*(N-1)));

r = [sin(theta(1:N1)); flipud(sin(theta(1:N2)))];

gamma = r.^4;

lamda1 = -4*r.^2.*x./gamma;

lamda2 = 4*(3*x.^2-1)./gamma;

lamda3 = 24*x./gamma;

lamda4 = 24./gamma;

B = [lamda1′; lamda2′; lamda3′; lamda4′];

t = repmat(theta/2,1,N-2);

Dx = 2*sin(t′+t).*sin(t′-t);

Dx = [Dx(1:N1,:); -flipud(fliplr(Dx(1:N2,:)))];

Dx(Lk) = ones(N-2,1);

rr = r.^2.*(-1).^k;

R = rr(:,ones(1,N-2));

c = R./R′;

delta = 1./Dx;

delta(Lk) = zeros(size(x));

Z = delta′;

Z(Lk) = [];

Z = reshape(Z,N-3,N-2);

W = ones(N-3,N-2);

D = eye(N-2);

for i = 1:4

W = cumsum([B(i,:); i*W(1:N-3,:).*Z]);

D = i*delta.*(c.*repmat(diag(D),1,N-2)-D);

D(Lk) = W(N-2,:);

DL(:,:,i) = D;

end

D4 = DL(:,:,4);

N=32;

i = sqrt(-1);

a=0.1:0.01:1.2;

R=1:500:120000;

for k=1:length(a)

for j=1:length(R)

[x,DM] = cheb2nddif(N+2,2);

D2 = DM(2:N+1,2:N+1,2);

[x,D4] = cheb4thdif(N+2);

I = eye(size(D4));

A = (D4-2*D2+I)/R(j)-2*a(k)*i*I-i*diag(1-x.^2)*(a(k)*D2-a(k)^3*I);

B = -i*a(k)*D2+i*a(k)^3*I;

e = eig(A,B);

[m,l] = min(abs(imag(e)));

res(k,j)=imag(e(l));

end

参考文献：

[1] SCHOBEIRI M T. Fluid mechanics for engineers[M]. Berlin:Springer-Verlag, 2010.

[2] DAVEY A, DRAZIN P G. The stability of poiseuille flow in the pipe[J]. J Fluid Mech, 1969,36(02):209-218.

[3] DAVEY A, NGUYEN H P F. Finite-amplitude stability of pipe flow[J]. J Fluid Mech, 1971,45(04):701-720.

[4] ORSZAG S A. Accurate solution of the orr-sommerfeld stability equation[J]. J Fluid Mech, 1971,50(04):689-703.

[5] 尚新民. 谱方法的数值分析[M]. 北京：科学出版社, 2000.

[6] CANUTO C, HUSSAINI M Y, QUARTERONI A,etal. Spectral methods in fluid dynamics[M]. Berlin:Springer-Verlag, 1993.

[7] BALTENSPERGER R, TRUMMER M R. Spectral differencing with a twist[J]. Siam J Sci Comput, 2002,24(5):1465-1487.

[8] DON W, SOLOMONOFF S. Accuracy and speed in computing the chebyshev collocation derivative[J]. Siam J Sci Comput, 1995,16(6):1253-1268.

[9] THOMAS L H. The stability of plane poiseuille flow[J]. Phys Rev, 1953,91(4):780-783.