基于SVM的Web服务质量评价方法

汪海涛,余松森,冼广铭

(1.广东科贸职业学院信息工程系,广东 广州 510640;2.华南师范大学南海校区,广东 广州 510640)

现实生活中很多问题是模糊的和近似的,因此模糊决策在解决实际工程问题方面有重要的作用[1].采用多层模糊综合评价方法对Web服务质量进行评价,其实质是按照结果向量B的排序.在B=W×R中,W称为权重向量,它体现了各个因素的重要性,Wi越大则第i个因素越重要,向量W对评价结果具有重要的影响[2].多层模糊综合评价方法中对加权向量和评价矩阵的确定包含了很大的主观因素,为了减少主观因素的作用,可采用SVM分类方法,提高评价结果的客观性.SVM是一种新型的统计学习方法,能够对分类和模式识别问题进行较大的改进.SVM能够减少归一化参数集,与其他统计决策方法相比,有更好的性能,即使在样本个数很小的时候,也能获得较高的准确率[3].本文中采用SVM综合评价Web服务质量：根据构建Web服务质量的各项评价指标,通过训练构建分类超平面,对其进行二值分类.

1 模糊综合评价方法

1.1模糊评价方法模糊评价是通过构造等级模糊子集把反映被评事物的模糊指标进行量化(即确定隶属度),然后利用模糊变换原理对各指标进行综合.

评价步骤如下：

(1)确定评价对象的因素论域：设有P个评价指标,定义u={u1,u2,…,up}.

(2)确定评语等级论域：v={v1,v2,…,vp},即等级集合,每一个等级可对应一个模糊子集.

(3)建立模糊关系矩阵R.在构造了等级模糊子集后,要逐个对被评事物从每个因素ui(i=1,2,…,p)上进行量化,即确定从单因素来看被评事物对等级模糊子集的隶属度R|ui,进行得到模糊关系矩阵：矩阵R中第i行第j列元素rij,表示某个被评事物从因素ui来看对vj等级模糊子集的隶属度.一个被评事物在某个因素ui方面的表现,是通过模糊向量(R|ui)=(ri1,ri2,…,rim)来刻画的.

(5)合成模糊综合评价结果向量.利用合适的算子将权向量A与各被评事物的模糊矩阵R进行合成,得到各被评事物的模糊综合评价结果向量B,即A∘R=B,它表示被评事物从整体上看对等级模糊子集的隶属程度.

(6)对模糊综合评价结果向量进行分析,最常用的方法是最大隶属度原则.

1.2模糊变换给定一个模糊矩阵R和一个模糊向量A：R=(rij)n×m(0≤rij≤1),A=(w1,w2,…,wn),0≤wi≤1(i=1,2,…,n),则称A∘R=B=(b1,b2,…,bn)为模糊变换.

该模型中的ai起加权作用,但主因素的作用仍然突出.

该模型中的wi起过滤作用,削弱了主因素的作用.

在加权平均算法中按照普通矩阵乘法计算权向量与评价矩阵的乘积.该模型在评价向量中包括了所有因素的共同作用,是一种真正意义上的综合.

2 SVM综合评价方法

SVM综合评价方法涉及到几个方面：从训练样本中选择支持向量；构造基于SVM综合评价模型[4](图1所示)；对未知类别的样本进行评价.实验总共采用50个样本,从中选择30个样本作为学习样本,20个用于评价.采用RBF核函数,将训练样本各级因素指标的隶属度代入公式

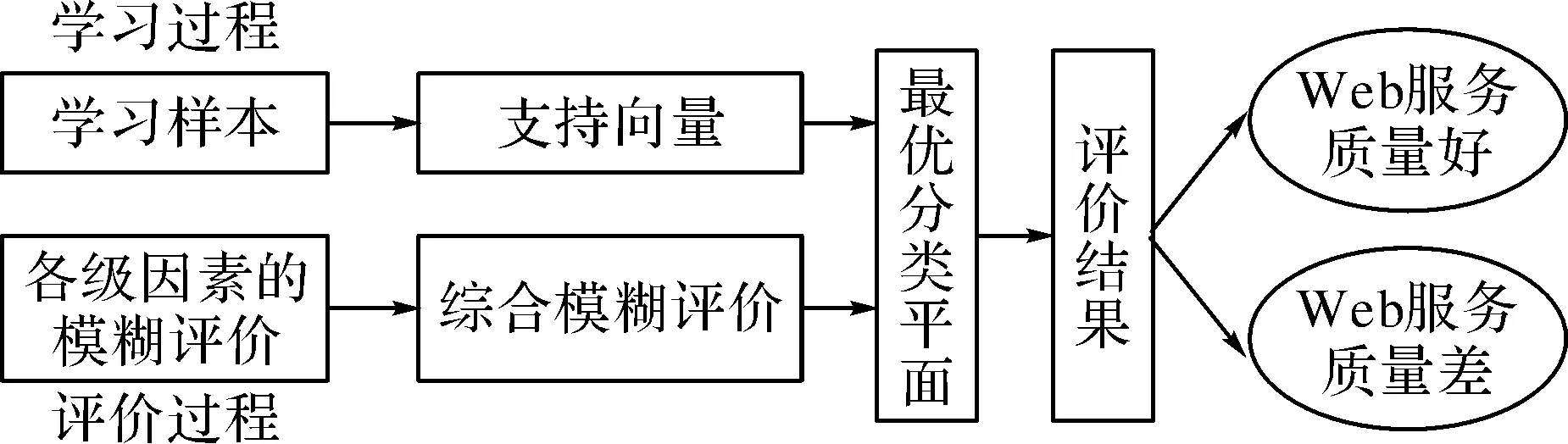
图1 SVM综合评价模型

对该式进行求解可得的支持向量集和各支持向量对应的Lagrange系数,并把它们代入公式

即可获得最优分类超平面.

有如下评价结果：

y=W·X+b≥0,X的Web服务质量好;y=W·X+b<0,X的Web服务质量差.

为了进一步提高评价模型的精度,可以做出如下的改进：

W·X+b≥M1,X的Web服务质量好;M2≤W·X+b≤M1,重新对X进行测试评价;W·X+b

其中-1

3 实验结果与分析

研究问题：对6个Web服务质量好的样本和10个Web服务质量差的样本的综合评价值B(TestVAR)进行测量,状态变量(StateVAR)为1的表示Web服务质量好,为0的表示Web服务质量差.利用ROC曲线分析,多层模糊综合评价值B和支持向量机方法对Web服务质量评价的有效性，下面为实验结果对比：图2为多层模糊综合评价方法的ROC曲线,图3为SVM方法的ROC曲线.表1是多层模糊综合评价和SVM方法下ROC曲线下面积图.

图2 多层模糊综合评价方法的ROC曲线

图3 SVM方法的ROC曲线

表1多层模糊综合评价和SVM方法的ROC曲线下面积

实验结果变量：测试变量

面积标准误差渐近信号95%渐近置信区间上界下界多层模糊评价方法0.6750.1360.2550.4080.942SVM方法0.8120.0350.0000.7440.881

测试结果：测试变量在正实际状态组和负实际状态组间至少有一个约束,统计值也许有些偏差.a.非参数假设下;b.零假设:实际面积=0.5.

多层模糊综合评价方法的ROC曲线和曲线下的面积分析结果如下：图2为多层模糊综合评价方法的ROC曲线,ROC曲线下的面积AZ=0.675(0.5

采用SVM方法按照“Web服务质量好(1)”,“需要重新评价(2)”和“Web服务质量差(3)”,对45份Web服务质量好组的样本和对102份对照组的样本进行评价,图3为SVM方法的ROC曲线,ROC曲线下的面积AZ=0.812,标准差(Std. Error)=0.035,95%的置信区间的相伴概率(Asymptotic Sig.)=0.000,P<0.01,95%的置信区间(Asymptotic 95% Confidence Inerval)为(0.744, 0.881),不包含0.5,表明用SVM方法评价Web服务质量好坏的准确性是较高的.

[1] Syau YuRu, Lee E Stanley. Preincavity and fuzzy decision making[J].Fuzzy Sets and Systems,2005,15(3):408-424.

[2] 李鸿吉.模糊数学基础及实用算法[M].北京：科学出版社,2005.

[3] Millet-Roig J, Ventura-Galiano R, Chorro-Gasco F J, et al. Support vector machine for arrhythmia discrimination with wavelet-transform-based feature selection[J].Computers in Cardiology,2000(4):407-410.

[4] 肖健华,吴今培,杨叔子.基于SVM的综合评价方法研究[J].计算机工程,2002,28(8):28-30.

[5] 陈丽,陈静.基于支持向量机和k-近邻分类器的多特征融合方法[J].计算机应用,2009,29(3):833-835.

[6] 崔建,李强,刘勇.基于模糊分类关联规则的支持向量机分类器生成方法[J].计算机应用,2011,31(5):1348-1350.

[7] 彭光金,司海涛,俞集辉.改进的支持向量机算法及其应用[J].计算机工程与应用,2011,47(18):218-221.

[8] 徐立祥,罗斌,谢进.一种改进的再生核支持向量机回归模型[J].计算机工程与设计,2011,47(24):100-102.