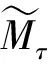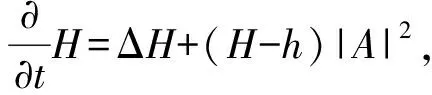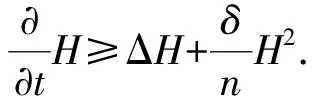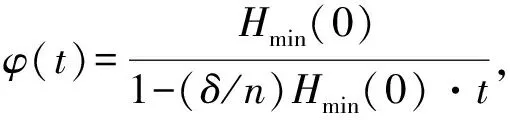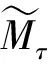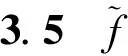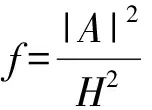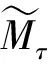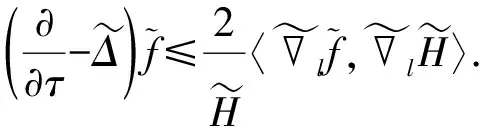具有平衡项的平均曲率流
2012-11-22田大平喻丽菊
田大平,喻丽菊
(1.江汉大学数学与计算机科学学院,湖北 武汉 430056; 2.嘉兴学院数理与信息工程学院,浙江 嘉兴 314001)
0 引言
设Mn是n(n≥2)维光滑紧致无边流形,X0:Mn→Rn+1是Mn到Rn+1的光滑浸入,考虑关于方程
(0.1)
的光滑映射Xt=X(·,t).其中H是Mt=Xt(Mn)的平均曲率,v是单位外法向量,h(t)是[0,∞)的非负光滑函数.方程(0.1)式是严格抛物方程,由文献[1]易知其短时存在性.因此,对于某个ω>0,可以假设,在最大时间区间[0,ω)上方程(0.1)式存在光滑解.

本文中主要考虑h(t),t∈[0,∞)是非负有界光滑函数的情形.为了描述极限超曲面的形状,采用文献[2,6]中的法化方法.对于任意时间t,只要方程(0.1)的解X(·,t)存在,设ψ(t)是一个正因子,使得由

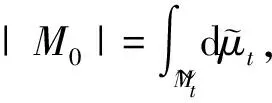

(0.2)

于是得到定理0.1.
定理0.1M0是Rn+1(n≥2)的光滑紧致严格凸浸入超曲面,则在最大时间区间[0,ω)上,发展方程(0.1)式存在唯一光滑解.设平衡项h(t)是非负函数,那么

(Ⅱ)如果0<Λ<∞,则ω=∞,当t→∞时,方程(0.1)式的解C∞-拓扑收敛于球面.
(Ⅲ)如果Λ=0,则ω=∞,当t→∞时,方程(0.1)式的解一致膨胀到∞.而且,如果法化方程(0.2)式的解收敛于光滑超曲面,则极限超曲面必是面积为|M0|的球面.
下面是本文中的主要定理:
定理0.2M0是Rn+1(n≥2)的光滑紧致浸入超曲面,平衡项h(t)是[0,∞)上的非负有界光滑函数,则曲率流(0.1)式的第一类奇异点是渐近自相似的.
定理0.3M0是Rn+1(n≥2)的光滑紧致严格凸浸入超曲面,平衡项h(t)是[0,∞)上的光滑函数,且满足
0≤h(t) (0.3) 设Mn是Rn+1的光滑浸入超曲面.采用文献[4-5]中的记号.特别地,取定Mn的局部坐标系{x1,…,xn},g=gij和A=hij分别表示Mn中的度量和第二基本形式.则平均曲率和第二基本形式的模长平方分别为: H=gijhij,|A|2=gijgklhikhjl, 其中gij是矩阵(gij)的第i行第j列元(i,j)的逆.用λi表示超曲面的第i个主曲率.除非特别说明,本文中的求和表示从指标1到n的求和. 引理1.1对于方程(0.1)式的任意解,下面的发展方程成立: 若M0是凸的,只要曲率流方程(0.1)式的解存在,曲率流就保持所有Mt的凸性,则有下面的引理(或参见文献[2,4,6,10]); 引理1.2(i) 若当t=0时,hij≥0,则对任意t∈[0,ω),都有hij≥0. 由此直接导出关于凸性的结论: |M|和|V|分别表示Mn的面积和Mn包含区域的体积.由引理1.2知道,如果M0是严格凸的,则方程(0.1)式的每个解是紧致凸超曲面.因此,由Aleksandrov-Fenchel不等式和散度定理可以得出|M|与|V|的关系. 设凸超曲面X:Mn→Rn+1的第二基本形式是正定的,其单位外法向量定义Gauss映照v:Mn→Sn,Sn是单位球面.由于超曲面是紧致凸的,即Gauss映照是处处非退化的,则由Gauss映照重新参数化凸超曲面 X=X(v-1(z)),z∈Sn. 定义支持函数 S(z)=〈z,X(v-1(z)〉,z∈Sn. (1.1) 定义凸超曲面X的宽度函数为:ω(z)=S(z)+S(-z),z∈Sn. 下面引用Andrews[11]的一个定理来控制凸超曲面的宽度. 引理1.5Mn是Rn+1的光滑紧致凸超曲面.对任意x∈Mn,若存在正数C1,使得Mn满足逐点Pinching估计λmax(x)≤C1λmin(x),则有ωmax≤C1ωmin, 由此引理,即可得到Sn的内半径和外半径的Pingching估计: 推论1.6Mn是Rn+1的光滑紧致凸超曲面.对任意x∈Mn,若存在正数C1,使得Mn满足逐点Pinching估计λmax(x)≤C1λmin(x).则存在正数C2使得rout≤C2rin. 于是,可以将方程(0.1)式的每个解写成径向图X(x,t)=r(z,t)z:Sn→Rn+1 (1.2) Mt上关于r的外单位法向量和第二基本形式分别为 (2.1) 达种情况下,称曲率流(0.1)式是第一类的.否则,称其为第二类的.下面的引理说明,当t→ω时,任意第一类曲率流一致收敛于爆破点. 引理2.2当t→ω时,方程(0.1)式的解是一致收敛的. 引理2.2的证明根据(2.1)式有 其中C4和C(h)是正数,于是引理得证. 于是,有下面的推论: 定理2.5的证明根据引理1.1的发展方程,有 因此 (2.2) 推论2.6的证明由单调公式,有 因此 根据引理2.3的一致估计,推论得证. 这部分考虑凸曲率流(0.1)式.如果平衡项h(t)足够小,则曲率流(0.1)式收敛于一点,法化曲率流(0.2)式收敛于球面. (3.1) (3.2) (3.3) (3.4) 由推论1.6和(3.4)式得到下面的估计: 下面的引理说明方程(0.1)的解是收缩的,且曲率流的最大存在时间ω有限. 引理3.2ω<∞,当t→ω时,方程(0.1)式的解X(·,t)一致收敛于Rn+1中一点P. 由极大值原理有 H≥φ,0≤t<ω. (3.5) 因此 由此得到(3.5)式. [1] Huisken G, Polden A. Geometric evolution equations for hypersurfaces, calculus of variations and grometric evolution problems[M]∥Lecture Notes in Math(1713). Berlin:Springer,1999,45-84. [2] Huisken G. Flow by mean curvature of convex surfaces into spheres[J]. Differential Geom J,1984,20(1):237-266. [3] Huisken G. Asymptotic behavior for singularities of the mean curvature flow[J]. Differential Geom J,1990,31:285-299. [4] Huisken G. The volume preserving mean curvature flow[J]. Reine Angew Math J,1987,382:35-48. [5] McCoy J. The surface area preserving mean curvature flow[J]. Asian Math J,2003,7(1):7-30. [6] Li G, Salavessa I. Foreed convex mean curvature flow in Euclidean spaces[J]. Manuscripta Math,2008,126:333-351. [7] 吴传喜,喻丽菊,李光汉.由曲率函数和外力场之差支配的凸超曲面的发展[J].数学进展,2010,39(2):233-244. [8] McCoy J. The mixed volune preserving mean curvature flow[J]. Math Z,2004,246(1-2):155-166. [9] Simon L. Lectures on geometric measure theory, proceedings of center for mathematical analysis[M]. Canberra:Australian National University,1983. [10] Zhu X. Lectures on mean curvature flows[M]. AMS/IP Studies in Advanced Mathematice, 32. Providence, RI:American Mathematical Society; Somerville, MA:International Press,2002. [11] Andrews B. Contraction of convex hypersurfaces in Euclidean space[J]. Partial Differential Equations Cale Var,1994,2(2):151-171.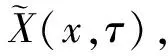
1 预备知识

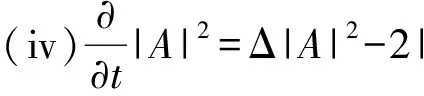
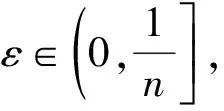

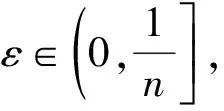

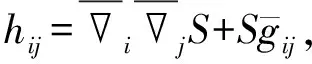
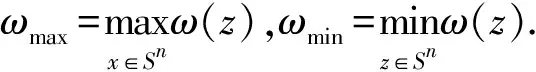
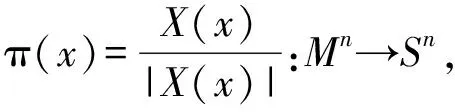
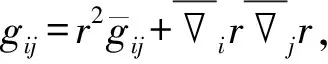
2 自相似解
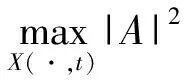

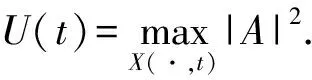


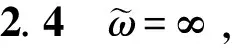
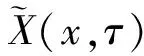
3 收敛于球面