基于二层规划的改进RBF算法在iris数据集分类中的应用

王淑芬 (石河子大学理学院，新疆 石河子 832003)

王 卫 (新疆生产建设兵团化工绿色过程重点实验室(石河子大学)，新疆 石河子 832003)

基于二层规划的改进RBF算法在iris数据集分类中的应用

王淑芬 (石河子大学理学院，新疆 石河子 832003)

王 卫 (新疆生产建设兵团化工绿色过程重点实验室(石河子大学)，新疆 石河子 832003)

基于二层规划上下层相互制约、各自独立决策的性质，融合遗传算法的选择、交叉算子，采用交叉验证方法，动态改善RBF算法的精度，使奇异样本以较大概率落在下层，以得到精度较高的训练网络。研究表明，改进RBF算法可以提高训练网络的泛化能力，并能以较大概率得到预测集中的奇异样本。

二层规划；神经网络；遗传算法；uic数据库；分类

模型精度的优劣是评判模型的重要指标。交叉验证是评价模型精度的常用方法。交叉验证通常有3种，即Hold-Out Method、K-fold Cross Validation和Leave-One-Out Cross Validation，其中K-fold Cross Validation可以有效地避免过学习以及欠学习状态的发生,具有较高的可靠性。笔者结合二层规划上下层相互制约、各自独立决策的性质，在径向基函数神经网络(Radial Basis Function,RBF)模型训练中引入K-fold Cross Validation交叉验证，动态选择训练数据集，使得到的训练模型具有更高的网络泛化能力。

1 二层规划及RBF算法理论简介

1.1二层规划基本理论

二层规划是一种具有二层递阶结构的决策优化问题[1]。上层和下层各有目标函数和约束条件，上层问题的目标函数和约束条件，不仅与上层决策变量有关，而且还依赖于下层问题的最优解或最优值。下层问题的最优解又受上层决策变量的影响，其解(或最优值)反馈到上层而影响上层规划问题的最优解。

1.2RBF算法简介

人工神经网络(Artificial Neural Net- works，ANN)模仿动物神经网络行为特征，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。由于人工神经网络具有非线性适应性信息处理能力，因而在神经专家系统、模式识别、智能控制等领域得到广泛应用[2-5]。常用的ANN模型中，多层感知器神经网络使用反向传播(Error Back Propagation,BP)训练算法，存在收敛速度慢、过多调整参数等问题[6]。径向基函数神经网络(Radial Basis Function,RBF)可以根据具体问题确定相应的网络拓扑结构，具有自学习、自组织、自适应功能，它对非线性连续函数具有一致逼近性，可以进行大范围的数据融合，并行高速地处理数据。目前，RBF神经网络已经成功地用于非线性函数逼近、时间序列分析、数据分类、模式识别、信息处理、图像处理、系统建模、控制和故障诊断等。

2 改进的RBF算法

在RBF网络模型训练中，训练集的选择直接影响训练后网络的精度，导致网络泛化能力较差。通过二层规划模型上下层相互协调，采用遗传算法的自适应、自学习性，动态进行训练集的选择，进而改进算法，提高网络的泛化能力[6]。

2.1改进算法步骤

1)将训练样本随机分为2层，即上层和下层(每层样本个数任意给定，通常上层个数远多于下层个数)。

2)对上层训练样本进行训练。

3)利用上层样本数据进行训练，得到网络对下层样本数据进行测试，观察误差是否达到要求，若达到要求，则输出网络，对测试集进行测试，否则继续进行4)和5)。

4)将上下层样本数据分别代入训练模型，计算上下层样本误差，进行排序。

5)选择上层排序误差较大的n个和下层排序后误差较小的n个样本进行交换，返回2)。

2.2一个奇异样本的算法分析

训练集中存在一个奇异样本情况下，设“输出网络”为事件E，用P(E)表示其概率。假定网络训练中的其余参数已达到最优，只考虑奇异样本对输出网络的影响，若奇异样本不在上层，通过训练能输出理想网络，若奇异样本在上层，通过进行修正使其落到下层以得到理想训练网络。

1)对训练集分层，设训练集样本个数N，上层样本个数为N1,下层样本个数N2(N1+N2=N)。根据奇异样本落在所在层，整个样本被分成2个对立事件，即Ai,i=0,1，Ai表示恰有i个奇异样本分到了上层。

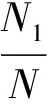
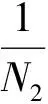
4)奇异样本在A0条件下，得到理想网络的概率为1，即P(E|A0)=1。

2.3多个奇异样本的算法分析

训练集中存在m个奇异样本情况下，设“输出网络”为事件E，用P(E)表示概率。

2)随着奇异样本个数的增加，全部落到下层的概率非常小，即P(A0)为小概率事件。奇异样本在A0条件下，得到理想网络的概率为1，即P(E|A0)=1。

3)在事件Ai,i=1,2,…,m的条件进行网络训练，对上层样本进行修正，此时由于m个奇异样本在上下层的分布具有随机性，如果沿用一个奇异样本的修正策略，会产生很多的无效修正。引入竞争机制，将上下层样本的预测误差排序，既提高了计算效率，同时避免了无效的交叉循环。

4)选择上层排序后误差较大的n个和下层排序后误差较小的n个样本进行交换，经过一定进化代数，得到较好的网络。据实际推断原理，则P(E/Ai) 随着修正次数的增大无限接近1。

综上所述，在训练集存在多个奇异样本的条件下，改进的RBF算法通过竞争机制的引进，不断的调整上下层奇异样本的个数，使上层奇异样本个数逐渐减少，得到较好训练网络的概率P(E)也非常大。

3 实例分析

3.1iris数据集验证

采用uic数据库的iris(鸢尾花)数据集进行算法可行性验证。iris数据集共150个样本，每个样本含4个属性，共分为3类。试验中，在150个原始数据集中随机选择3组数据进行测试，在iris数据集中随机选择3组测试集，每组40个数据，其余110个数据作为训练集使用：

第1组:11，15，19，20，24，26，36，38，42，46，47，50，52，60，63，71，72,73,75,76,79,80,81,82,86,87,98,101,104,114,117,118,119,124,124,128,131,139,142,150。

第2组：7,8,9,15,17,22,23,28,33,35,39,44,47,49,50,62,64,68,73,80,81,93,98,100,102,110,114,117,119,120,125,126,128,129,133,135,137,142,144,150。

第3组:1，4，6，8，9，11，16，17，18，21，28，30，32，33，38，40，41，44，49，50，70，73，75，77，78，80，83，84，88，98，101，103，115，123，124，126，127，133，134，145。

表1 RBF算法和改进RBF算法准确率比较

对1组测试集随机进行100、200和500次预测，结果如表1所示。从表1可以看出，改进RBF算法比原有算法的准确率高，说明改进的RBF算法能提高测试集预测精度。

3.2对iris预测集结果统计分析奇异样本

分别对iris数据集随机选择的上述3组测试集各进行500次试验，如图1所示。从图中可以看出，第1组数据中序号为18、33、38的样本预测结果较差，第2组数据中序号为29、30、36的样本预测结果较差，第3组数据中序号为22、25、28的样本预测结果较差。

图1 数据500次测试各样本误差次数

第1组的18号与第3组的22号同为原始数据的73号样本。第1组的33号和第2组的29号同为原始数据的119号样本。3组数据的随机分类包含了85个不同的原始数据，在每组进行500次试验中，原始数据的73号样本和119号样本出错的次数较多，说明150个原始样本数据中73号和119号成为奇异样本的概率很大。

4 结 语

根据二层规划各层变量独立决策、相互影响的性质并融合遗传算法的遗传算子，提出动态选择训练集的改进RBF算法。通过iris数据集的验证表明，改进的RBF算法能获得优良的训练网络，从而提高预测的准确率。大量随机试验结果显示，某些样本误差出现的次数非常高，为奇异样本的概率很大。因上，上述研究对疾病诊断、生物制药、基因变异等相关领域的研究会起到积极作用。

[1]滕春贤,李智慧.二层规划的理论与应用[M].科学出版社,2002.

[2]鲍鸿,黄心汉,李锡雄.广义模糊推理与广义模糊RBF神经网络[J].控制与决策,2000,15(2):205-208.

[3]薛富强,葛临东,王彬.基于改进递阶遗传算法的RBF神经网络分类器[J].系统仿真学报,2010(2):399-402.

[4]叶健,葛林东,吴月娴.一种优化的RBF神经网络在调制识别中的应用[J].自动化学报,2007,33(6):652-654.

[5]梁斌梅,韦琳娜.改进的径向基函数神经网络模型预测[J].计算机仿真,2009,26(11):191-194.

[6]李杰,韩正之.一种估计人工神经网络泛化误差的新方法[J].控制理论与应用，2001,18(2): 257-259.

10.3969/j.issn.1673-1409(N).2012.08.044

TP274

A

1673-1409(2012)08-N134-03

2012-05-12

新疆生产建设兵团博士基金项目(2011BB011)。

王淑芬(1979-)，女，2002年大学毕业，硕士，讲师，现主要从事遗传算法、神经网络理论及应用方面的教学与研究工作。

[编辑] 李启栋