J-右(左)酉矩阵的性质与分解
2012-11-21贺阳
贺 阳
(韩山师范学院数学与应用数学系,广东潮州 521041)
1 引言与预备知识
本文所用的符号和所引用的结论均取自文献[1-6],用Cn×n表示复数域上n阶方阵的全体;用Rn×n表示实数域上的n阶方阵的全体;用In表示n阶单位矩阵;用Jn表示n阶次单位矩阵即次对角线上的元素都为1其余各位置的元素都为0的n阶矩阵;记2n阶矩阵用AL、AR、AT、AH、AST、ASH、det A分别表示复数矩阵A的左转置矩阵、右转置矩阵、转置矩阵、共轭转置矩阵、次转置矩阵、次共轭转置矩阵及行列式;如无特别说明,本文所提的数均为复数域上的数,本文所提的矩阵均为复数域上的矩阵.
定义1 设A∈C2n×2n,若A满足:AAL=ALA=J(其中AL=JAH),则称A为J-左酉矩阵.若A满足:AAR=ARA=J(其中AR=AHJ),则称A为J-右酉矩阵容易看出,若A为J-右(左)酉矩阵,则A为可逆矩阵;JA=AJ;且J,I为J-右(左)酉矩阵.
引理1[2]设A∈C2n×2n,则A=QR(Q R分解),其中Q为2n阶酉矩阵,R为2n阶与矩阵A秩相同的矩阵.
引理2[2]设 A∈C2n×2n,则 A=UΛV(奇异值分解),其中U,V为酉矩阵,Λ=diag( )λ1,λ2,…,λ2n,其中 λ1≥λ2≥…λ2n≥0 , λ1,λ2,…,λ2n为A的特征值.
性质1 设A∈C2n×2n,且A为J-右(左)酉矩阵,其中B,C为n阶矩阵.
性质2 设A∈C2n×2n,且 A为J-右(左)酉矩阵,则为n阶矩阵,则B,C满足如下条件:BJnBH+CJnCH=0,BCH+CBH=In,BHB+JnCHCJn=0,BHC+JnCHBJn=In.
证明 由J-右酉矩阵的定义直接计算可得.
这 里 设 Λ1=diag(λ1,λ2,…,λn) 其 中 λ1,λ2,…,λn为 B 的 特 征 值 , 且 λ1≥λ2≥…λn≥0,Λ2=diag(,,…,)其中,…为C的特征值,且≥≥…≥0.
2 J-右(左)酉矩阵的性质
定理1 设A∈C2n×2n,则以下三个命题等价.
(1) A为J-右酉矩阵;
(2) A为J-左酉矩阵;
(3) A为酉矩阵,且JA=AJ;
证明 (1)⇒(2)若 A为 J-右酉矩阵,得 AAHJ=AHJA=J,且 JA=AJ,则 AAH=AHA=I,JAHA=JAAH=AJAH=J,则A也为J-右酉矩阵.
(2)⇒(3)若A为J-左酉矩阵,则JAHA=AJAH=J,且JA=AJ,则AAH=AHA=I,即A为酉矩阵.
(3)⇒(1)AAH=AHA=I,且JA=AJ,则JAAH=AJAH=J,AHAJ=AHJA=J,即 A为J-右酉矩阵.
由定理1可得A为J-右酉矩阵,则A也为J-左酉矩阵的情况类似,所以A在J-右酉矩阵上所得的定理在J-左酉矩阵上也有相关定理,因此下文只介绍J-右酉矩阵的定理,J-左酉矩阵的定理用同样的方法即可推出.
定理2 设A为J-右酉矩阵,则有以下结论成立
(1) A,AJ均为酉矩阵.
(2) A-1,AH,ASH均与J满足交换律.
(3) AL,AR,AT,AST仍为J-右酉矩阵.
证明 (1)由 AAR=AAHJ=J,则 AAH=I,同理 ARA=AHJA=AHAJ=J,得 AHA=I,则 A为酉矩阵.AJ的证明方法类似.
(2) A为J-右酉矩阵,则AJ=JA,且A为可逆矩阵,则A-1J=JA-1.AH、ASH的证明方法类似.
(3) A为J-右酉矩阵,且AL=JAH,则AL(AL)R=JAHA=(AL)RAL=AJAH=J,则AL为J-右酉矩阵.AR、AT、AST的证明方法类似.
定理3 设A,B均为J-右酉矩阵,则BA-1、BAHB、BASHB均为J-右酉矩阵.
BAHB、BASHB的证明方法类似.
定理4 设A1,A2,A3,…,Am均为J-右酉矩阵,且A1,A2…An为n阶矩阵,n1,n2,…nm为正整数,则为J-右酉矩阵.
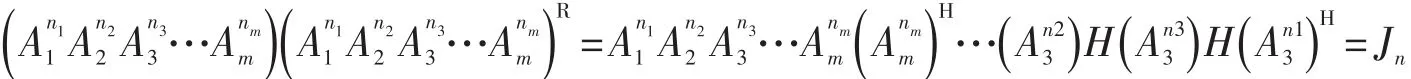
3 J=右(左)酉矩阵的分解
定理5 设A∈C2n×2n,且A为J-右酉矩阵,则且B为不可逆矩阵,C为可逆矩阵,若C=V2Λ2U2(其中U2,V2为n阶酉矩阵)则存在矩阵使得A=D01D02D03D04或存在矩阵使得 A=D05D06D07D08.
定理6 设A∈C2n×2n,且 A为J-右酉矩阵,则,且B为可逆矩阵,C为不可逆矩阵,若B=V1Λ1U1(其中U1,V1为n阶酉矩阵)则存在矩阵使 得 A=D11D12D13D14或 存 在 矩 阵使得 A=D D D D.15161718
证明方法与定理5类似,不再证明.
致谢感谢韩山师范学院刘玉教授的悉心指导!
[1]刘玉,蔡增烁.全酉矩阵及其性质[J].韩山师范学院学报,2009,30(6):1-3.
[2]戴华.矩阵论[M].北京:科学出版社,2001:131-132,140-141.
[3]袁晖坪,王行荣,李庆玉.行(列)反对称矩阵的满秩分解和广义逆[J].数学杂志,2009,29(4):515-516.
[4]黄允发.K-可逆矩阵与K-可换矩阵[J].韩山师范学院学报,2009,30(6):21-25.
[5]刘玉,蔡乌芳,郑则礼.K-次对称矩阵及其性质[J].南通大学学报:自然科学版,2010,2(9):86-87.
[6]许永平,石小平.正交矩阵的充要条件与O-正交矩阵的性质[J].南京林业大学学报:自然科学版,2005,29(2):54-56.
