交通网络最优抗堵塞路径的选择模型与计算
2012-11-21葛长飞
葛长飞
(盐城师范学院商学院,江苏 盐城 224051)
交通网络最优抗堵塞路径的选择模型与计算
葛长飞
(盐城师范学院商学院,江苏 盐城 224051)
从交通网络堵塞后替代路径与原最短路径之间关系出发,提出交通网络的最优抗堵塞路径选择模型,设计了最优抗堵塞路径选择模型的算法,对算法的复杂性进行了分析,并以盐城市实际局部路网为例进行了验证,得出该区域的最优抗堵塞路径。
交通网络;抗堵塞路径;算法
随着社会经济发展和汽车销售量不断增长,居民或者运输车辆在行驶过程中,经常遇到交通道路堵塞的情况,且这种堵塞在短时间是无法恢复。由于交通网络中2点对之间存在多条路径,且每条路径上任意路段都可能堵塞,因此如何选择一条尽可能降低由于堵塞带来的损失,显得尤为重要。
在以往对交通堵塞的研究工作中,主要有以下几个方面:一是对最短路径上和最长绕行关键边的研究[1-2];二是对不完全信息下实时关键边和关键路径的研究[3-4];三是对交通网络抗堵塞能力的研究[5]。但缺乏从抗堵塞能力角度对交通网络网中任意点对间路径选择的研究。为此,笔者提出了一种最优抗堵塞路径选择模型。
1 最优抗堵塞路径选择模型
给定G(V,E),V={v1,v2,…,vn}为G(V,E)的节点集合,E为G(V,E)的集合。若s为出发节点,t为最终节点,则w(eij)为eij的权重。σk={pg(s,t)}为s到t的k条路径的集合,dg(s,t)为pg(s,t)路径的长度,假设交通网络中只发生一次堵塞,且堵塞的位置和时间未知,居民和车辆应当如何选择路径使得损失最小化。
定义1任意一条I路径上抗堵塞系数:

定义2最优抗堵塞路径为:
从定义2可知,计算出每条路径的抗堵塞能力的最大值后,最优抗堵塞路径就转化为最小最大的问题。即交通网络中某条路径出现堵塞后存在最短路径与原最短路径的最差替代效果,与其他路径的堵塞后最短路径和原最短路径最差替代效果进行比较,最小值就是最优的抗堵塞路径。
2 最优抗堵塞路径算法与算法复杂性分析
2.1最优抗堵塞路径算法
步1 对于路径pI(s,t)中起止点vs,利用Dijkstra标号法计算vs计算出到任一节点vsu最短路径长度dIp(s,su),遍历u=1,2,…,d(s),其中,d(s)为节点vs的度数。
步2 去掉与vs相关联边es,su,再次使用利用Dijkstra标号法计算vs计算出到节点vsu的最短路径长度dIp-es,su(s,su),即可以计算出所有的dIp-es,su(s,t),其中,d(s)是vs的度数。
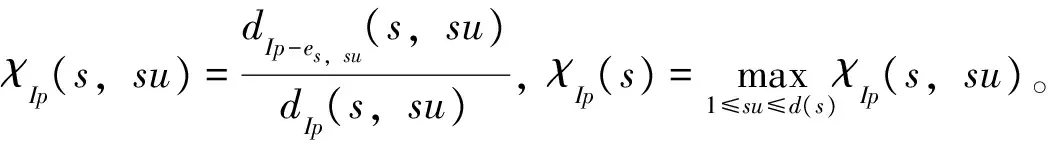

步5 重复步1到步4,计算出所有k条路径的(χ1p,χ2p,…,χkp)。
2.2算法复杂性分析
对于顶点为n的网络图,k为(s,t)的路径的条数,最优抗堵塞路径算法的算法复杂性如下:步1的计算次数为O(n2);步2的计算次数为O(n2)*d(s);步3的计算次数为O(d(s));步4的计算次数为O(n4);步5的计算次数为k*O(n4) ;步6的计算次数为O(k)。

3 实例分析

图1 盐城市局部交通网络抽象
以江苏省盐城市实际交通网络为例,进行最优抗堵塞路径选择。首先将盐城市局部地图抽象成交通网络图(见图1)。假设v1为出发节点,v6为目标节点。
利用上述算法进行最优抗堵塞路径的选择。由图1可知点对间(v1,v6)最短路径有3条:
路径1:v1→v2→v3→v6;路径2:v1→v2→v5→v6;路径3:v1→v4→v5→v6。
通过以上分析可知,以v1为出发节点、v6为目标节点的3条路径中,交通网络中路径2出现堵塞后存在最短路径与原最短路径的最差的替代效果,比其他路径1和路径3的堵塞后最短路径和原最短路径最差替代效果要好,则路径2就是最优的抗堵塞路径。
[1]苏兵,肖鹏.交通网络最优安全路径选择模型与算法[J].西安交通大学学报,2008,42(4):395-398.
[2]刘明.不完全信息下交通网络的关键路径选择问题[J].系统工程,2006,24(12):17-20.
[3]苏兵.连接网络上的占线的可恢复加拿大旅行者问题[J].系统工程理论与实践,2009,25(2):108-113.
[4]Corley H W,Asakura Y,Kashiwadani M.Road network reliability caused by daily fluctuation of traffic flow[A].Proceedings of the 19thPTRC summer annual Meeting Brighton[C].University of Brighton,2011:73-84.
[5]苏兵,徐寅峰.交通网络的抗堵塞能力分析与计算[J].系统工程,2005,23(6):16-20.
[编辑] 洪云飞
10.3969/j.issn.1673-1409(N).2012.12.035
TB114.1
A
1673-1409(2012)12-N108-02
