遗传算法在最小Steiner树问题中的应用研究

陈智豪,杨天明

(江苏农林职业技术学院基础部，江苏 句容 212400)

遗传算法在最小Steiner树问题中的应用研究

陈智豪,杨天明

(江苏农林职业技术学院基础部，江苏 句容 212400)

简单介绍了最小生成树和最小Steiner生成树的概念，通过实例(有线通讯网络问题)提出了一种求解最小Steiner生成树问题的遗传算法。试验结果表明，该算法能够收敛到全局近似最优解。

遗传算法；最小生成树；最小Steiner生成树

进化计算是人工智能(AI)领域的一种方法，它包括4种典型的计算方法。其中，遗传算法(GA)相对来说比较成熟，是目前得到广泛应用的方法。遗传算法是一种模拟达尔文的自然选择、自然淘汰、适者生存的生物进化过程的计算模型，通常实现方式是通过计算机来模拟遗传的过程，常常用于在计算数学学科中解决最优化问题的搜索[1]。下面，笔者利用遗传算法求解最小Steiner生成树问题，从而利用该解法解决有线通讯网络的布线问题。

1 最小生成树和最小Steiner生成树

在一个赋权连通图G=(V,E)中，如果存在子图G′包含G中所有顶点和一部分边，且不形成回路，则称G′为图G的生成树。其中，权值最小的生成树则称为最小生成树。用于求解最小生成树的算法之中最著名的也是最经典的就是Prim算法和Kruskal算法。如果除了已知的顶点之外还能够添加一些点，那么就能得到多个最小生成树了。而在所有最小生成树中总权值最小的树就是最小Steiner生成树。增加的点则称为Steiner点[1]。

结论1对于n个给定的点v1,v2,…,vn,最小Steiner生成树T*总是存在的。

结论2对于n个给定的点v1,v2,…,vn,设最小Steiner生成树T*中Steiner点的个数为s，则s≤n-2。

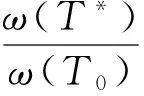
结论4已知平面上n个点为P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)，设：

xu=max{x1,x2,…,xn)xd=min{x1,x2,…,xn}

yu=max{y1,y2,…,yn}yd=min{y1,y2,…,yn}

那么所有Steiner点都必定包含在点集{(x,y)|xd≤x≤xu,yd≤y≤yu}之内。

以上4个结论表明：①最小Steiner生成树存在；②Steiner点的个数不超过给定点个数减去2；③利用最小Steiner生成树设计出的路线和最小生成树相比较最多能够缩短大约13.4%；④可以确定Steiner点的坐标取值范围。

2 应 用

2.1 有线通讯网络问题

设给定位于同一水平面上的16个通讯站，要在这些地点之间铺设光缆，使得费用最少。每个地点作为图G=(V,E)的一个顶点，顶点集V={P1,P2,…,P16}，地点的坐标见表1。

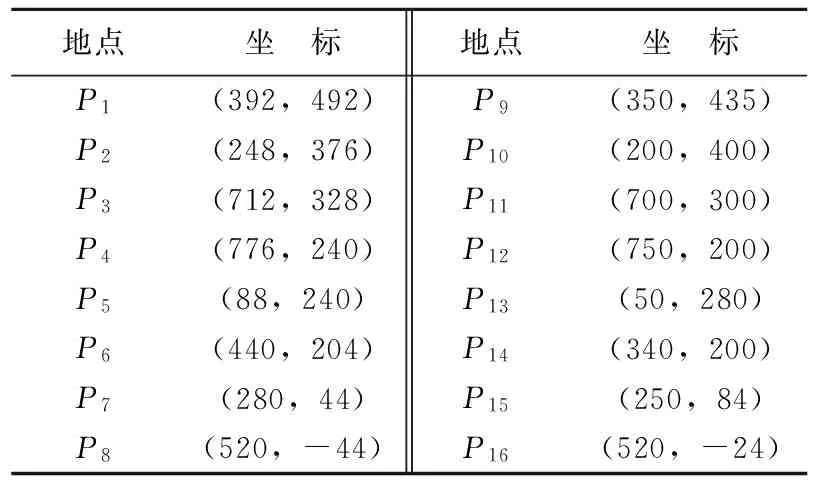
表1 各地点的坐标 (单位：m)

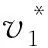
2.2 算法设计

遗传算法是求解最小Steiner生成树问题的一种近似解法，它是由染色体编码方法、个体适应度评价、遗传算子、运行参数共4个主要的要素构成的。

1)编码与解码 采用二进制编码，也就是用由0和1这2个数字构成的字符串表示所有的个体，一个个体对应着一组待求的点。为了把搜索范围限定在矩形框内，就要把矩形区域放缩到[0,1]×[0,1]的单位面积正方形，相应的每个点的坐标也要进行放缩。每个个体的二进制编码结构如下：

其中，*是0或1。

一个个体是随机生成的一个二进制字符串，长度是ws=ds×p。其中,ds是待求的Steiner点的个数，在运行程序时自己设定。p是一个待求点对应的二进制编码长度，如果要求精确到小数点后第k位，则p=dx+dy，其中dx=[log2(10k×cx)]，dy=[log2(10k×cy)]。

对于一个个体的解码，首先需要根据个体结构将个体的编码分段，然后把每一段编码转换为十进制数字：

再把这些十进制的数字转换为点的坐标(x1,y1),(x2,y2),…,(xds,yds)：

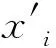
这样就可以把用二进制编码表示的个体解码得到所有待求点的坐标了。

2)初始群体的选取 设种群规模为M，那么就根据要求的计算精度，随机产生M个介于0和1之间用二进制码表示的字符串，构造出初始种群。这M个互不重复的二进制字符串就形成了一个一个的个体。每个个体可以根据编码与解码中的办法解码得到待求点的坐标。

3)对种子的评价 对于某个个体所对应的生成树，要判断其优劣主要是看其目标函数值。取以已知点和待求点作为顶点的图的最小生成树长度作为目标函数值。这个值当然是越小越好。

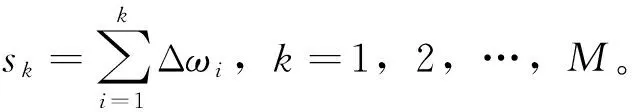
接着，在[0,1]区间上随机地产生M个数r。如果r落在第m个小区间内，则选择保留与之对应的那个个体。这目标函数值越小则对应的小区间越短，在轮盘上占据的范围就越小，那么该个体比较不容易被选中；反之，则更容易被选中。把这一步骤反复进行多次之后，适应度较高的个体将会有较大的可能被选中从而保留下来。

5)交叉 笔者采用是单点交叉操作，交叉点是随机生成的，交叉概率pc=0.03。在执行交叉操作时，2个父代个体通过在随机产生的交叉位处互换字符串的方式进行交叉。再把交叉产生的子代个体全部放入群体中，而执行过交叉操作的父代则舍弃。

6)变异 笔者采用单点变异操作[3]，变异概率为0.03。变异的基因位是随机生成的，把要执行变异操作的基因位上的数0变成1或1变成0。

2.3 试验

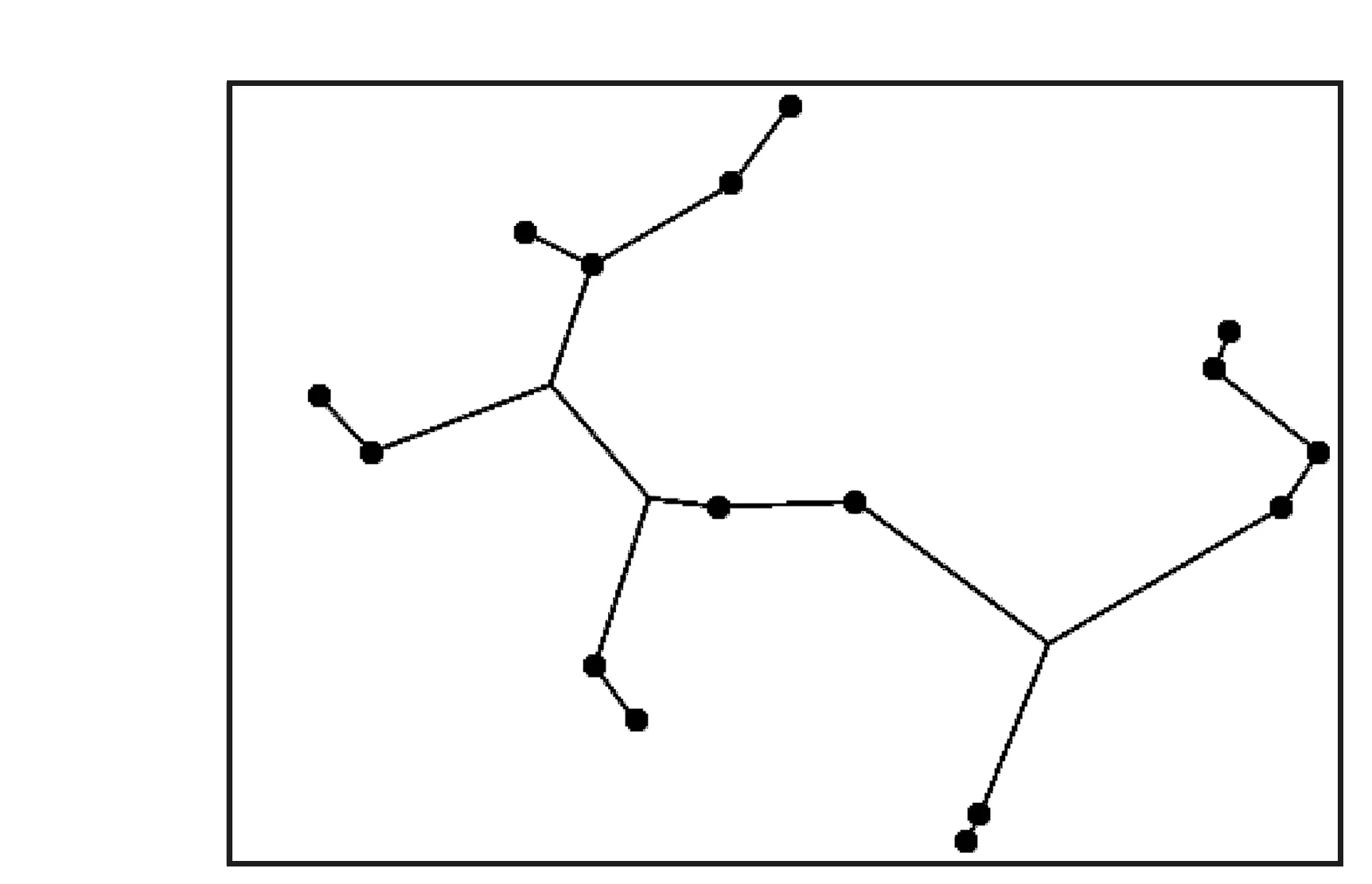
图1 最小Steiner生成树图形

上述算法通过Mathematics7.0编程，在Windows7系统中运行通过。对于给出的上述16个站点，笔者经过多次试验发现，当Steiner点的个数取为ds=3个时效果最好。利用笔者提出的解法随机求解10次，算法迭代平均10次左右即可收敛到近似最优解，得到的最小Steiner生成树的最优近似解为1651.854，和最小生成树的结果1704.7相比较而言，总路径长度缩短了3.1%。Steiner点的坐标分别是(217.961,289.078),(289.577,206.626),(579.942,100.617)。最小Steiner生成树的图形如图1所示。

[1]雷英杰.Matlab遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2005.

[2]Du D Z，Hwang F K.A Proof of the Gilbert-Pollak conjecture on Steiner ratio[J].Algorithmica，1992(7):121-135.

[3]马良，蒋馥.度限制最小树的蚂蚁算法[J].系统工程学报,1999,14(3):211-214 .

[编辑] 洪云飞

10.3969/j.issn.1673-1409(N).2012.10.005

O242.2

A

1673-1409(2012)10-N013-02