利用组合理论计算独立同分布随机变量和的高阶矩
2012-11-20左路
左 路
(湖北大学化学化工学院,湖北 武汉 430062)
利用组合理论计算独立同分布随机变量和的高阶矩
左 路
(湖北大学化学化工学院,湖北 武汉 430062)
中心极限定理建立了关于独立同分布的随机变量和的极限分布,但是并未给出随机变量和的高阶矩的计算方法。将利用组合理论建立独立同分布且均值为零的随机变量序列和的高阶矩的简化计算方法,并在该方法的基础上扩展至一般独立同分布随机变量序列和的高阶矩。
中心极限定理;组合理论;高阶矩
对于一般的非中心化独立同分布随机变量序列,虽然根据中心极限定理,其和的极限分布为正态分布,但是计算和的高阶矩即使在正态分布环境下仍然很复杂。在独立性、中心化的环境下,利用随机变量和的幂运算展开式中变量排列表现出来的组合性质,容易构建随机变量和的高阶矩的简化计算公式,并可以在此基础上推广至一般非中心化独立同分布的随机变量序列。
1 中心化随机变量序列和的高阶矩
定理1设{Xi,i∈N}为独立同分布随机变量序列,存在:
E(Xi)=0 0 其中下标r(1),…,r(n)为从元素1,…,N中允许重复取得的n个元素。如当N=8,n=6时: 记φπ=φ(Xr(1)…Xr(n)),则式(1)可表达为: (2) (3) 于是: (4) (5) 根据q和n的关系从3个方面讨论式(5): (6) (7) 式(7)中的求和项数为所有双元素划分π的数量为(n-1)(n-3)…5·3·1。 当n为奇数时,由于划分π中的块不可能都为双元素块,至少有一个单元素块,因此φπ=0。 综上所述,有: (8) 定理2设{Yi,i∈N}为独立同分布随机变量序列,存在: E(Yi)=μ0 [1]苏淳. 概率论[M]. 第2版.北京:科学出版社,2010. [2] Emery M, Nemirovski A,Voiculescu D. Lectures on probability theory and statistics[M].New York:Springer, 2000. [编辑] 洪云飞 10.3969/j.issn.1673-1409(N).2012.10.004 O211.4 A 1673-1409(2012)10-N010-03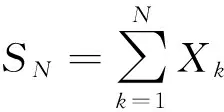
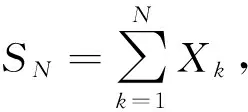
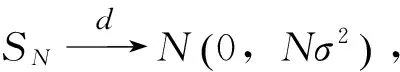
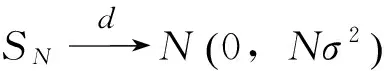
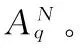
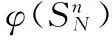

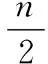
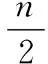
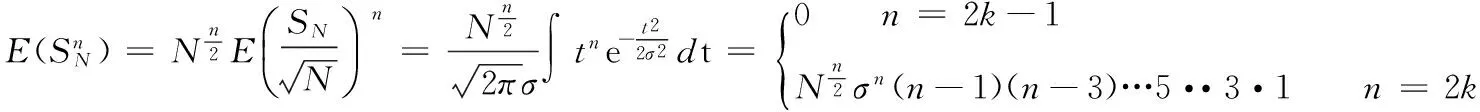
2 非中心化随机变量序列和的高阶矩