五种常规三轴强度准则的比较*
2012-11-17付义胜
付义胜
(河南理工大学能源科学与工程学院, 河南焦作市 454010)
五种常规三轴强度准则的比较*
付义胜
(河南理工大学能源科学与工程学院, 河南焦作市 454010)
基于6种岩石的试验数据对5种常规三轴强度准则进行拟合。以拟合偏差绝对值之和最小为目标确定强度准则中待定参数,进而比较拟合偏差以及单轴抗压强度σC和抗拉强度T的预测值与试验值差异。研究发现:含有3个参数的广义Hoek-Brown准则、指数强度准则和ROCKER准则预测的单轴抗压强度与试验值基本一致;ROCKER
准则预测的单轴抗拉强度与试验值较接近;广义Hoek-Brown准则具有较小的拟合偏差,抗拉强度对强度准则的拟合结果没有明显影响。
常规三轴强度准则;Mohr-Coulomb强度准则;Hoek-Brown准则;指数强度准则;ROCKER准则
岩石常规三轴强度准则一般写为:

式中,σ1,σ3分别为最大和最小主应力,以压应力为正。尤明庆[1-2]、石祥超等[3]比较了几种强度准则的拟合精度,但并未考虑强度准则对抗拉强度的预测能力。Ghazvinian等[4]研究了有无抗拉强度数据对强度准则预测单轴抗压强度的影响,但岩石材料与强度准则的选用都比较单一。Carter等[5]研究岩石强度准则时强制拟合曲线通过抗拉强度数据点,导致其拟合曲线明显偏离多数试验数据点。本文基于6种岩石的试验数据对5种常规三轴强度准则进行拟合,以拟合偏差绝对值之和最小为目标确定强度准则中待定参数,比较平均拟合偏差mf以及强度准则所预测的岩石单轴抗压强度和单轴抗拉强度与试验值的关系。
1 岩石的几种常规三轴强度准则
1.1 Mohr-Coulomb强度准则
Mohr-Coulomb强度准则(简称M-C准则)是岩体力学中经典强度理论:

式中,τ为剪切力,σn为破坏面上正应力;c和φ分别是岩石材料的粘聚力和内摩擦角。
M-C准则还可以写为主应力的形式:

式中,m为相关参数;σC为岩石试样的单轴抗压强度。m和σC可用粘聚力和内摩擦角表示:
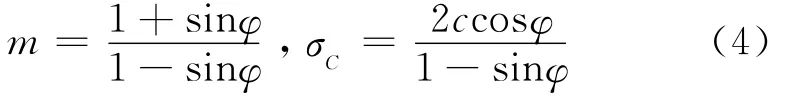
单轴抗拉强度T和拟合曲线在σ3=0的斜率K0分别由下式计算得出[2]:
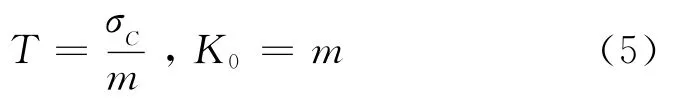
Mohr-Coulomb强度准则形式简洁具体,具有明确的物理背景,广泛应用于岩体工程的设计和地质构造方面的分析[6]。
1.2 H-B准则及GH-B准则
Hoek-Brown强度准则(简称H-B准则)[7]:
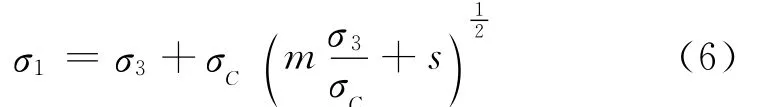
式中,σ1,σ3分别为岩体破坏时的最大和最小主应力;m、s为相关参数。完整岩块,取s=1。
单轴抗拉强度T和K0分别由下式得出[2]:
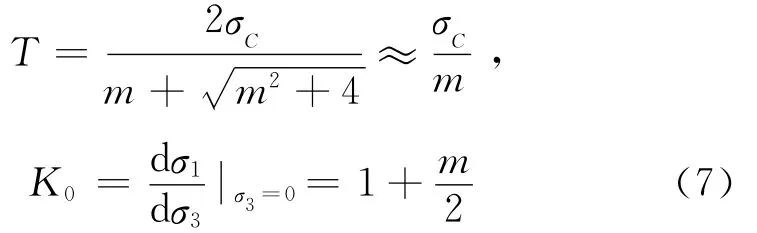
后修正为[8]:

式(8)又称为广义Hoek-Brown强度准则(简称GH-B)。完整岩块,取s=1,式(8)可化简为:

单轴抗拉强度T和K0为[2]:
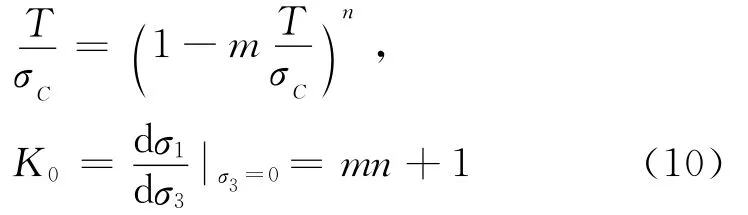
1.3 指数强度准则
M.You[9]构造出含有3个岩石材料参数的指数强度准则(简称EXP准则):
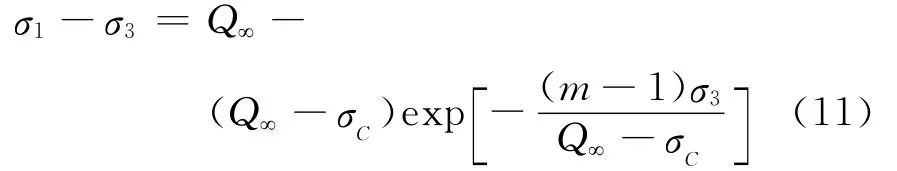
式中,Q∞为极限主应力差;σC为岩石试样的单轴抗压强度;m为相关参数。
将σ1=0,σ3=-T代入上式可求得抗拉强度,而K0可由下式得出[2]:
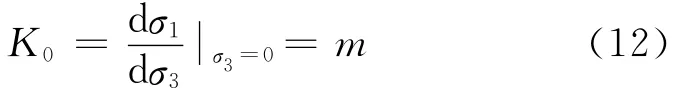
1.4 ROCKER强度准则
ROCKER强度准则(简称Rock准则)是由B.J.Carter等[5]提出的,其表达式为:
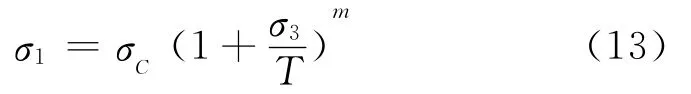
式中,T为岩石的单轴抗拉强度,为正值;σC为岩石的单轴抗压强度;指数m取值范围为0.3~1。
K0可由下式得出:

2 试验数据及拟合方式
用于评价强度准则的岩石的试验数据从文献中引用。Tyndall石灰岩(TL)和Lac du Bonnet花岗岩(LG)的试验数据引自于文献[5];Mesaverde第3组页岩垂直层理(S⊥)和平行层理(S∥)、第5组砂岩垂直层理(SS⊥)和平行层理(SS∥)的试验数据引自文献[10]。同一围压下有两组试验数据时拟合中取平均值。岩石试验数据的特征见表1。由于岩石的巴西劈裂强度与单轴拉伸强度都有较大离散性,两者平均值大致相当[11],故下面不做区分。
本文采用偏差绝对值之和达到最小而不是常用的最小二乘法来确定拟合参数,拟合曲线能靠近大量的正常试验点,并使异常点具有较大的偏差[1-2]。
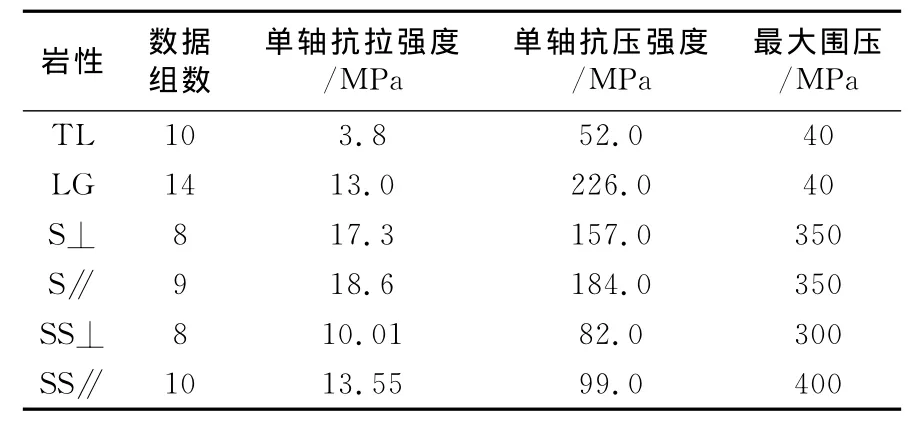
表1 岩石试验数据的特征
3 强度准则的比较与分析
3.1 Tyndall石灰岩
含3个参数的GH-B准则、EXP准则和ROCK准则对Tyndall石灰岩单轴抗压强度的预测值与试验值均为52MPa,但含2个参数的M-C准则和HB准则的预测结果分别比试验值偏高近40.4%和14.4%(见表2)。ROCK准则对单轴抗拉强度的预测值为3.5MPa,接近于试验值3.8MPa,其他4种强度准则的预测结果与试验值互有高低,差异较大。有抗拉强度和无抗拉强度数据参与拟合对强度准则预测单轴抗压强度和抗压强度的影响很小。M-C准则的平均拟合偏差mf最大,GH-B准则的相对最小。
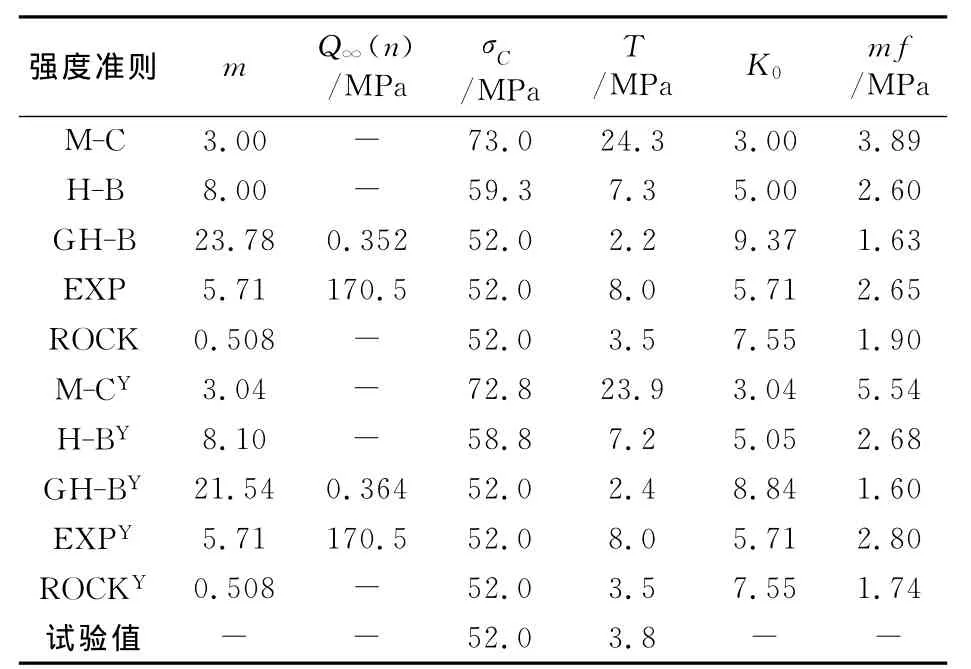
表2 Tyndall石灰岩的拟合结果
图1为Tyndall石灰岩无抗拉强度数据的强度准则拟合曲线,因有抗拉强度数据的拟合曲线与其差别不大,故下面均不再给出。直线型的M-C准则在低围压区域内,拟合曲线偏离单轴抗压强度和抗拉强度的试验数据点。GH-B准则的K0值相对最大,其对单轴抗拉强度的预测值比试验值显著偏低。ROCK准则的拟合曲线通过大多数试验数据点,拟合效果较理想。

图1 Tyndall石灰岩的强度准则拟合曲线
3.2 Lac du Bonnet花岗岩
M-C准则对Lac du Bonnet花岗岩单轴抗压强度的预测值比试验值偏高近17.8%,其他4种强度准则的预测值与试验值226MPa基本一致(见表3)。EXP准则对单轴抗拉强度的预测值为11.8 MPa,较接近试验值13.0MPa,M-C准则的预测结果是试验值的近2倍,其他3种准则的预测值仅是试验值的一半甚至更低。M-C准则的平均拟合偏差mf依然最大,GH-B准则和ROCK准则的相近。有抗拉强度和无抗拉强度数据参与拟合对拟合的结果影响很小,甚至没有影响,如M-C准则和H-B准则。
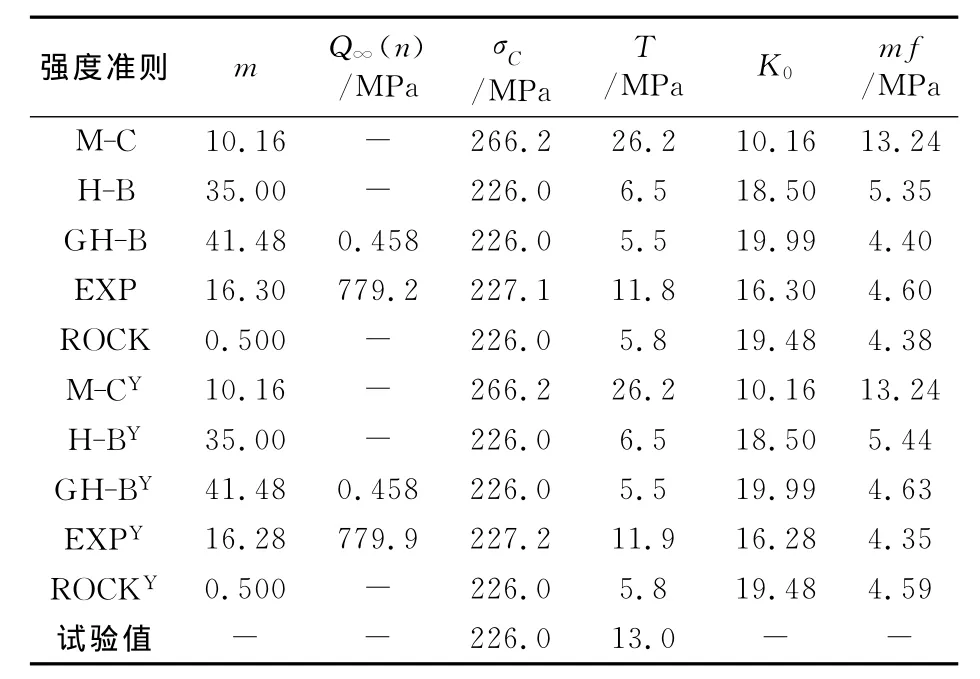
表3 Lac du Bonnet花岗岩的拟合结果
从图2中可看出,M-C准则的拟合曲线依然偏离单轴抗压强度和抗拉强度的数据点。H-B准则、GH-B准则和ROCK准则的K0值接近,其拟合曲线基本重合。EXP准则的拟合曲线较接近抗拉强度数据点,也大致通过其他试验数据点,整体拟合效果较好。
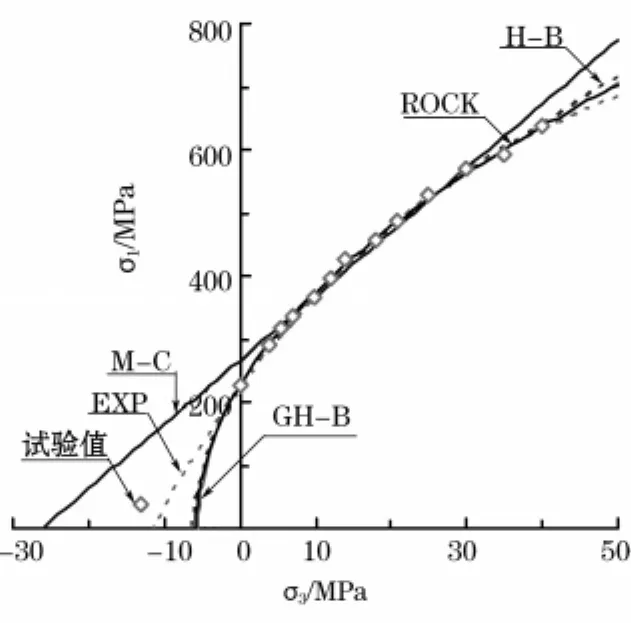
图2 Lac du Bonnet花岗岩的强度准则拟合曲线
3.3 Mesaverde页岩
Mesaverde页岩有抗拉强度和无抗拉强度数据对拟合结果影响很小,这与以上Tyndall石灰岩和Lac du Bonnet花岗岩的情形类似,故下面不再给出有抗拉强度数据的拟合结果。
GH-B准则、EXP准则和Rock准则对Mesaverde页岩单轴抗压强度的预测值与试验值基本一致。H-B准则对S⊥单轴抗压强度的预测值与试验值一致,其对S∥的预测值比试验值偏高5.9%。这5种强度准则对S⊥单轴抗拉强度的预测值与试验值差异较大,ROCK准则的平均拟合偏差最小(见表4、表5)。GH-B准则对S∥单轴抗拉强度的预测结果为17.6MPa,接近于试验值18.6MPa,其平均拟合偏差mf最小。
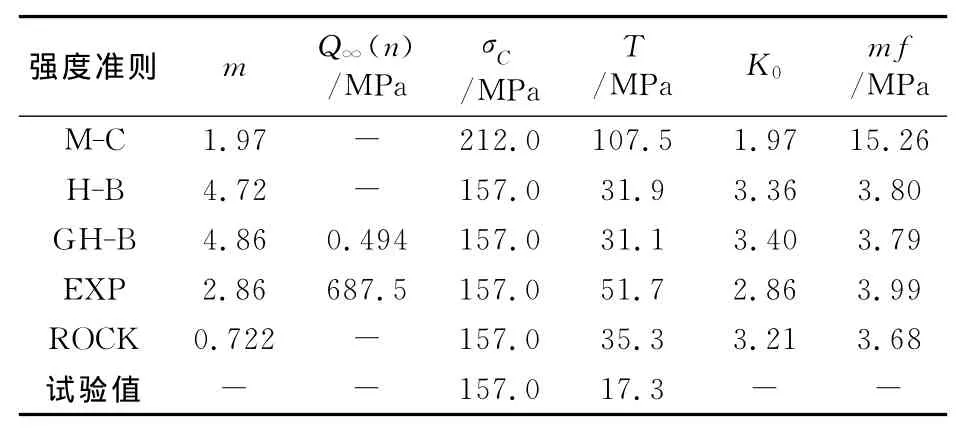
表4 Mesaverde页岩垂直层理的拟合结果
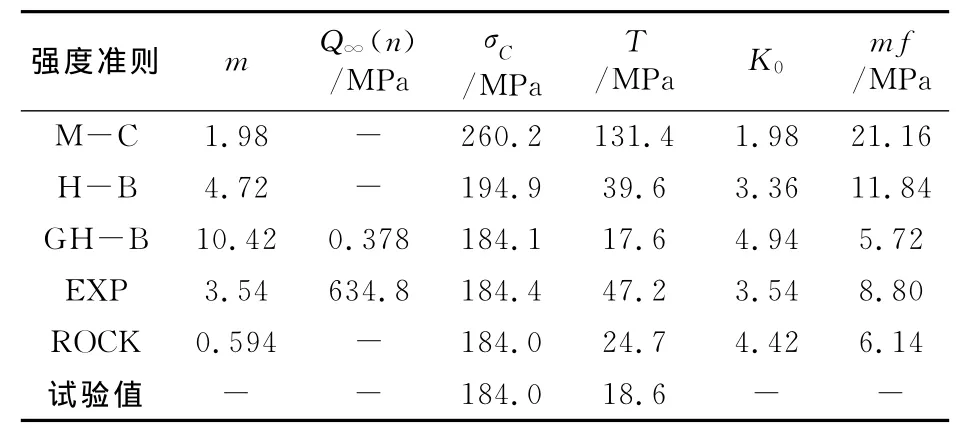
表5 Mesaverde页岩平行层理的拟合结果
5种强度准则的拟合曲线均偏离抗拉强度的数据点(见图3、图4)。ROCK准则的拟合曲线通过S⊥大多数试验数据点,而GH-B准则拟合曲线通过S∥大多数试验数据点。
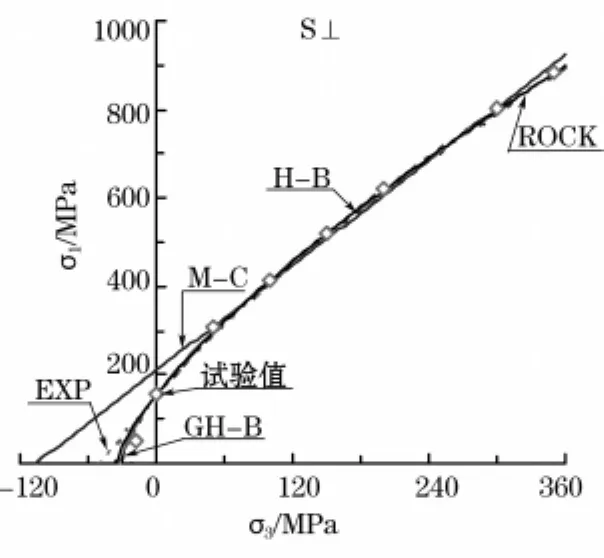
图3 砂岩垂直层理的强度准则拟合曲线
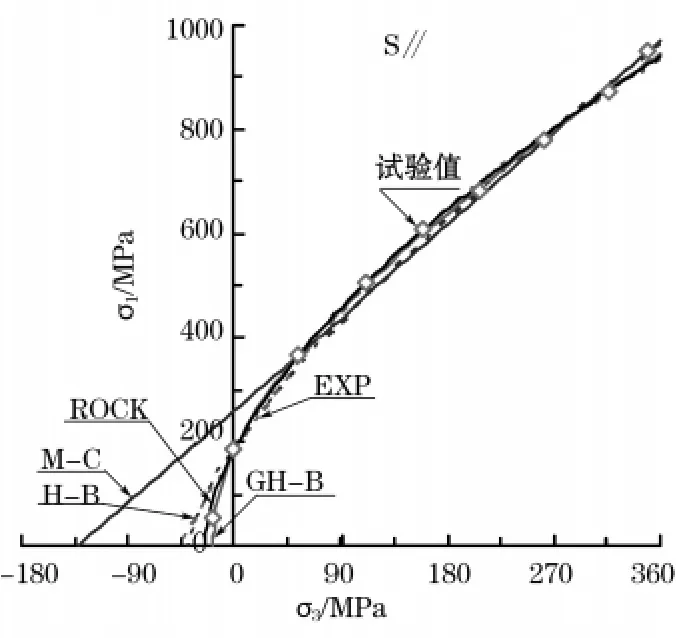
图4 砂岩平行层理的强度准则拟合曲线
3.4 Mesaverde砂岩
EXP准则对Mesaverde砂岩垂直层理和平行层里的试验数据拟合时,预测的单轴抗压强度分别是150.6MPa和174.6MPa,比试验值82.0MPa和99.0MPa分别偏高83.7%和76.4%;预测的单轴抗拉强度分别为28.66MPa和18.47MPa,是试验值10.01MPa和13.55MPa的近3倍,这显然是不合理的。
基于SS⊥和SS∥的试验数据,直接设定EXP准则单轴抗压强度的预测值为试验值,对其分别又进行一次拟合,拟合结果见表6和表7中*EXP所示。此时,EXP准则的平均拟合偏差稍有增加,其预测的单轴抗拉强度分别为12.68,18.47MPa,虽比试验值偏高,但相对于另外4种强度准则更接近真实值。
如图5,设定SS⊥的单轴抗压强度为试验值后,*EXP的拟合曲线在拉应力区域更接近抗拉强度的试验值数据点,但又明显偏离围压为30MPa附近的试验值点,SS∥的EXP和*EXP拟合曲线图与此相似,不再给出。试验过程中对SS⊥和SS∥加载的围压分别高达300MPa和400MPa,分别是单轴抗压强度试验值的近3.6倍和4倍,可能由于端部摩擦或其他原因,使得文献[10]中围压为30 MPa附近的试验值与真实情况不相符。尤明庆[1-2]也指出,指数强度准则可以凸显异常数据点。另外4种强度准则的拟合结果及相关参数值见表6和表7,其具体的拟合曲线图不再给出。
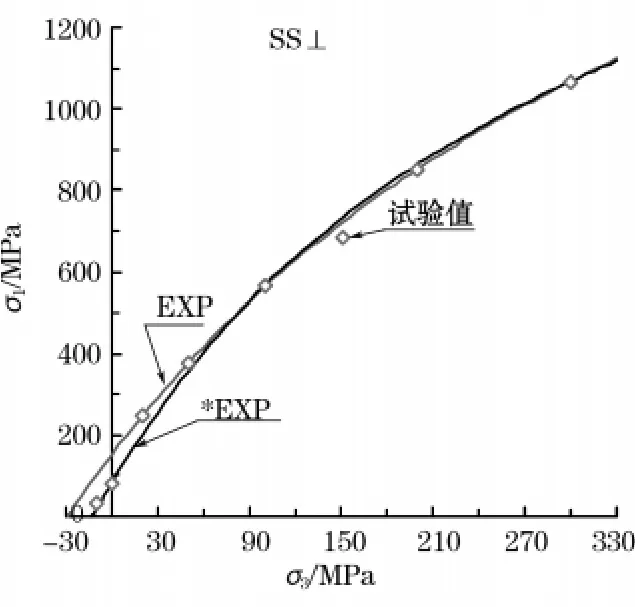
图5 Mesaverde砂岩垂直层理的EXP和*EXP拟合曲线
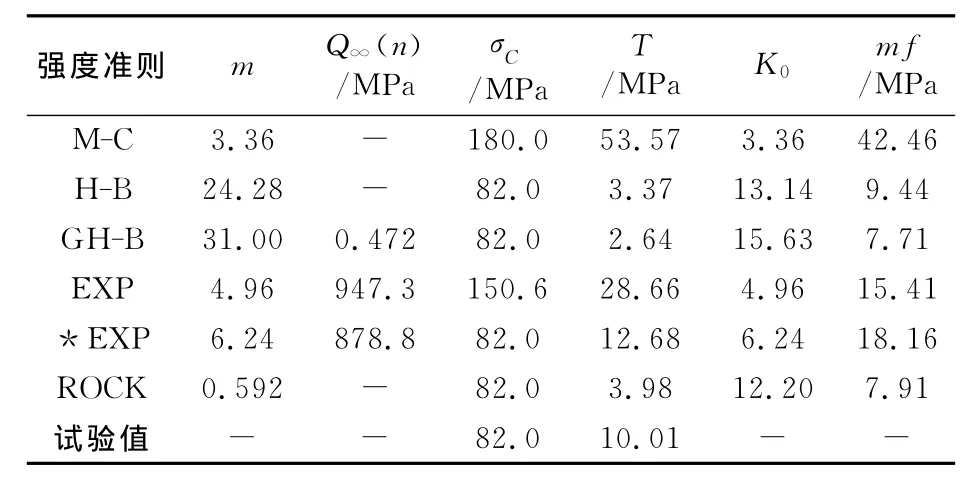
表6 Mesaverde砂岩垂直层理的拟合结果
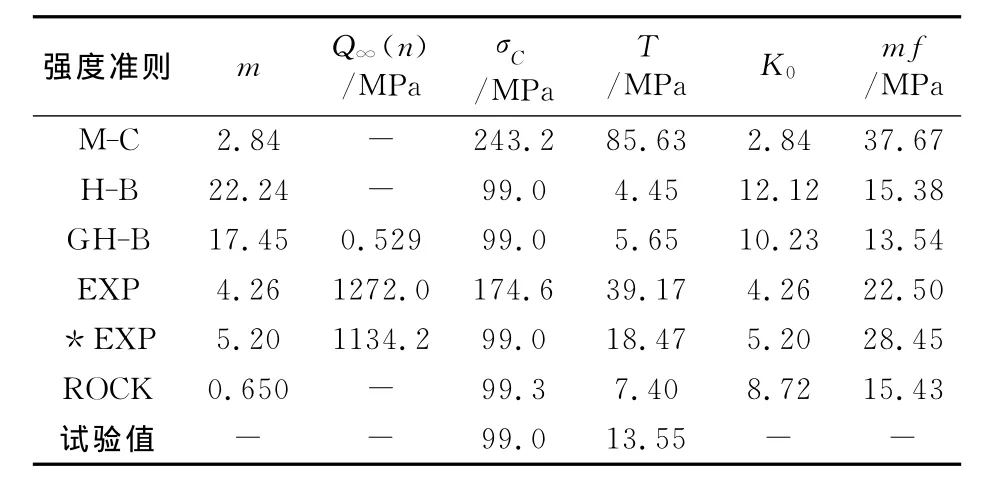
表7 Mesaverde砂岩平行层理的拟合结果
H-B准则、GH-B准则和ROCK准则对SS⊥和SS∥单轴抗压强度的预测值与试验值基本一致,但其对单轴抗拉强度的预测值仅是试验值的近一半甚至更低。GH-B准则的平均拟合偏差mf相对较小。
4 讨 论
直线型的M-C准则虽具有明确的物理背景,但不能预测岩石的单轴抗压强度;H-B准则对单轴抗压强度的预测略有偏差;而含有3个参数的强度准则都能预测单轴抗压强度值。
图7给出6种岩石的抗拉强度的综合偏差β和综合拟合偏差γ:
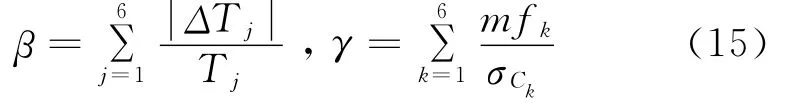
指数强度准则对SS⊥和SS∥试验数据的拟合结果选取*EXP。
由图6可以看出,直线型的M-C准则对抗拉强度的预测以及拟合偏差都最大。ROCK准则对抗拉强度的预测值与试验值最接近,其次是GH-B准则。EXP准则对抗拉强度的预测不如含2个参数的H-B准则,这是由于其拟合曲线在拉应力区近乎直线。GH-B准则的平均拟合误差mf最低,ROCK准则的与其相近,但略偏高。SS⊥和SS∥在围压为30MPa左右的试验数据可能与真实情况有差异,使得EXP准则的拟合偏差明显偏高。
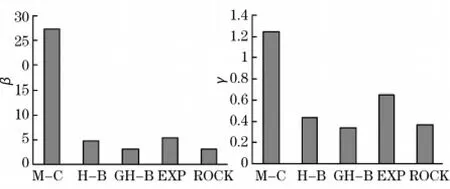
图6 5种强度准则的综合比较
抗拉强度远小于抗压强度,不会对强度准则的拟合结果产生明显影响。而将抗拉强度看作是强度准则拟合曲线的一个定点,如文献[5]中强制拟合曲线通过点(-T,3T),可能降低强度准则预测抗压强度的准确性和可行性。总的来说,用一个强度准则描述所有岩石的强度特性是很难的,甚至是不可能的。
5 结 论
(1)含有3个参数的GH-B准则、EXP准则和ROCK准则预测的单轴抗压强度与试验值基本一致;ROCK准则预测的抗拉强度与试验值较接近;GH-B准则具有较小的拟合偏差。
(2)抗拉强度对强度准则的拟合结果没有明显影响。
[1]尤明庆.岩石强度准则的数学形式和参数确定的研究[J].岩石力学与工程学报,2010,29(11):2172-2183.
[2]You M.Comparison of the accuracy of some conventional triaxial strength criteria for intact rock[J].International Journal of Rock Mechanics and Mining Science,2011,48(5):852-863.
[3]石祥超,孟英峰,李 皋.几种岩石强度准则的对比分析[J].岩土力学,2011,32(1):209-216.
[4]GHAZVINIAN A H,FATHI A,MORADIAN Z A.Failure behavior of marlstone under triaxial compression[J].International Journal of Rock Mechanics and Mining Science,2008,45(5):807-814.
[5]CARTER B J,DUNCAN S E J,LAJTAI E Z.Fitting strength criteria to intact rock[J].Geotechnical and Geological Engineering.1991,9(1):73-81.
[6]中华人民共和国水利部.水利水电工程岩石试验规程[M].北京:水利水电出版社,2001.
[7]HOEK E,BROWN E T.Empirical strength criterion for rock masses[J].ASCE Journal of Geotechnical Engineering Division,1980,106(GT9):1013-1035.
[8]HOEK E,CARRANZA TORRES C,CORKUM B.Hoek-Brown failure criterion-2002edition[C]∥Proceedings of NARMS-TAC 2002,Mining Innovation and Technology,Toronto:University of Toronto,2002:267-273.
[9]You M.True triaxial strength criteria for rock[J].International Journal of Rock Mechanics and Mining Science,2009,46(1):115-127.
[10]LIN W.Mechanical properties of mesaverde sandstone and shale at high pressures[R].Lawrence Livermore National Laboratory,1983.
[11]尤明庆,陈向雷,苏承东.干燥及饱水岩石圆盘和圆环的巴西劈裂强度[J].岩石力学与工程学报,2011,30(3):464-472.
国家自然科学基金资助项目(10572047).
2012-01-28)
付义胜(1984-),男,河南商城人,硕士研究生,从事岩石力学方面的研究工作,Email:fuyisheng1984@163.com。
