MATLAB在机械优化设计中的应用

曾怀灵，贺建国

（长沙矿山研究院有限责任公司， 湖南长沙 410012）

MATLAB在机械优化设计中的应用

曾怀灵，贺建国

（长沙矿山研究院有限责任公司， 湖南长沙 410012）

介绍了MATLAB优化工具箱中各种优化模型及其在机械优化设计中的应用，并给出了优化实例和结果。采用MATLAB优化工具箱来求解机械优化设计中的问题，不仅提高了设计效率，而且编程简单、结果可靠。

机械优化设计；MATLAB；优化模型；夹具设计

机械产品的设计，一般需要经过调查分析、方案拟定、技术设计、零件工作图绘制等环节［1］。传统的设计方法基本上是采取人工试凑和定性分析比较等粗略方法。而机械优化设计是以数学规划为理论基础，以计算机为工具，寻求最佳机械设计方案的现代设计方法，取代了传统的可行性设计［2］。目前，优化设计已有很多成熟的优化方法，都有各自的特点和适用范围。在MATLAB优化工具箱中就有很多实用的优化函数，利用这些优化函数去解决机械优化设计中的问题不仅方便实用，而且编程简单易懂。

1 MATLAB在机械优化设计中的应用

MATLAB（Matrix Laboratory）是由美国Mathworks公司开发的集数值计算功能、符号运算功能和图形处理功能于一身的超级科学计算语言。MATLAB有多个工具箱，其中优化工具箱（Optimization Toolbox）可以为线性、非线性最小化、非线性最小二乘、二次规划、方程求解、多目标优化等问题提供可靠的求解方法。

1.1 线性规划及其应用

线性规划在机械设计中应用非常少，主要是因其要求目标函数、约束条件都是线性的，而机械设计问题一般都是非线性的。目前，线性规划在一维下料问题中应用比较多，如文献［3］～［5］。求解线性规划问题常用的方法有单纯形法、大M法等。在MATLAB中由linprog函数来求解线性规划问题。线性规划模型如下：

式中，f、b、beq、lb、ub、x为向量，A、Aeq为矩阵。

linprog函数调用格式为：

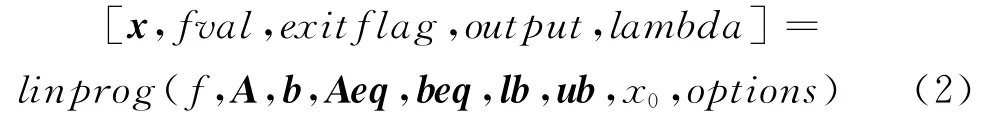
其中，x为线性规划的最优解；

fval为目标函数在最优解处的函数值（可省略）；

exitflag为迭代终止条件（可省略），为正数时，表示目标函数收敛于解x处；为负数时，表示目标函数不收敛；为零，则表示已经达到函数评价或迭代的最大次数；

output为优化详细信息输出（可省略）；

lambda为求得最优解的拉格朗日乘子（可省略），反应了各个约束条件在求解最优值的有效性；

f为目标函数；

x0为迭代初值（可省略）；

options设置优化项目参数（可省略）。

1.2 二次规划及其应用

通常把约束条件全为线性的而目标函数是二次函数的最优化问题称为二次规划［6］。二次规划在机械设计中的应用比较少，在文献［7］～［8］中利用二次规划法求解接触、有限元问题。在MATLAB中求解二次规划问题可用quadprog函数。二次规划模型如下：

式中，H为对称矩阵，其余参数意义同式（1）。

quadprog函数调用格式为：

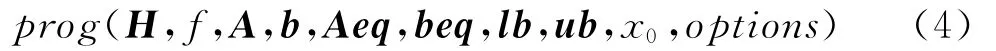
其中参数意义同式（2）。

1.3 无约束优化及应用

无约束优化有很多种算法，如最速下降法、Newton法、拟Newton法、共轭梯度法、信赖域法等。其中，拟Newton法利用了Newton法的二次收敛性使得可靠性更高，同时这种算法收敛速度也很快，所以在目前应用得相当广泛。而拟Newton法中应用比较多的主要有BFGS算法和DFP变尺度法。在MATLAB优化工具箱中求解无约束优化问题采用fminbnd函数、fminunc函数和fminsearch函数，其中默认的算法就是BFGS算法。fminunc函数和fminbnd函数要求目标函数必须连续，而函数fminsearch常用来处理不连续的函数。fminbnd函数可以求解区间［x1，x2］内单变量非线性函数的最小值。

无约束优化模型如下：

minf（x）

fminbnd函数调用格式为：

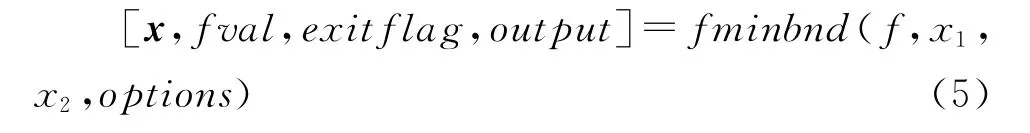
其中，x1、x2为求解区间上下界，其余参数意义同式（2）。

fminunc函数调用格式为：

其中，grad为目标函数在最优解处的梯度值，hessian为目标函数在最优解处的hessian矩阵值，其余参数意义同式（2）。

fminsearch函数调用格式为：

其中参数意义同式（2）。

1.4 有约束优化及应用

在机械优化设计中大多数问题是有约束优化问题。为了保证设计的机械零件安全可靠，设计时必须确定相应的设计准则，而这些设计准则就成了目标函数的约束条件［9］。这些设计准则包括强度准则、刚度准则、寿命准则、振动稳定性准则和可靠性准则，大多数是非线性的。对于非线性约束优化问题有很多解法，早期都是通过构造惩罚函数将有约束优化转换为无约束优化问题求解，而现在已经被更为有效的基于K－T方程解的方法所取代。在MATLAB优化工具箱中采用序列二次规划法（SQP）求解约束优化问题，采用的函数为fmincon函数。

有约束优化模型如下：

式中，C（x）、Ceq（x）分别为非线性函数，其余参数意义同式（1）。

fmincon函数的调用格式为：

其中，nonlcon为非线性约束条件包括C（x）和Ceq（x），其余参数意义同式（6）。

1.5 多目标优化及应用

对于大量的工程设计方案要评价其优劣，往往需要同时考虑多个目标。如在机械加工中，往往要求机械加工成本最低、生产率最高和刀具寿命最长。显然，这样的问题就属于多目标优化问题。多目标优化问题的求解方法很多，其中一种常用的方法就是将多目标优化问题重新构造一个函数，即评价函数，从而将多目标优化问题转化为求评价函数的单目标优化问题。这类方法主要有：主要目标法、线性加权和法、理想点法和极大极小法等。另一种是将多目标优化问题转化为一系列单目标优化问题来求解，这一类主要有分层序列法。在MATLAB中常用fminimax函数求解最大最小化问题，用fgoalattain函数求解多目标达到问题。

最大最小化问题模型如下：

式中，参数意义同式（8）。

fminimax函数的调用格式为：

其中，maxfval为在最优解处目标函数中最大目标函数的函数值，其余参数意义同式（9）。

多目标达到问题模型如下：

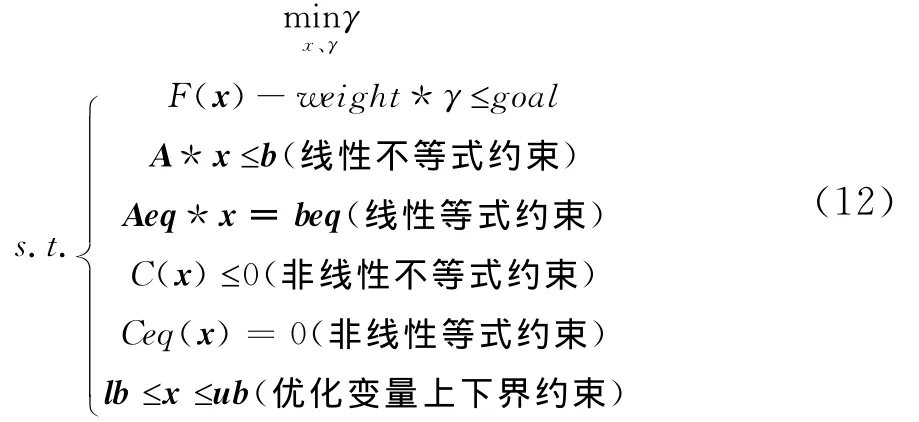
式中，goal变量为目标函数的目标值，weight变量为权重用于控制低于或超过fgoalattain函数指定目标的相对程度，其余参数意义同式（8）。

fgoalattain函数的调用格式为：

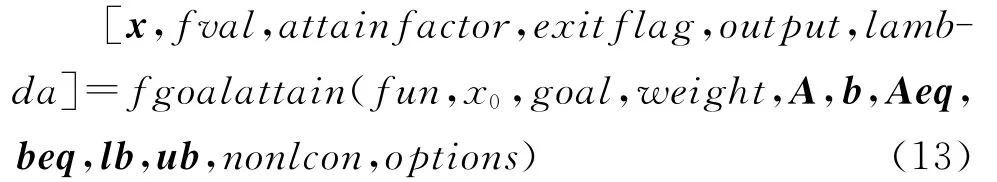
其中，attainfactor是目标达到情况，当attainfactor≥0时，目标达到值没有溢出；当attainfactor＜0时，目标达到值有溢出，其余参数意义同式（9）。

2 MATLAB优化工具箱应用实例

在矿用高强度圆环链材料力学性能的安标检验检测工作中，需要设计一对能承受350t（约3500 kN）拉力的实验夹具来连接拉力机和矿用高强度圆环链夹具。已知夹具的材料为45钢板材，屈服强度σs为355MPa，取安全系数s为1.2，要求设计的夹具质量最小（或体积最小）。根据设计要求，夹具上表面的尺寸及受力情况如图1所示。

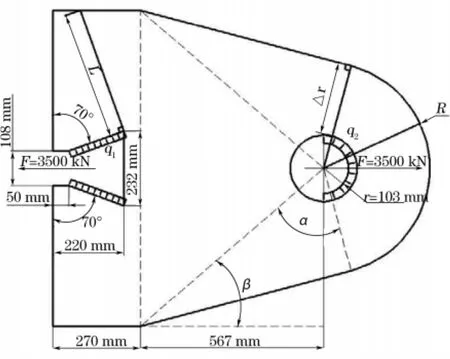
图1 夹具表面尺寸及受力示意

2.1 建立优化模型

通过分析，设夹具的设计变量为L、R（Δr＝R－r）以及板材的厚度h，设计目标为minV（L，R，h）：

根据设计准则得如下约束条件：

（1）对于V形槽面，夹具受力面在受力时不能被压溃：

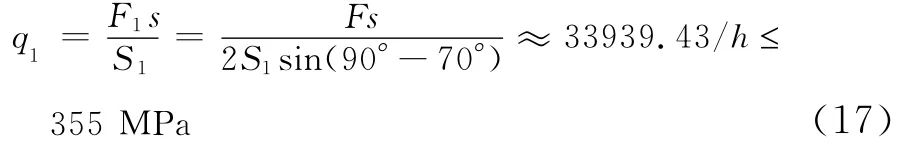
（2）对于圆孔面，夹具受力面在受力时不能被压溃：

（3）如图1所示，Δr处截面积最小，最易拉裂，为此需满足：

（4）由图1可知在V形槽面的L截面处存在最大弯曲应力，按照设计要求夹具计算弯曲应力应低于屈服强度（忽略应力集中影响）：

综合上述，约束条件化简后优化数学模型为：

2.2 MATLAB优化工具箱求解

（1）编写目标函数M文件myfun.m，其中L＝x（1），R＝x（3），h＝x（3）

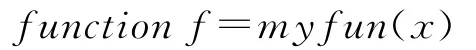
（2）编写约束函数M文件mycon.m

（3）编写运行程序M文件my.m

运行my.m文件，结果如下：

3 结 论

在机械设计中引入优化设计方法不仅能使设计的机械零件满足性能要求，还能使其在某些特定方面达到最优。利用MATLAB优化工具箱求解机械优化设计问题不仅避免了传统的设计方法中人工试凑、分析比较过程中的繁杂与重复，而且编程简单、结果可靠。在上述实例中，利用MATLAB软件中fmincon函数求解夹具设计问题，最终设计的夹具要比采用传统设计方法设计的质量轻、成本低，并且设计效率高。

［1］孙靖民.机械优化设计［M］.北京：机械工业出版社，2003.

［2］刘鹤松，姜 晶.基于MATLAB算法的机械优化设计［J］.煤矿机械，2004（11）：11－12.

［3］唐 健，刘 浩.从线性规划谈一维下料［J］.南京工程学院学报（自然科学版），2005，3（3）：1－5.

［4］王连杰.基于线性规划的一维优化下料系统研究与开发［D］.大连：大连理工大学，2003.

［5］张春玲，崔耀东.一维优化下料问题［J］.桂林工学院学报，2004，24（1）：103－106.

［6］曹卫华，郭 正.最优化方法及MATLAB的实现［M］.北京：化学工业出版社，2005.

［7］黄敬贤，张 杰.解弹性接触问题的二次规划法［J］.机械设计，1988（1）：1－6.

［8］孙惠学.二次规划法求解轴对称组合模具接触强度［J］.太原重型机械学院学报，1993，14（1）：79－84.

［9］濮良贵，纪名刚.机械设计［M］.北京：高等教育出版社，2001.

2012－02－24）

曾怀灵（1987－），男，湖南永州人，硕士研究生，主要从事机电液方向的研究与设计工作。