基于定权的多因子线性拟合方法研究
2012-11-16花向红尹志永
赵 言,花向红,尹志永
(1.武汉大学 测绘学院,湖北 武汉430079;2.天津测绘院,天津300381;3.武汉大学 灾害监测与防治研究中心,湖北 武汉430079)
基于定权的多因子线性拟合方法研究
赵 言1,2,花向红1,3,尹志永2
(1.武汉大学 测绘学院,湖北 武汉430079;2.天津测绘院,天津300381;3.武汉大学 灾害监测与防治研究中心,湖北 武汉430079)
通过综合曲线拟合与多因子线性拟合的特点,提出基于定权的多因子线性拟合方法用于多因子变形监测数据处理,实现基于定权的多因子线性拟合模型的建模过程,并与多元线性回归结果进行比对,同时对沉降变形监测的沉降量进行预测分析,验证模型的可行性和实用性。
定权;多因子;线性拟合;变形监测;变形预报
随着现代测量数据处理技术的不断发展进步,适用于多因子变形监测数据处理的方法逐渐增多,如多元线性回归、逐步回归、GM(1,n)等模型。这些多因子数据处理方法各有其特点和适用性,多元线性回归是利用所有因子等权重建模,但实际情况则是各个因子对监测变化量的影响程度不同,等权重对待不合理。本文通过多因子变形监测数据处理中权重分配方法的研究,提出基于定权的多因子线性拟合法,即通过单个因子变量建立监测值的曲线拟合模型,利用拟合值与实际监测值之间的差,确定每一个因子对监测变化量的影响程度。根据每个因子对监测变化量的影响程度和曲线拟合模型拟合值进行多因子线性拟合,利用后验差方法检验基于定权的多因子线性拟合模型的精度,并将基于定权的多因子线性拟合模型引入变形监测中处理多因子沉降监测数据,通过对某城市整体下沉监测数据的处理,并与常规多元线性回归结果进行比较分析,验证其可行性与实用性。
1 基于定权的多因子线性拟合模型
基于定权的多因子拟合模型由两部分组成,第一部分是利用每一个因子分别进行曲线拟合和确定每一个因子对监测变化量的影响程度;第二部分是利用第一部分求解得到的每个因子的拟合值和影响程度进行多因子线性拟合。
1.1 曲线拟合与确定因子的影响程度
在变形监测数据处理中,假设某地表沉降监测点变化量为y,y是随变量因子x1,x2,x3,…,xk变化而变化的函数,分别针对每一个变量因子xi利用曲线拟合法建立相应的yi函数。假设y=a0+a1x+a2x2+…+amxm,令

1.2 多因子线性拟合
根据式(2)求得的每个因子对应的拟合值和式(7)求得的每个因子的影响程度,对监测变化量进行多因子线性拟合,拟合值为^yi,如式(8)所示。
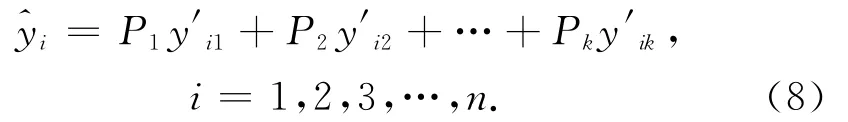
由式(8)计算得到的值即为基于定权的多因子线性拟合模型拟合值,根据建立的模型公式可以进行监测变化量的内插及预测。
在进行线性拟合过程中,如果某个因子或某些因子的权很小,以至于在拟合过程中可以忽略,那么可以考虑从拟合方程中删除该因子,此外,如果某个因子的变化趋势在过程中出现较多次突变,也可以考虑剔除该因子。在剔除时,把删除因子的权按照剩余因子的权重比值加到其他因子的权上,如第i0个因子权值太小,需要删除,Pi0的值分配如下:

根据式(9)求得的剩余各因子的权,那么删除变量因子后的模型拟合预测方程变为

由式(10)计算得到的值即为删除个别影响很小因子后的基于定权的多因子线性拟合值,可以根据该模型公式进行监测变化量的内插及预测。
2 基于定权的多因子线性拟合模型精度检验
对基于定权的多因子线性拟合模型精度(即模型拟合程度)评定的方法可以采用后验差方法进行检验,后验差检验是对残差分布的统计特性进行检验,它由后验差比值C和小误差概率P共同描述。
假 设 原 始 观 测 数 据 序 列 x(0)= {y(0)(1),y(0)(2),…,y(0)(n)},由基于定权的多因子线性拟合模型得x¯(0)={^y(0)(1),^y(0)(2),…,^y(0)(n)},计算残差
Δ(k)=y(0)(k)-^y(0)(k),k =1,2,3,…,n.
记原始数列x(0)及其残差数列Δ的方差分别为S21、S22,则

可得,后验差比值C=S2/S1,小误差概率P={|Δ(k)|<0.674 5 S1}。
表1列出了根据C、P取值的模型精度等级。模型精度等级判别式为
模型精度等级=max{P所在的级别,C所在的级别}。
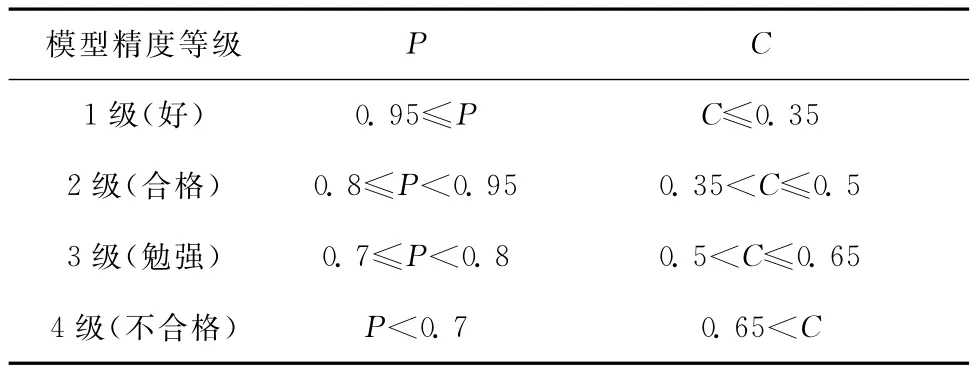
表1 模型精度等级
3 实例分析
3.1 基于定权的多因子线性拟合模型与多元线性回归模型精度比较
根据以上基于定权的多因子线性拟合模型建模原理,利用某城市41年的地表沉降数据和与之相关的3个因子(时间因子、地下水采用量与回灌累积差、降雨量与蒸发量累积差)的监测数据(见文献[2]),取其中连续的25期(见表2,(前20期用于建模,后5期用于模型预测效果评价))进行建模分析。从表2中可以看出,地表沉降累积量逐渐增大,时间因子、地下水采用量与回灌累积差也是不断增大的,而降雨量与蒸发量累积差在监测期间呈现升降变化,有时出现突变。因此,考虑连续性变化的要求,不选用第三个因子。对基于定权的多因子线性拟合模型经计算求得P1=0.498 9,P2=0.501 2,即线性拟合表达式可写为式(11)中,y′ik为单因子曲线拟合值,^yi为基于定权的多因子线性拟合模型拟合值。
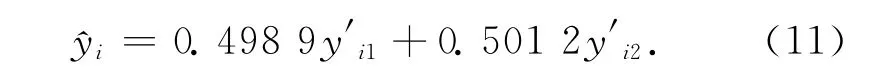
为比较逐步回归模型的拟合精度,同时对实验数据做多元线性回归建模分析,得到多元线性回归拟合模型方程
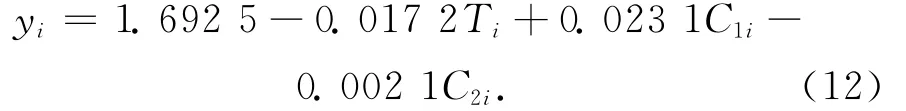
利用式(11)和式(12)建立的模型方程,对用于建模的前20期数据进行拟合,具体结果如表2所示。(T为观测时间,即时间因子,C1、C2分别对应其他2个变量因子(地下水采用量与回灌累积差和降雨量与蒸发量累积差),Δh为沉降监测值,Δh′为基于定权的多因子线性模型拟合值,Δh″为多元线性回归模型拟合值)
对以上建立的基于定权的多因子线性拟合模型和多元线性回归模型进行模型精度检验,验证其与实际监测值拟合程度的效果。根据后验差法[1]模型检验原理,分别计算S21、S′22和S″22。


表2 沉降监测值与2种拟合模型比较

根据后验差法模型精度等级表[1]可知,基于定权的多因子线性拟合模型C′<0.35且P′>0.95,即模型等级为1级(好);多元线性回归模型,C″<0.35且P″>0.95,即模型等级为1级(好)。结果表明,处理监测变化量和因子变化量都呈线性变化的数据时,基于定权的多因子线性拟合模型精度要比多元线性回归模型精度高或者二者精度相当。
因此,在处理呈线性连续变化的多因子监测数据时,除了选择多元线性回归外,可以考虑采用基于定权的多因子线性拟合模型。
从以上实验数据检验可以看出,基于定权的多因子线性拟合模型是在曲线拟合模型的基础上,分别就单一因子变量建立曲线拟合模型,然后再根据拟合模型差值求出各个因子对监测变化量的影响程度,进而确定各因子线性拟合方程的系数,实现对多因子监测数据的建模和拟合过程,在处理呈线性连续变化的多因子数据时表现出比多元线性回归模型更高的精度。基于定权的多因子线性拟合模型与多元线性回归模型拟合效果对比如图1所示。

图1 实际沉降监测值与基于定权的多因子线性拟合值及多元线性回归拟合值比较
从图1中可以看出,基于定权的多因子线性拟合模型拟合效果比多元线性回归的拟合效果好一些,且同实际沉降变化线的拟合程度很高。
3.2 基于定权的多因子线性拟合模型预测分析
根据建立的基于定权的多因子沉降监测线性拟合模型,对未来5期沉降量进行预测,如表3(T为观测周期,Δh为实际沉降监测值,Δh′为多基于定权的多因子线性拟合模型预测值)所示。
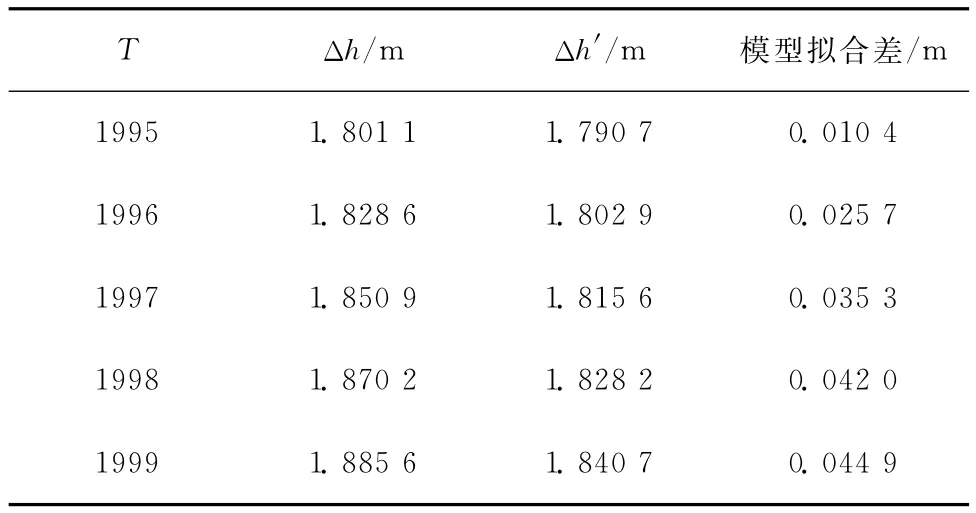
表3 基于定权的多因子线性拟合模型预测值
由表3可以看出,95年沉降预测值误差为0.010 4 m,96年沉降预测值误差为 0.025 7 m,97年沉降预测值误差为0.003 53 m,模型预测值与实际测量沉降值相差较小,误差率低,但是,随着预测期数的增加误差率逐渐增大,当误差率增大到一定值(一般为10%)则建立的拟合模型不再适用于预测。因此,在实际预测分析中要控制预测的周期数(一般控制在3期内),进行短周期预报分析。
4 结束语
通过对曲线拟合与多因子线性拟合模型的研究,提出基于定权的多因子线性拟合模型,给出模型的建模原理,用后验差方法检验其模型精度,并以分析处理沉降变形监测数据为例,利用沉降变化数据建立基于定权的多因子线性拟合模型,进行数据分析处理并与常规多元线性回归模型拟合值相比较。结果表明,基于定权的多因子线性拟合模型具有较好的预测分析效果,可用于处理变形监测中与多个因子相关且呈线性连续变化的测量数据。
[1]黄声享,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2010.
[2]陈正松.上海地区地面沉降的分析与预测[D].武汉:武汉大学,2008:30-31.
[3]陶本藻,蓝悦明.数字化曲线的最佳拟合[J].工程勘察,2004(3):46-47.
[4]葛朝霞,薛梅,宋颖玲.多因子逐步回归周期分析在中长期水文预报中的应用[J].河海大学学报:自然科学版,2009,37(3):255-257.
[5]杨敏,卢俊义.上海地区深基坑周围地面沉降特点及其预测[J].同济大学学报:自然科学版,2010,38(2):194-198.
[6]丁克良,欧吉坤,赵春梅.正交最小二乘曲线拟合法[J].测绘科学,2007,32(3):18-21.
Study on the multiple factors linear fitting methods based on weights-making
ZHAO Yan1,2,HUA Xiang-hong1,3,YIN Zhi-yong2
(1.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;2.Tianjin Institute of Surveying and Mapping,Tianjin 300381,China;3.Hazard Monitoring and Prevention Research Center,Wuhan University,Wuhan 430079,China)
By synthesizing the characteristics of curve fitting and multiple factors linear fitting,the multiple factors linear fitting model was presented to dispose the displacement monitoring data,realized the modeling process,and compared with the result of multivariate linear regression.Then by analysing the model of displacement monitoring data to verify the feasibility of the application of multiple factors linear fitting model to subsidence monitoring.
weights-making;multiple factors;linear fitting;deformation monitoring;deformation predicting
TU196
A
1006-7949(2012)04-0005-04
2011-07-09
国家自然科学基金资助项目(41074025)
赵 言(1988-),男,硕士研究生.
[责任编辑刘文霞]
