离散RCS的PWPF调制方式改进及混合控制逻辑设计
2012-11-16陆艳辉张曙光
陆艳辉, 张曙光
北京航空航天大学 交通科学与工程学院, 北京 100191
离散RCS的PWPF调制方式改进及混合控制逻辑设计
陆艳辉, 张曙光*
北京航空航天大学 交通科学与工程学院, 北京 100191
可重复使用飞行器(RLV)再入控制常涉及离散的反推力控制系统(RCS)和连续的气动舵面的混合控制,其中避免离散RCS出现极限环振荡和混合控制的逻辑是设计的关键问题。为此,对应用脉宽脉频(PWPF)调制的离散RCS进行极限环振荡行为的离散描述函数法预测,推导极限环出现条件,设计了一种前置非对称死区环节规避极限环而不损失性能,在此基础上提出便于工程应用的RCS与气动舵面混合控制逻辑。通过对典型飞行器的控制仿真验证表明,改进的离散RCS的PWPF调制方式及设计的混合控制逻辑能够获得良好的控制效果,满足控制要求。
再入; 反推力控制; 脉宽脉频调制; 极限环; 混合控制逻辑
可重复使用飞行器(Reusable Launch Vehicle,RLV)穿越大气层时,起初在高空气动舵面效率一般很低,通常采用反推力控制系统(Reaction Control System, RCS)提供操纵力矩。随着大气密度逐渐增加,气动舵面效率增强,逐渐过渡到应用气动舵面来节省RCS燃料,两者在一段时间内混合控制直到气动舵面提供足够的操纵力矩时,转至常规的气动舵面控制[1-2]。
RCS的基本工作机制是根据飞行操纵需求喷射高速气体产生操纵力矩,最基本的控制方式为邦-邦控制或者带死区的邦-邦控制,但是面临着消耗燃料较多等重要问题。为此,脉冲喷射控制更有优势。根据输出到RCS控制阀门的脉冲指令序列的调制方式,有脉冲宽度调制、脉冲频率调制和脉宽脉频调制等不同的方式[3-7],以满足连续的操纵力矩需求。Krovel提出了脉宽脉频(Pulse Width Pulse Frequency, PWPF)调制器参数选择原则和参数建议范围[3],McClelland将PWPF调制器与传统邦-邦控制器和时间最优邦-邦控制器进行了比较,显示PWPF调制器拥有较少的喷射次数、拟线性的使用特性以及较宽的设计空间等优点[6]。由于这些优点,PWPF调制器在工程中已得到较多的应用,如卫星、轨道机动飞行器等常采用PWPF调制技术进行姿态控制[5,7-8]。
但是,PWPF调制也有不利的问题。例如,非线性特性带来设计和分析困难,特别是可能因为附加的控制延迟产生极限环振荡等系统不稳定现象。除了设计和分析中的非线性问题,由于飞行控制广泛采用数字控制,Anthony和Wie分析了连续和离散PWPF调制存在的差异,并得出在一定情况下其影响不可忽视的结论[9]。当设计不慎,极限环振荡现象时有发生。另外,对于离散RCS的PWPF调制与连续舵面的混合控制问题,尽管已提出考虑约束的线性规划、链式控制分配、固定点搜索法、有效集理论和链式控制综合等算法[2,10-14],从实际应用的角度,也必须解决好相互激励、切换瞬态等问题。
本文从实际需求出发,针对提高离散PWPF调制器性能、避免极限环问题,研究设计改进方法,并应用于RLV再入时RCS与气动舵面的混合控制中,建立一种有效的混合逻辑。
1 PWPF调制器及其离散影响
连续PWPF调制器结构如图1(a)所示[3-6],根据操纵力矩需求指令r(t)(可设置前置增益进行调节)与RCS的工作状况y(t)(即正喷、反喷和不喷,可取值为1、-1、0)的差异e(t),驱动RCS喷射的改变,其中为了控制RCS喷射的频度、响应时机,设置一阶滤波器、施密特触发器(具有带滞环的继电器特性)。图中:km和τm分别为一阶滤波器的增益和时间常数;x(t)为输入给施密特触发器的一阶滤波信号;Uon和Uoff分别为施密特触发器的启动和关闭门限。
调制器对于阶跃输入响应如图1(b)所示,输出呈现出周期性的喷射(on)、不喷(off)特性,在一个周期内定义喷射时间Ton与喷射和不喷射Toff总时间之比为占空比[3-6]:
DC=Ton/(Ton+Toff)
(1)
随阶跃输入r幅值的改变,DC随之改变,当变化的线性度较好时,表明RCS的控制效果可用近似线性舵机等效。
实际使用时,常对输入进行标准化处理,将PWPF的输入转换为操纵力矩需求与提供最大输出力矩之比Mp的形式。当DC接近操纵力矩需求与输出力矩之比时,说明RCS具有良好的静态跟踪性能,进而可将其近似为增益为1的线性舵机,为设计提供便利。


图1 连续PWPF调制器Fig.1 Continuous PWPF modulator
具体设计中,PWPF参数的选择需要考虑实际约束,推力器喷射频率必须便于硬件实现且避开飞行器刚体的固有频率以免共振;滤波器时间常数的选取应保证推力器的延迟尽可能小,同时还要考虑燃料的损耗;滤波器增益的选取应使线性区域尽可能大,即减小死区和饱和区。较大的增益和较小的时间常数可以获得较高的调节精度,但是会增加发动机开关次数及燃料消耗;较大的施密特触发器迟滞h=Uon-Uoff会增加占空比非线性度和最小脉冲宽度,其中最小脉冲宽度为PWPF调制器最小工作时间,可推知为[3,5]
δmin=-τmln(1-h/km)≈hτm/km
(2)
Krovel[3]和Song等[5]经过分析后,提出了PWPF控制器参数建议范围,综合如表1所示。
表1PWPF调制器参数建议值[3,5]
Table1RecommendedparametervaluesforPWPFmodulator[3, 5]

kmτmUonh25⁃7501⁃0203⁃1002⁃08Uon
由于现代RLV飞行控制系统多为数字控制,直接基于离散描述的PWPF分析和设计,可以消除实现过程引入的附加误差。离散PWPF调制器结构如图2所示,相对于图1(a)的连续PWPF调制器,直接使用数字滤波器取代图1(a)的一阶(连续)滤波器。图中:m和n为数字滤波器的增益和时间延迟;反馈信号的引入有一拍的延迟,同时增置了增益k,便于更灵活的设计。
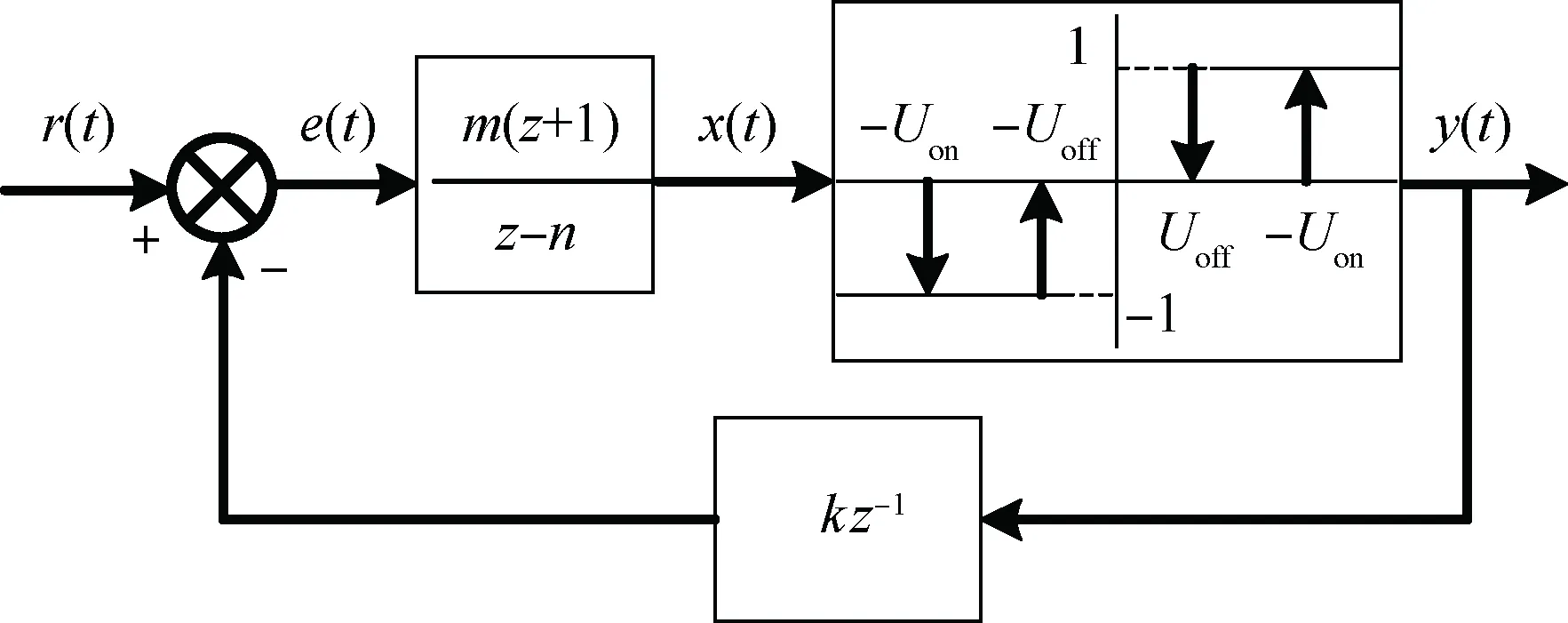
图2 离散PWPF调制器Fig.2 Discrete PWPF modulator
若计算周期为Ts,可得到离散和连续参数的关系:
{m=kmTs/(2τm+Ts)
n=(2τm-Ts)/(2τm+Ts)
(3)
本文从控制精度及燃料消耗角度进行权衡,选择Mp的死区为11%。调制器参数初步选择为
相应地,最小脉冲宽度:
δmin=10.3 ms
根据RCS硬件最小开关限制时间和飞行器结构频率,选择RCS指令计算周期:
Ts=60 ms
连续和离散PWPF的占空比如图3的实线和虚线所示。可以看出,相对于连续PWPF,离散调制器静态跟踪精度降低,而且当输入小于0.5时占空比线性度较差,主要原因在于计算周期Ts与δmin不协调所致。所以,需要进行参数调整。实际上计算周期已经实现了最小脉冲宽度,因此可取消滞环,取h=0,如图中点线,线性度得到改善。在此基础上调整反馈增益k,如图中带圈和三角符号的曲线,静态跟踪精度随之改变。综合考虑,调整后参数为
{h=0
k=0.8
进一步,考虑动态特性,离散PWPF跟踪幅值为50%的谐波操纵力矩输入响应特性如图4所示,为了便于对比,图中对输入指令和输出进行了积分(即对比冲量矩跟踪特性),其中谐波频率f=1,2,3 rad/s,可以看出,所选取的PWPF参数确保对于冲量矩指令具有良好的跟踪性能。

图3 PWPF占空比Fig.3 Duty cycle for PWPF modulator
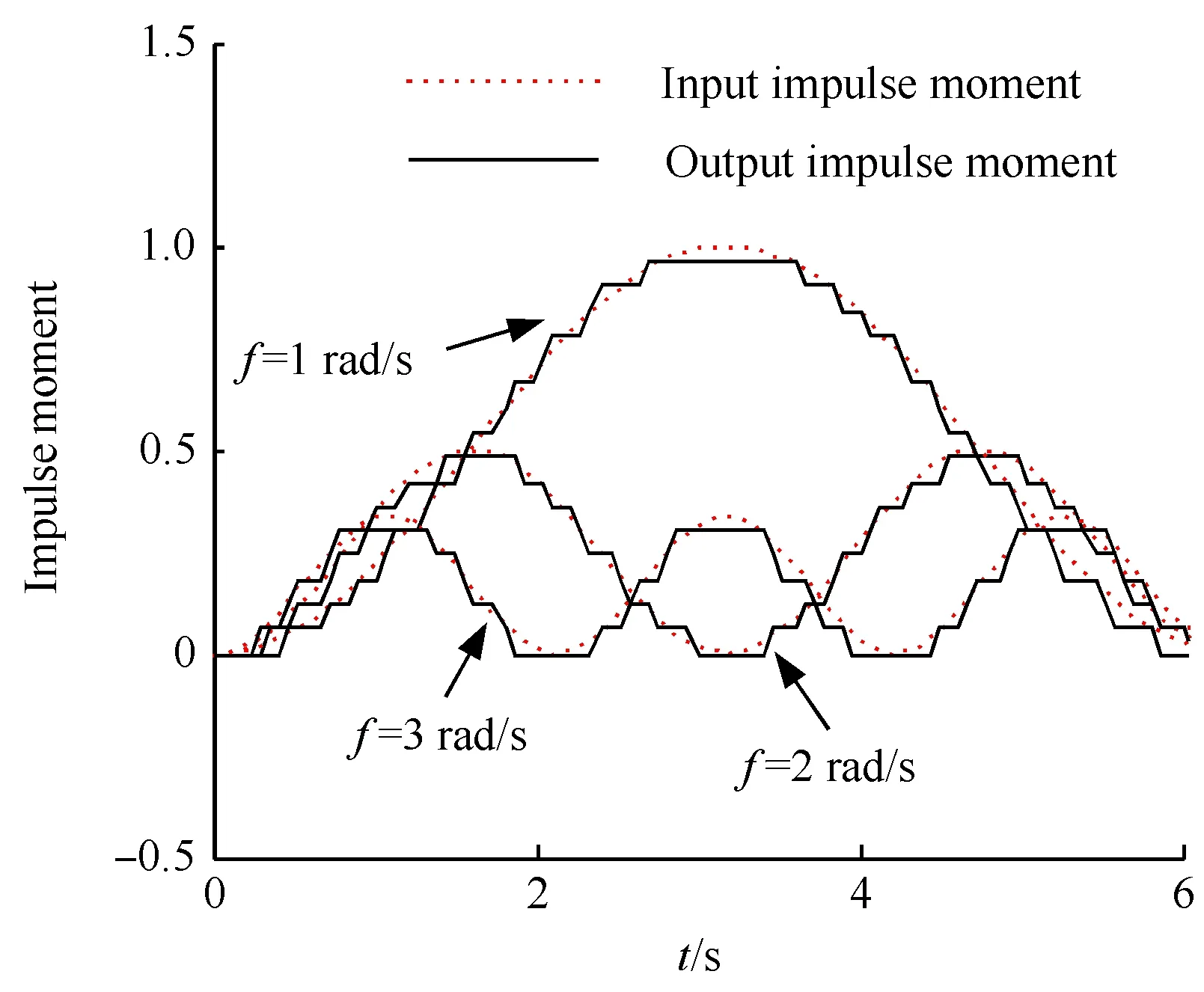
图4 离散PWPF动态跟踪性能Fig.4 Dynamic tracking performance for discrete PWPF
2 离散PWPF的极限环振荡和改进设计
2.1 极限环振荡
由于PWPF存在非线性环节,离散化后增加了系统延迟,从而增加了出现持续的自激振荡(极限环振荡)的可能性。基于第1节PWPF参数,当反馈增益k=1、Ts=60 ms时,输入幅值为1、频率为1 rad/s的离散正弦信号,5 s后撤掉指令将会激励图5(a)周期为4Ts极限环;输入离散正弦信号频率为0.5 rad/s、幅值为1, 5 s后撤掉指令将会激励图5(b) 周期为4Ts极限环。其中:图5(a)对应的极限环类型在一个振荡周期内正、负继电特性各持续1Ts,标记为Mc=1;图5(b)对应的极限环类型在一个振荡周期内正、负继电特性各持续2Ts,标记为Mc=2;类似,若一个振荡周期内正、负继电特性分别持续1Ts、2Ts或2Ts、1Ts,则极限环模式标识为Mc=1/2。


图5 离散PWPF的极限环振荡现象Fig.5 Limit cycle oscillation phenomena of discrete PWPF
更广泛地,对于PWPF非线性环节极限环周期为2Ts~5Ts的极限环模式如表2所示。

表2 可能的不同周期极限环模式Table 2 Limit cycle modes at different possible periods
对于这类带有非线性环节的离散系统,这里引入离散描述函数[15-16]方法分析极限环振荡存在范围。离散描述函数由Kuo[15]提出,假设非线性环节的输入为正弦调制脉冲序列,不同于连续描述函数只考虑输出基频部分,而是考虑真实输出,应用z-变换方法进行表达,分析非线性环节负倒离散描述函数的幅相特性,进而得到各个离散频率(采样周期的整数倍)极限环存在边界。
假设施密特触发器输入为正弦函数,即
(4)
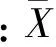
经过采样后得到正弦波调制的脉冲序列,其z-变换为

(5)
经过施密特触发器后,输出序列y(t)与谐波频率、幅值和相位等有关。根据可能的极限环振荡模式(见表2),对输出进行z-变换。以图5(a) 输出序列为例,则输出序列的拉普拉斯变换为

(6)
Y*(s)的z-变换形式为
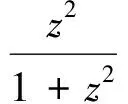
(7)
因此负倒离散描述函数为

(8)
式中:z=ejωcTs,对于图5(a)的输出序列,需要满足以下幅值和相位条件才能出现:
(9)
因此,

(10)
根据式(10)可在复平面内计算此型极限环振荡的范围,若线性环节相同频率(对于本例为Tc=4Ts,其中Tc为极限环周期)落在此型极限环边界内,则会出现相应类型的极限环振荡。
根据离散描述函数[15-16],死区环节的极限环区域在复平面内关于实轴对称。设极限环周期Tc=NcTs(Nc=2,3,…,∞)时,随Nc增加,极限环区域将趋近于负实轴;当Nc为大于2的偶数时,以Tc=4Ts极限环区域最大,当Nc为奇数时,Tc=3Ts极限环区域最大。根据此特点,计算周期为2Ts、3Ts和4Ts的边界,极限环分析结果如图6所示。其中,线性环节离散传递函数为

(11)


图6 离散PWPF的描述函数分析Fig.6 Describing function analysis for discrete PWPF
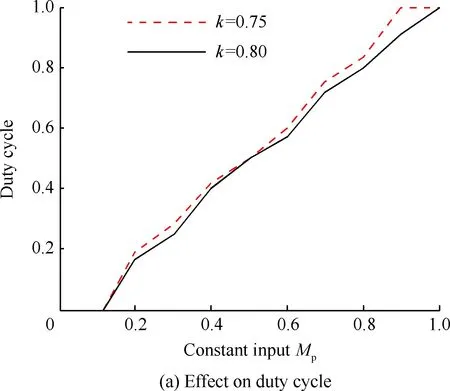
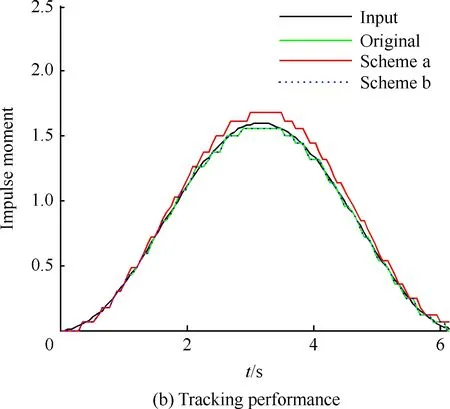
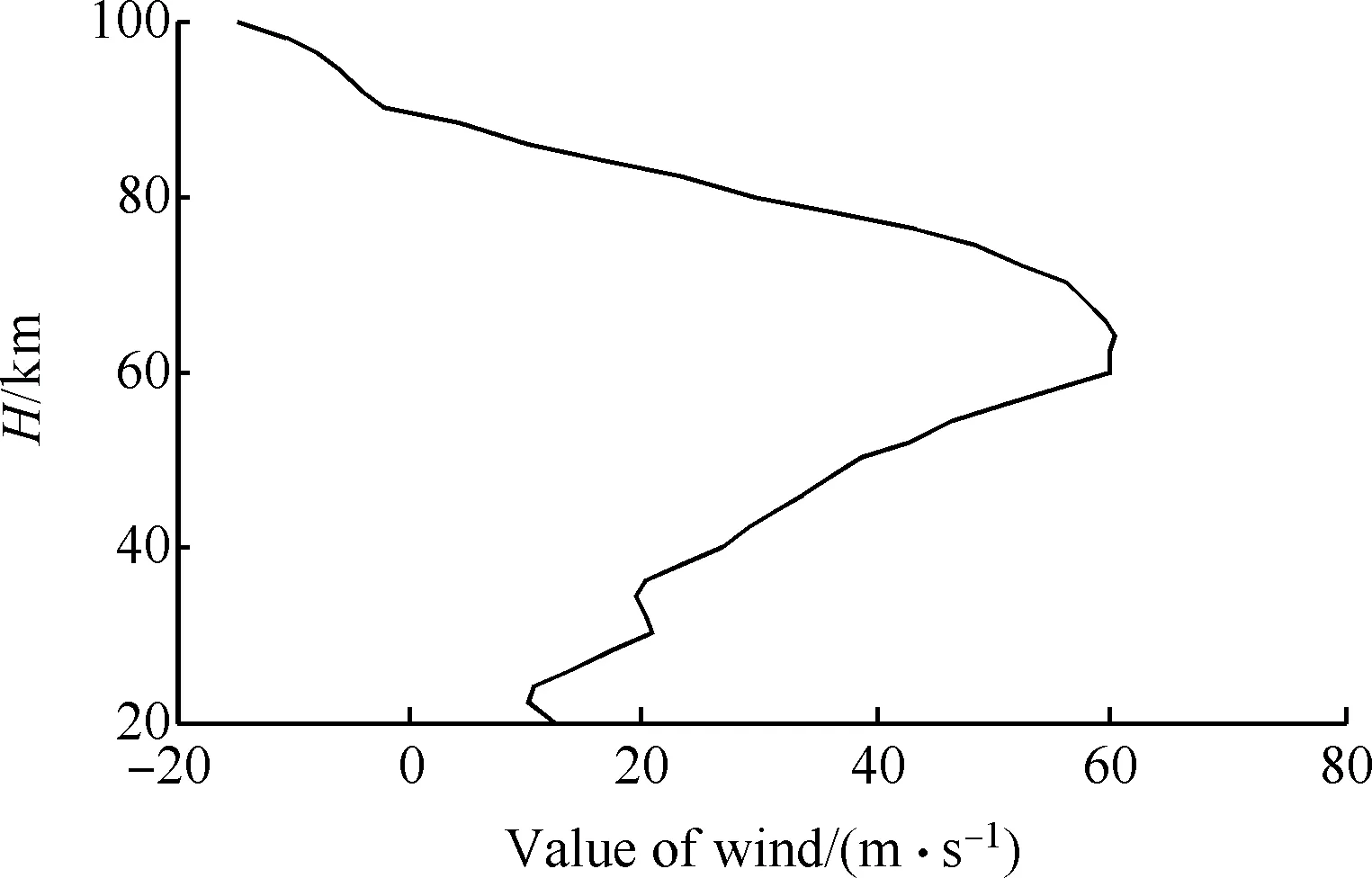
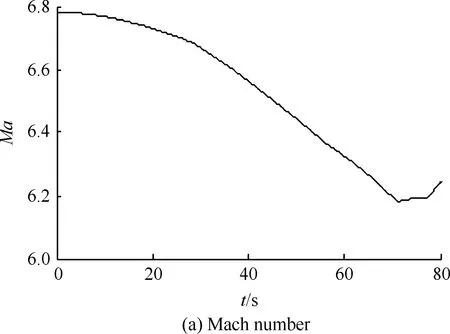
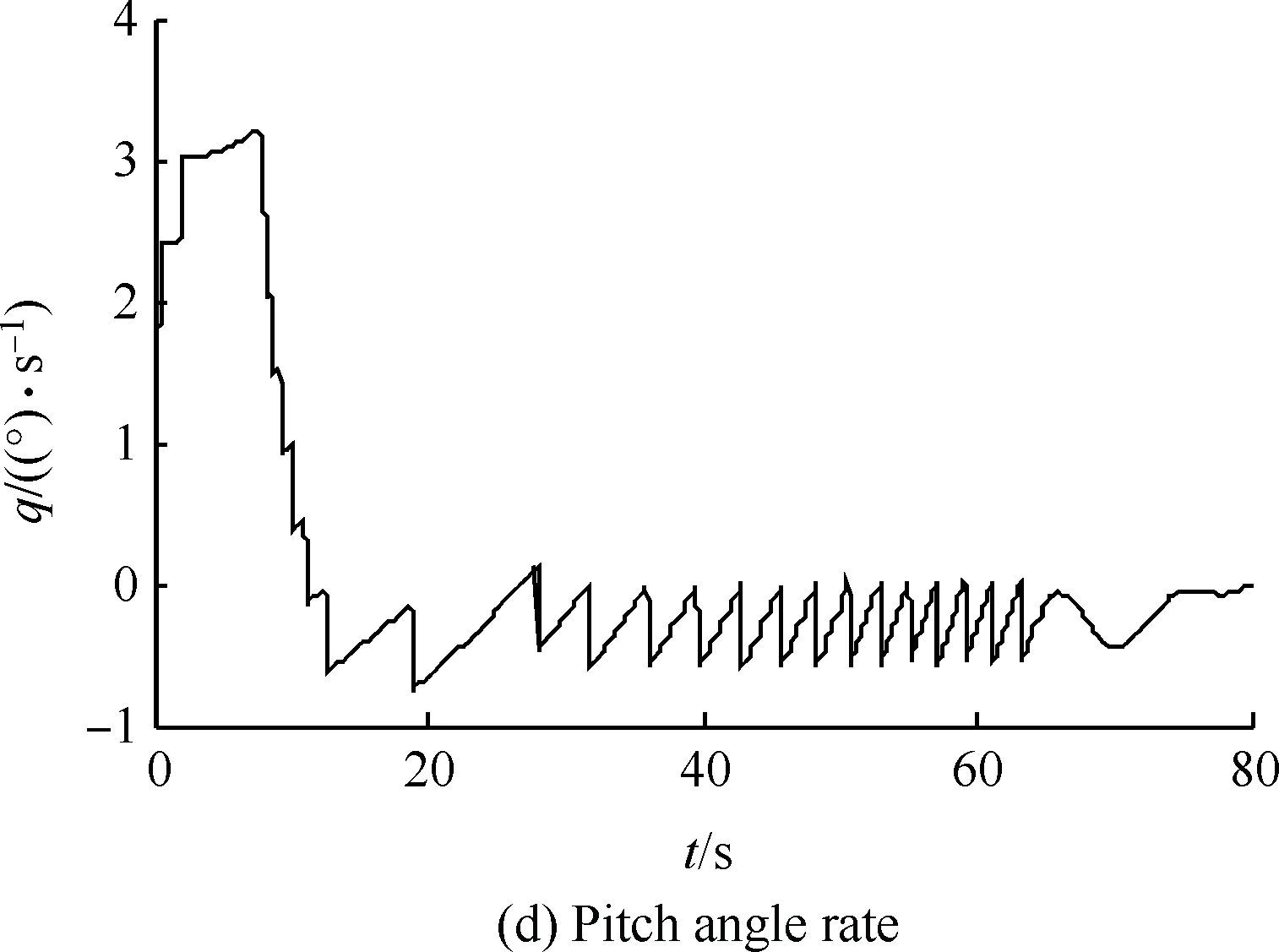
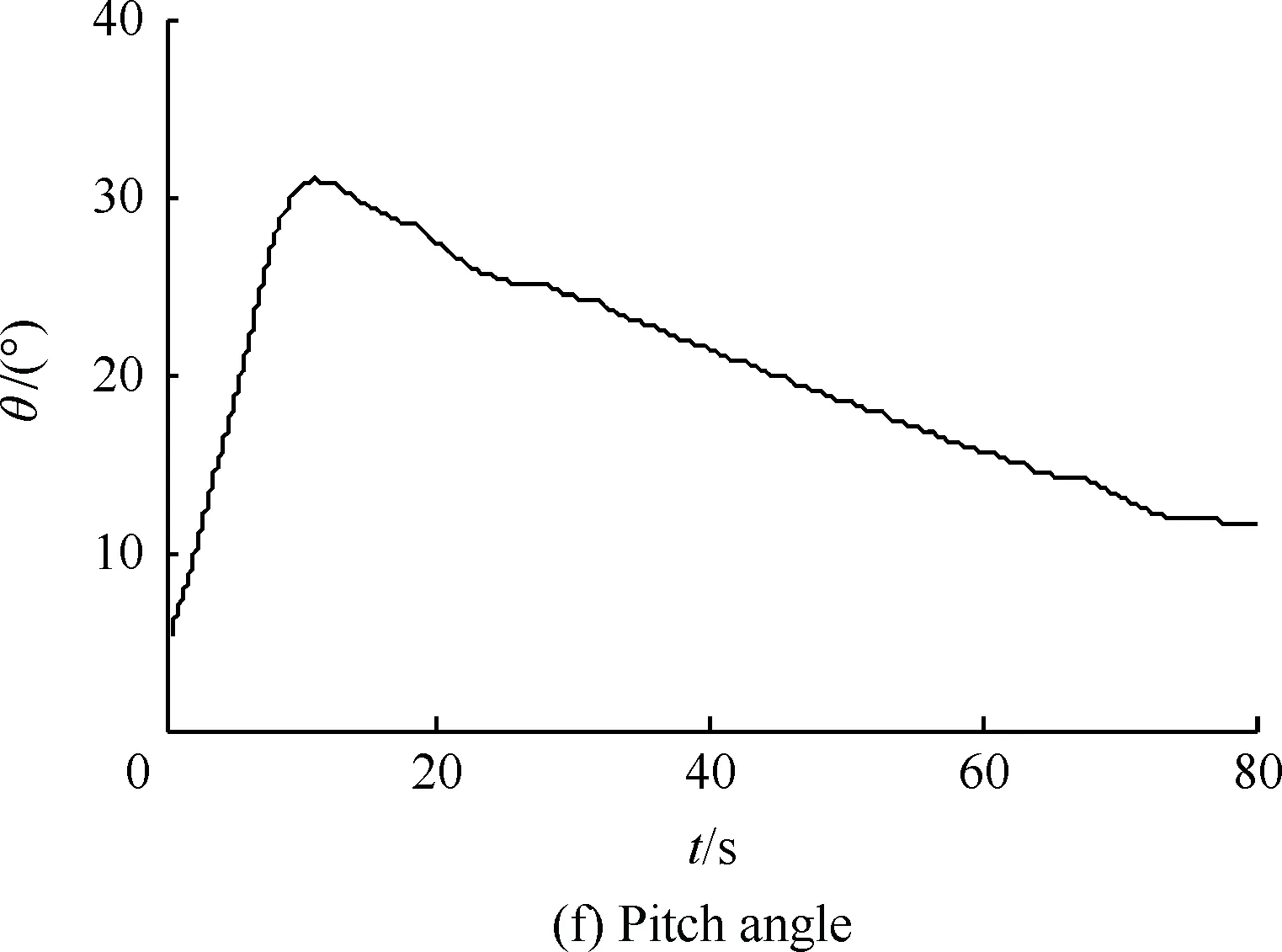
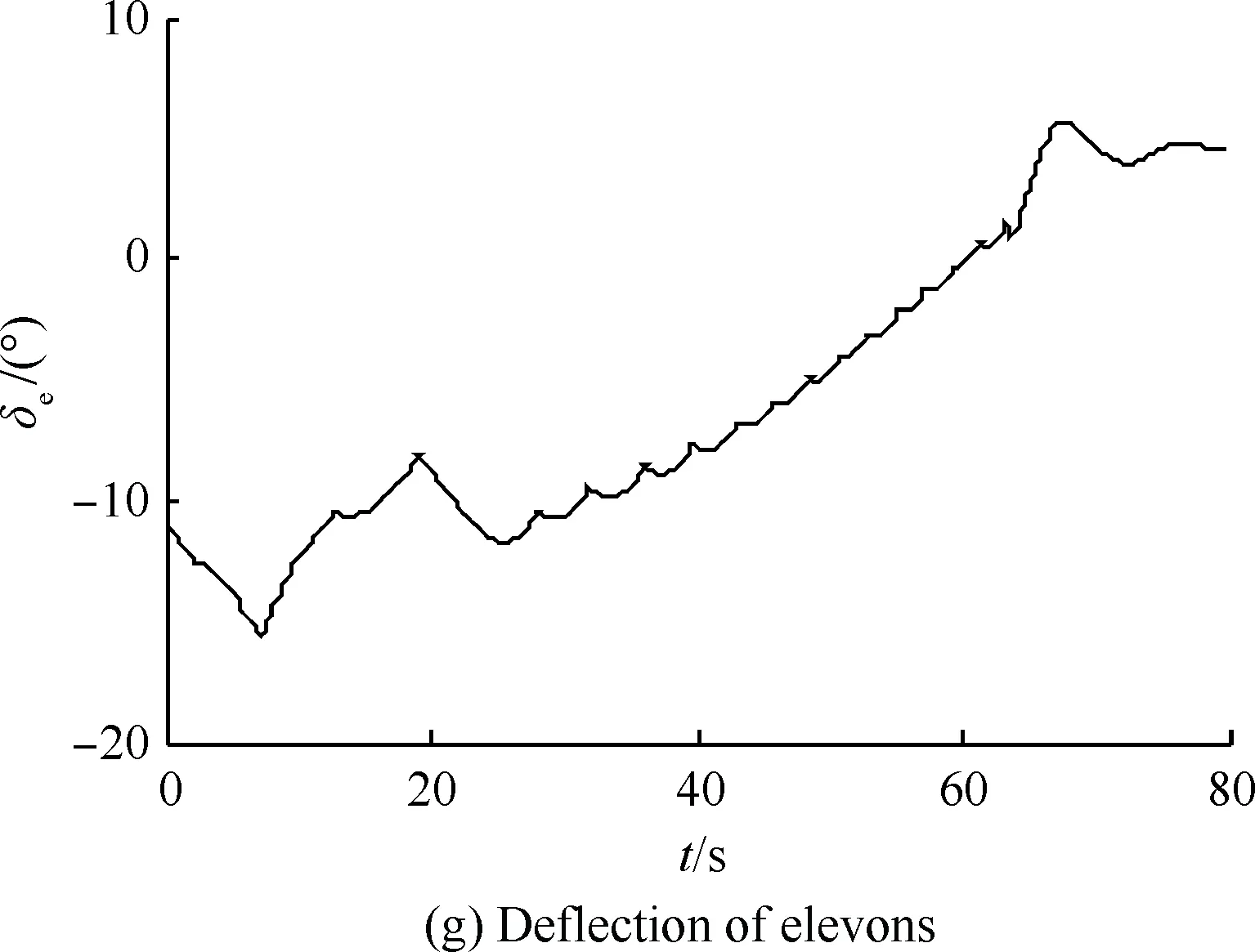
由图6可以看出,线性环节G(z)与非线性部分交叠区随着k增加而增加。Tc=4Ts的极限环区域最大(见图6(a)图),Tc=3Ts的极限环区域相对较小(见图6(b)图),Tc=2Ts的极限环区域缩为-Uon沿负实轴的射线(见图6(b)图);其他更大周期的极限环区域都明显小于3Ts和4Ts情况(分别对应奇数、偶数倍周期)。在0.5 2.2 离散PWPF极限环的改进设计 2.1节采用离散描述函数方法预测了极限环存在范围。如果降低增益k可回避极限环,但有时会损失性能。为此,本文设计前置非对称死区,使得在零输入r≡0时,前向出现非零值Δ(其中Δ≥0),改变环路的对称性,进而用于回避极限环振荡,如图7所示,其中Improved PWPF块指图2增加可调增益k的离散PWPF调制器。 图7 带非对称死区的离散PWPF调制器Fig.7 Discrete PWPF modulator with asymmetric dead zone 以图5(a)的极限环类型为例,采用递推方式,分析非对称死区回避极限环的有效性。 设a为施密特触发器节初始输入值,b为e(t)的初始值,离散PWPF输出序列为 y(t)=1,0,-1,0,1,0,-1,0,… 当时间序列N=0,1,2,3,…,递推规律如下: (12) (13) 由于|n|<1,数列收敛于 (14) (15) 若存在极限环,则要求 (16) 将式(3)代入式(16),得到 (17) 当Δ=0时,此类极限环存在条件: (18) 当k确定,则此类极限环存在条件: (19) 当选取第1节PWPF参数,且Δ=0时,形成此类极限环条件为0.766 9≤k≤5.112 5,与描述函数法分析接近(描述函数法假设了谐波输入,这里的递推是准确分析)。当k=1.0时, 与图5(a)仿真结果一致。 在特定k值下,可通过调整Δ回避极限环振荡。例如k=0.8时,当Uon/km>Δ>0.004 9时,不存在极限环振荡,上界Uon/km主要考虑实际力矩需求为零时,RCS不进行动作。 对于图5(b)类型极限环,推导方式类似。综上所述,调整前置死区可回避极限环。基于第1节PWPF基本参数,回避图5两种极限环的措施如表3所示。表4列出最终两组调制器参数方案。 表3 极限环回避方法Table 3 Methods to eliminate limit cycles 表4 PWPF调制器参数方案Table 4 Scheme for PWPF modulator parameters 两组参数方案的时域对比如图8所示,其中动态跟踪最大输入为80%的谐波力矩需求,其频率为1 rad/s。由图可以看出,使用降低k(方案a)回避极限环,将会降低跟踪性能;而使用加入非对称死区方式(方案b),则可在不损失跟踪性能的情况下,回避极限环。因此,可选择方案b为最终设计参数方案。 图8 两种回避极限环策略对比Fig.8 Comparison of two schemes to eliminate limit cycles PWPF调制器将离散RCS控制转化为近似连续控制面,为设计提供了便利,而再入过程还需考虑气动舵面与RCS混合控制。根据实际工程应用需求,混合控制主要考虑以下因素: 1) 节省RCS燃料,优先使用气动舵面。 2) 不同操纵面避免相互激励振荡。 3) 切换瞬态小。 4) 设计与评价简单,尽量借鉴已有经典控制评价体系。 5) 有较好的操纵品质。 根据以上要求,以纵向迎角控制为例,提出如图9的混合控制逻辑。RCS与气动舵面混合通过升降舵的操纵限幅及混合参数kblend实现,具体如下: (20) 图9 再入飞行迎角控制通道的混合逻辑Fig.9 Mix control logic of angle of attack command at re-entry flight 图9所示控制逻辑体现如下特点: 1) 根据动压调整升降舵操纵项的限幅值δe·ul和δe·ll,较小动压时,俯仰RCS用于操纵,升降舵只用于积分配平;升降舵操纵权限随动压增加逐渐放开,实现节省燃料及不同操纵面的光滑过渡。 2) 混合参数kblend使得在升降舵操纵不足时启用RCS,避免相互激励振荡。 3) 气动舵面和RCS分时工作,可分别设计后混合,设计简便。 4) PWPF调制器使得RCS控制近似为增益1,延迟为计算周期一半的线性连续舵机,设计较为方便。 图10 典型GRAM95风场剖面Fig.10 A typical wind profile from the GRAM95 model 仿真结果如图11所示,图中:Ma为马赫数;H为海拔高度;α和αcmd分别为迎角和迎角指令;q为俯仰角速度;θ为俯仰角;δe为升降舵偏度,RCScmd为俯仰RCS指令。 图11 再入飞行控制仿真结果Fig.11 Simulation for re-entry flight control 由图11可看出,迎角跟踪过渡态平顺,稳态误差小。返回初始,为了跟踪迎角指令,RCS使用较为频繁;当动压大于1 kN/m2后,升降舵逐渐介入控制,RCS使用减少。总体而言,RCS用量及喷射次数较少;且RCS开关时,升降舵抖动幅值和频率均较低,使得运动比较平顺。 与采用优化算法的混合控制策略相比,这里的混合分配逻辑比较简便、通用,算法收敛性及实时性均较优,工程应用性强。但由于混合逻辑相对简单,对于追求最优化的控制目标(如燃料最省)时,需要进一步考虑其他优化算法。 1) 为了消除离散PWPF调制器的极限环振荡,可以增加可调反馈增益并合理调节其值,但是需要与跟踪特性权衡考虑。本文基于离散描述函数方法有效预测了离散PWPF调制器的极限环参数范围,所设计的前置非对称死区与可调反馈增益结合使用,较好地兼顾了跟踪特性和极限环抑制需求。 2) 气动舵面和RCS分时工作,可分别设计后混合。本文设计的混合逻辑通过仿真验证表明能够充分满足设计需求。 [1] Doman D B, Gamble B J, Ngo A D. Quantized control allocation of reaction control jets and aerodynamic control surfaces. Journal of Guidance, Control, and Dynamics, 2009, 32(1): 13-24. [2] Ning G D.Reentry dynamics analysis, guidance and control for reusable launch vehicle. Beijing: Beihang University, 2007. (in Chinese) 宁国栋. 可重复使用航天器再入动力学特性分析及制导控制研究. 北京: 北京航空航天大学, 2007. [3] Krovel T D. Optimal tuning of PWPF modulator for attitude control. Trondheim, Norway: Norway University of Science and Technology, 2005. [4] Guo Q C. Research of constant thrust attitude control method. Harbin: Harbin Institute of Technology: 2006. (in Chinese) 郭清晨. 常值推力姿态控制方法研究. 哈尔滨:哈尔滨工业大学,2006. [5] Song G B, Nick V B, Agrawal B N. Spacecraft vibration reduction using pulse-width pulse-frequency modulated input shaper. Journal of Guidance, Control, and Dynamics, 1999, 22(3): 433-440. [6] McClelland R S. Spacecraft attitude control system performance using pulse-width pulse-frequency modulated thrusters. California: Naval Postgraduate School, 1994. [7] Wang Q, Yang B, Ma K M. PWPF optimizing design and its application research to terminal guidance of kenetic killing vehicle. Journal of Astronautics, 2005,26(5):576-580. (in Chinese) 王清, 杨宝, 马克茂. 一种优化 PWPF 调节器在动能拦截器末制导中的应用研究. 宇航学报, 2005,26(5):576-580. [8] Frost S A. A framework for optimal control allocation with structural load constraints. AIAA-2010-8112, 2010. [9] Anthony T C, Wie B. Pulse-modulated control synthesis for a flexible spacecraft. Journal of Guidance, Control and Dynamics, 1990, 13(2):1014-1021. [10] Bolender M A, Doman D B. Non-linear control allocation using piecewise linear functions:a linear programming approach. AFRL-VA-WP-TP-2004-303, 2004. [11] Servidia P A, Pea R S. Spacecraft thruster control allocation problems. IEEE Transactions on Automatic Control, 2005, 50(2): 245-249. [12] Durham W C. Constrained control allocation. Journal of Guidance, Control, and Dynamics, 1993, 16(4): 717-725. [13] Page A B, Steinberg M L. A closed-loop comparison of control allocation methods. AIAA-2000-4538, 2000. [14] Paradiso J A. Application of linear programming to coordinated management of jets and aerosurfaces for aerospace vehicle control. CSDL-R-2065, 1988. [15] Kuo B C. Analysis and synthesis of sampled-data control systems. Englewood Cliffs N.J.: Prentice-Hall, Inc, 1963: 471-493. [16] Gelb A, Vander Velde W E. Multiple-input describing functions and nonlinear system design. New York: McGraw-Hill Book, 1968: 476-492. [17] Rockwell International. Aerodynamic design data book. Volume 1 M orbiter vehicle STS-1. SD72-SH-0060-1M, 1980. [18] Justus C G, Jeffries W R III, Yung S P, et al. The NASA/MSFC global reference atmospheric model-1995 version (GRAM-95). NASA TM-4715, 1995. AnImprovementonPWPFModulationofDiscreteRCSandDesignoftheBlendedControlLogic LUYanhui,ZHANGShuguang* SchoolofTransportationScienceandEngineering,BeihangUniversity,Beijing100191,China There-entrycontrolofreusablelaunchvehicles(RLV)ofteninvolvesbothdiscretereactioncontrolsystem(RCS)andcontinuousaerodynamiccontrols,inwhichtheavoidanceoflimitcyclesandtheblendedcontrollogicarethekeyissuesofdesign.Inthispaperthelimitcycleoscillationbehaviorofthediscretepulse-widthandpulse-frequency(PWPF)modulationispredictedbyapplicationofthediscretedescribingfunctionanalysistechnique,theappearanceconditionsarethenderived,andanasymmetricdeadzoneisfurtherconstructedandusedintheforwardpathtoeliminatethelimitcycleoscillations,withoutperformanceloss.BasedontheimprovedPWPFmodulation,aRCSandaerodynamicsurfacesblendedcontrollogicisdesignedwithconcernonimplementation.SimulationsonthecontrolofatypicalRLVshowthattheimproveddiscretePWPFmodulationandtheblendedlogicworksatisfactorilytotherequirementsofcontrol. re-entry;reactioncontrolsystem;pulse-widthandpulse-frequencymodulation;limitcycle;blendedcontrollogic 2012-01-13;Revised2012-02-20;Accepted2012-03-04;Publishedonline2012-03-291140 URL:www.cnki.net/kcms/detail/11.1929.V.20120329.1140.008.html .Tel.:010-82315237E-mailgnahz@buaa.edu.cn 2012-01-13;退修日期2012-02-20;录用日期2012-03-04; < class="emphasis_bold">网络出版时间 时间:2012-03-291140 www.cnki.net/kcms/detail/11.1929.V.20120329.1140.008.html .Tel.:010-82315237E-mailgnahz@buaa.edu.cn LuYH,ZhangSG.AnimprovementonPWPFmodulationofdiscreteRCSanddesignoftheblendedcontrollogic.ActaAeronauticaetAstronauticaSinica,2012,33(9):1561-1570. 陆艳辉,张曙光.离散RCS的PWPF调制方式改进及混合控制逻辑设计.航空学报,2012,33(9):1561-1570. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 1000-6893(2012)09-1561-10 V412.4 A 陆艳辉男, 博士研究生。主要研究方向: 高超声速飞行动力学与控制。 Tel: 010-82317703 E-mail: luyanhuiboy@163.com 张曙光女, 博士, 教授, 博士生导师。主要研究方向: 飞行力学与飞行控制、 复杂系统安全性。 Tel: 010-82315237 E-mail: gnahz@buaa.edu.cn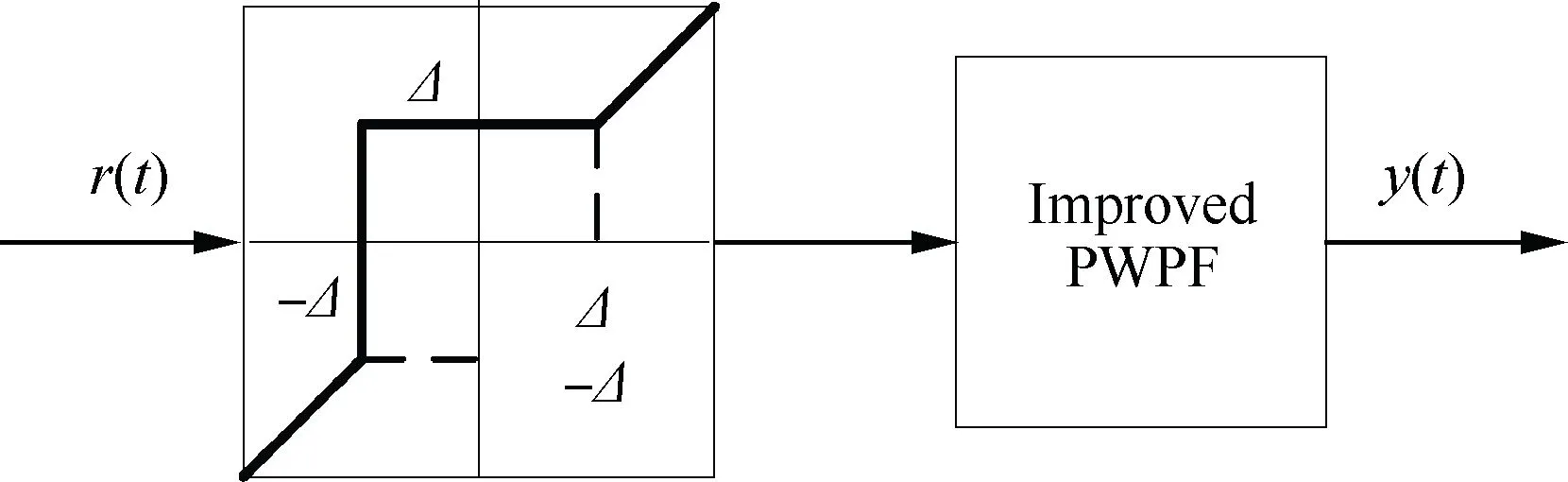
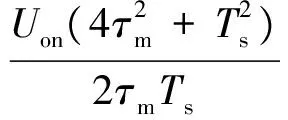


3 RCS与气动舵面混合控制逻辑
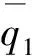

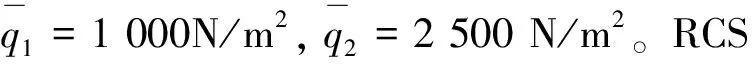




4 结 论
