MATLAB程序在对污染物主成分分析及预测中的应用

郑媛媛

（深圳市环境科学研究院，广东 深圳518006）

1 引言

在近几年中，城市进行了大量的旧房拆迁及扩建工程，使降尘量增大，可吸入颗粒物也不断逐步向上发展，造成了浓度的增加。所以，利用2001～2006年的主要污染物浓度和MATLAB技术来分析和预测大气环境主要污染物的变化趋势，基础数据见表1。

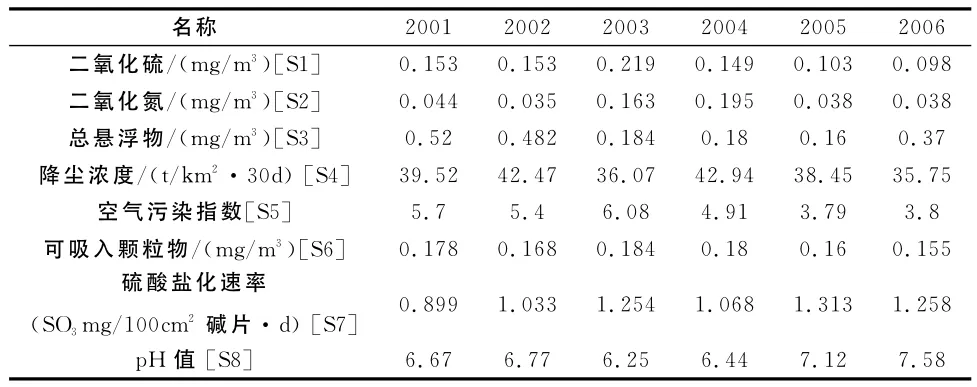
表1 2001～2006年空气主要污染物浓度

2 主成份分析的MATLAB的实现

2.1 使用协方差矩阵进行主成分分析

［PC，LATENT，EXPLAINED］＝pcacov（X）

式中，X为原始指标矩阵的协方关矩阵；PC为主成分（按列放置）；LATENT为协方差矩阵的特征值；EXPLAINED为每个主成分解释的方差量占总方差量的百分比。

2.2 直接利用原始为进行主成分分析

以下式中，X为原始数据矩阵（每一行代表一个样本，每一列代表一个指标）；返回SCORE为Z分数；返回TSQUARE为Hotelling的T2统计量；Z分数是通过将原始数据转换到主成分空间中得到的数据，LATENT向量的值为SCORE的列数据的方差；Hotelling的T2统计量为来自数据集合中心的每一个观测量的多变量距离的度量。

具体分析的编程如下：

%c9fun9＿1

clear all；clc

%将原始数据样本矩阵赋值给X；

covX＝cov（X）；%得到原始数据矩阵的协方差矩阵

［PC，LATENT，EXPLAINED］ ＝ pcacov（covX）；%主成分分析

disp（＇综合因子＇）；PC

disp（＇特征值＇）；LATENT

disp（＇某一综合因子解释方差占总方差的百分比%＇）；EXPLAINED

［n，m］＝size（X）；%n为样本数；m为指标数

Y＝X×PC%n个样本的m个综合因子（PC）得分

Y1＝X（：，：）×PC（：，1）%n个样本的第1个综合因子（PC）得分

Y2＝X（：，：）×PC（：，2）%n个样本的第2个综合因子（PC）得分

plot（Y1，Y2，＇.＇）；xlabel（＇第一主成分＇）；ylabel（＇第二主成分＇）；title（＇样本分类图＇）；

for ii＝1∶1∶n；text（Y1（ii），Y2（ii），［＇s＇，num2str（ii）］）；end

综合因子

特征值

某一综合因子解释方差占总方差的百分比%

从主成分分析图1中可看出：S2（二氧化氮）、S7（硫酸盐化速率）、S5（空气污染指数）、S8（pH值）占主要成份，是这几年对大同市环境污染的主要因素。那么未来是怎样的变化趋势呢？为此，对这八项污染因子作了以下进一步的预测分析。

图1 空气主要污染物样本分类

3 用灰色系统预测模型及其在MATLAB的实现

（1）对二氧化硫（mg／m3）二氧化氮（mg／m3）总悬浮物（mg／m3）降尘浓度（t／km2·30d）的预测分析：编制的MATLAB的程序如下。

disp（＇估计出的系统预测模型系统－微分方程组系数＇）

AA＝A

UU＝U（∶）

%调用微分方程组的求解命令求解微分方程组t0＝2001；tf＝2015；

y0＝［15.3 4.5 52 39.52］；

［tt，xx］＝ode15s（＠c4fun44，［t0，tf］，y0，［］）；

plot（tt，xx（∶，1），＇y－∧＇，tt，xx（∶，2），＇b－o＇，tt，xx（∶，3），＇g－＊＇，tt，xx（∶，4），＇r－p＇）；

legend（＇二氧化硫－预测＇，＇二氧化氮－预测＇，＇总悬浮物－预测＇，＇降尘浓度－预测＇）；

xlabel（＇年度＇）；ylabel（＇预测值＇）；hold on；

function dxt＝c4fun44（t，x）

global AA UU；

dxt＝AA＊［x（1）；x（2）；x（3）；x（4）］＋UU；

估计出的系统预测模型系统－微分方程组系数

从图2可看出降尘浓度有增长趋势。

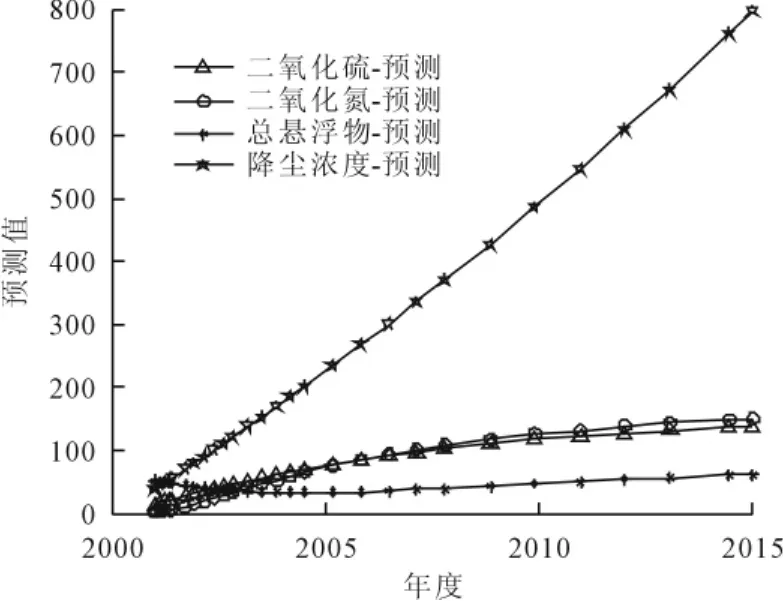
图2 空气主要污染物浓度预测图a

（2）对污染指数、可吸入颗粒物、硫酸盐化速率pH值的预测分析：

disp（＇估计出的系统预测模型系统－微分方程组系数＇）

AA＝A

UU＝U（∶）

%调用微分方程组的求解命令求解微分方程组

t0＝2001；tf＝2015；

y0＝［5.7 1.78 0.899 6.67］；

［tt，xx］＝ode15s（＠c6fun64，［t0，tf］，y0，［］）；

plot（tt，xx（∶，1），＇y－∧＇，tt，xx（∶，2），＇b－o＇，tt，xx（∶，3），＇g－＊＇，tt，xx（∶，4），＇r－p＇）；

legend（＇污染指数－预测，可吸入颗粒物－预测，硫酸盐化速率－预测，pH值－预测）；

xlabel（＇年度＇）；ylabel（＇预测值＇）；hold on；

function dxt＝c6fun64（t，x）

global AA UU；

dxt＝AA＊［x（1）；x（2）；x（3）；x（4）］＋UU；

c6fun6＿4

估计出的系统预测模型系统－微分方程组系数

从图3可看出盐化速率和可吸入颗粒物在逐步向上发展。

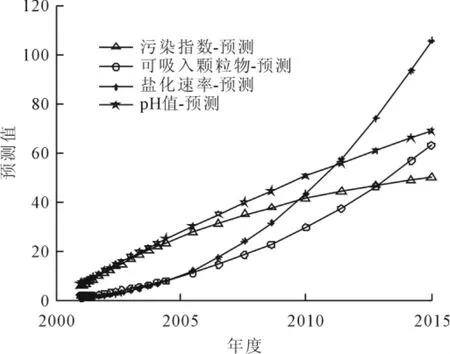
图3 空气主要污染物浓度预测图b

4 结语

根据图1主成分的表明，S2（二氧化氮）、S7（硫酸盐化速率）占主要污染物，预测图2、图3发现降尘浓度、盐化速率和可吸入颗粒物（PM10）的有增长趋势。但预测中二氧化氮在今后的变化趋势中并不明显，不作为分析的对象。

可吸入颗粒物（PM10）是最近环境各类媒体上，最热门的话题，PM10污染的形成不外乎两个途径。即污染源的贡献及自然条件，这些因素相互影响共同作用造成PM10污染。这几年PM10值的上升，与某市车辆的增加和城市的拆迁、扩建改造工程的加大也有一定的关系，根据有关资料表明，该市的2006年机动车数量为2.8063万辆；2007年机动车数量为3.1049万辆；2008年是3.483万辆。预测2012年车辆的可增达30多万辆。在近两年中，城市进行了大量的旧房拆迁及扩建工程，使降尘量增大，可吸入颗粒物也不断逐步向上发展，造成了浓度的增加。

城市的主要污染物是长期以来对城市居民健康造成直接的危害性，为更好地反映其污染变化趋势、加强污染防治工作和预防严重污染事件的发生，研究污染预测方法，这样的预测将给政府提供了科学有力的治理依据。可更好地开展污染预报及治理工作。为此，借助于MATLAB极强的非线性处理能力，来解决大气环境主要污染物自身复杂多变的问题，利用MATLAB技术应用到空气污染的主份因子分析及预测领域中，是很好的治理手段。

［1］ 宋新山，邓 伟，张 琳.MATLAB在环境科学中的应用［M］.北京：化学工业出版社，2008.

［2］ 吴 萍，陈作平，曾万明.汽车污染物排放的危害有对策［J］.科技视野，2008（9）：53.

［3］ 刘登国，居 力.机动车排气污染新标准颁布标准对管理模式变革的探讨［J］.环境监测管理与技术，2008（2）：5～6.