一个常见不等式的推广及其应用
2012-11-15黄华平胡松林湖北师范学院数学与统计学院湖北黄石435002
黄华平,胡松林(湖北师范学院 数学与统计学院,湖北 黄石 435002)
0 引言
众所周知,不等式不仅在数学的其它学科,诸如高等代数、微分方程、概率论、数理统计、离散数学、运筹学、复变函数、实分析与泛函分析等方面有重要的应用,而且在普通物理学、量子力学、材料学、建筑学等其它学科也有广泛的应用. 所以探讨各种不等式的性质,想办法把它应用到实际生活生产中显得尤为必要. 本文首先将初等数学中一个常用的不等式进行了各种形式的推广,然后给出了它的一些应用.
1 主要结果
初等数学中有这样一个不等式:
此式当且仅当x=y时取等号. 这是一个非常重要的不等式,在中学数学或高等数学中会经常碰到. 下面给出上述不等式的几种推广形式.
定理1 设p≥1,x≥0,y≥0,则有不等式:
(1)
此式当且仅当x=y或p=1 时取等号.
证明 当x=y=0 时不等式显然成立. 当x+y>0 时不等式(1)等价于
(2)

L(u,v,λ)=up+vp+λ(u+v-1)
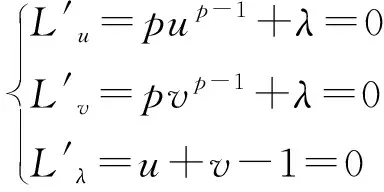

所以
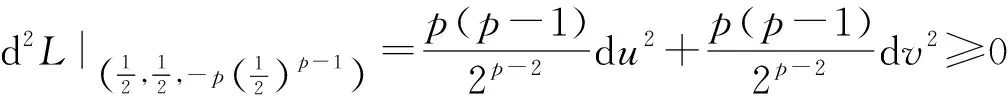

注意,上述证明过程首先考虑了将原不等式转化二元函数的条件极值问题,然后充分利用了Lagrange乘数法,从而将问题迎刃而解. 此方法有一定的优越性,但是计算量比较大. 下面首先给出(1)式的几种推广形式,然后给出了详细的证明过程. 证明中避开了利用Lagrange乘数法的解题思想,进而将问题大大简化.
定理2 设0≤λ≤1,x≥0,y≥0,p≥1,则有
λxp+(1-λ)yp≥[λx+(1-λ)y]p
(3)
此式当且仅当x=y或p=1 时取等号.
证明 当x,y中至少有一个为 0时,结论显然成立. 下设x>0,y>0, 将(3)式不等号两端同除以xp可得


(4)
下证(4)式成立. 事实上,令
f(t)=λ+(1-λ)tp-[λ+(1-λ)t]p
则f′ (t)=p(1-λ)tp-1-p(1-λ)[λ+(1-λ)t]p-1=p(1-λ){tp-1-[λ+(1-λ)t]p-1}
下面分两种情况讨论.
1)当t≥1 时,t≥λ+(1-λ)t,从而tp-1≥[λ+(1-λ)t]p-1,进而f′(t)≥0, 导致f(t) 在[1,+∞)上单调递增,于是f(t)≥f(1)=0,即得(4)式.
2)当t≤1 时,t≤λ+(1-λ)t,从而tp-1≤[λ+(1-λ)t]p-1,进而f′(t)≤0, 导致f(t)在 (0,1]上单调递减,于是f(t)≥f(1)=0,即得(4)式.
推论1 设α,β≥0,α+β=1,x,y≥0,p≥1,则有
αxp+βyp≥(αx+βy)p
(5)
此式当且仅当x=y或p=1 时取等号.
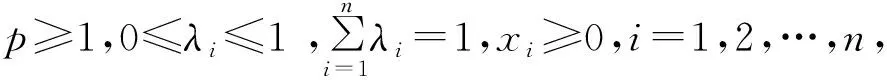
(6)
此式当且仅当x1=x2=…=xn或p=1 时取等号.
证明 当n=1 时结论显然成立. 当n=2 时,由推论1得到结论也成立. 下面先假设(6)式成立,要证


由(6)式和(5)式得到

(λ1x1+λ2x2+…+λn+1xn+1)p
最后由数学归纳法即得结论.
注1 显然(6)式将(5)式进行了大大的推广.
注2 上述各结论中,若p<0 ,其它条件不变,则不等号同样成立;若0 定理4 设p≥1,x≥0,y≥0,则 xp+yp≤(x+y)p≤2p-1(xp+yp) 当且仅当p=1时上式都取等号. 证明 首先,直接由(1)式得出 (x+y)p≤2p-1(xp+yp)(x,y≥0) 故只需证 xp+yp≤(x+y)p(x,y≥0) (7) 1+tp≤(1+t)p (8) 推论2 设p≥1,0≤x≤1, 则 当且仅当p=1 时上式都取等号. 证明 由定理4得 由于 0≤x≤1, 上式取y=1-x即得结论. 或者这样证:考虑f(x)=xp+(1-x)p在[0,1] 上的最大值和最小值即可. 定理5 设p≥1,xi≥0,i=1,2,… ,n,则 当且仅当p=1 时上式都取等号. 下证 (9) 事实上,当n=1 时显然成立. 当n=2 时,即为(7)式. 下面假设(9)式成立,然后由(7)式和(9)式得到 于是由数学归纳法即得(9)式. 注 当0 其中x=(x1,x2,…,xn,…)∈lp,y=(y1,y2,…,yn,…)∈lq. 定理6 设x=(x1,x2,…,xn,…)∈lp,y=(y1,y2,…,yn)∈lq, 若规定 xy=x1y1+x2y2+…+xnyn+… 则 ‖xy‖1≤‖x‖p‖y‖q≤‖x‖1‖y‖1 证明 ‖xy‖1≤‖x‖p‖y‖q即为引理1中的Hölder不等式. 下证 ‖x‖p‖y‖q≤‖x‖1‖y‖1 (10) 由定理5得到 上式不等号两边分别让n→∞ ,得到 ‖x‖p≤‖x‖1,同理可得‖x‖q≤‖y‖1.此两式相乘即得(10)式. 定义1[5]设X为一个非空集合,K≥1为一常数. 如果映射ρ:X×X→[0,+∞)对于∀x,y,z∈X,满足下述条件: i)ρ(x,y)≥0,∀x,y∈X,ρ(x,y)=0⟺x=y; ii)ρ(x,y)=ρ(y,x); iii)ρ(x,y)≤K[ρ(x,z)+ρ(z,y)]. 则称(X,ρ) 为度量型空间. 注 当K=1 时,度量型空间退化为度量空间,从而可以知道度量型空间是度量空间的大大推广. 例1 设p≥1,X=K,K为实数域或复数域. 定义 则 (X,ρ)为度量型空间. 证明 定义1中的i)、ii)显然成立. 下面只验证iii). 如下: ∀x,y,z∈X,由(1)式得到 从而 ρ(x,y)≤2p-1[ρ(x,z)+ρ(z,y)] 所以结论成立. 例2 设ai≥0,i=1,2,… ,9,证明 证明 注意到 于是由定理3即得结论. 参考文献: [1]朱来义.微积分(第三版)[M]. 北京:高等教育出版社, 2009. [2]陈庆华.高等数学(第一版)[M]. 北京:高等教育出版社, 1999. [3]华东师范大学数学系.数学分析[M]. 北京:高等教育出版社, 2002. [4]张恭庆,林源渠.泛函分析讲义(上册) (第一版) [M]. 北京:北京大学出版社, 1987. [5]Khamsi M A, Hussain N. KKM mappings in metric type spaces[J].Nonlinear Analysis,2010, 73: 3123~3129.


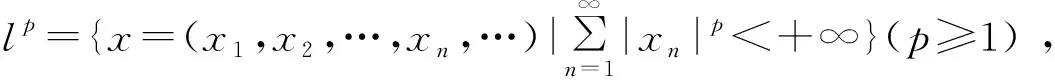

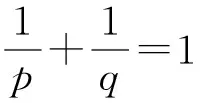
2 应用


