椭球膨胀法在区域控制网投影计算中的应用

2012-11-15李陆勋

测绘通报 2012年5期

关键词：椭球面椭球纬度

李陆勋

(国家林业局昆明勘察设计院，云南昆明650216)

椭球膨胀法在区域控制网投影计算中的应用

李陆勋

(国家林业局昆明勘察设计院，云南昆明650216)

对基于椭球膨胀法的区域控制网投影计算进行研究，并对椭球长半轴变量Δa的计算和取值、膨胀椭球对大地经度、纬度、大地高的影响等进行分析。基于对Δa、dB的取值和影响分析，提出简化计算方法，并进行计算验证。研究成果对高海拔地区应用椭球膨胀法建立区域控制网具有参考价值。

椭球膨胀;区域控制网;投影计算

一、引言

应用GPS建立工程控制网、城市相对独立坐标系等区域控制网时，需将椭球面上的大地坐标经高斯投影转换为平面坐标。低海拔地区可以直接采用标准椭球面作为计算基准面，而高海拔地区若直接采用标准椭球面作为计算基准面，则会使地面长度的投影变形较大，地面实测距离与控制点坐标反算的距离差异较大，难以满足实际或工程上的需要，计算和使用都不方便。为减小边长投影变形，通常采用两种方法:一种是以测区的平均高程面(或抵偿高程面、测区最低高程面)作为边长投影计算基准面;另一种是采用变换椭球法。变换椭球法可以在标准椭球和区域椭球间建立严密的数学关系，更适合于采用GPS测量建立区域控制网。常用的变换椭球法有膨胀法、平移法、变形法。其中，膨胀法计算简便，可以较好地解决高海拔地区建立区域控制网的高程投影问题［1-2］。

二、椭球膨胀法原理

如图1所示，E0为原标准椭球面，P0为地面上的基准点，E0沿P0的法线方向膨胀Δh到定义的参考面Ph(测区平均高程面或最低高程面)，Δh为图中J1到J2点的距离，即在E0椭球下沿P0的法线方向穿过参考面Ph的距离。膨胀前后，椭球中心保持不动，椭球扁率α保持不变，椭球长半轴变化Δa= aE1－aE0。由于椭球面具有各向异性，所以椭球膨胀后原法线P0→J1在E1下不一定再与椭球面E1垂直。

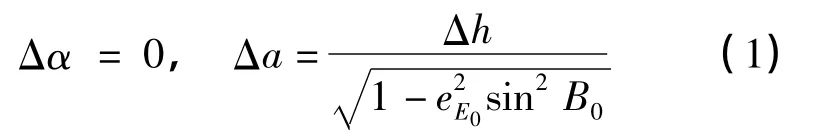
已知广义大地坐标微分公式

式中，A、B、C、D的计算参见文献［3］。

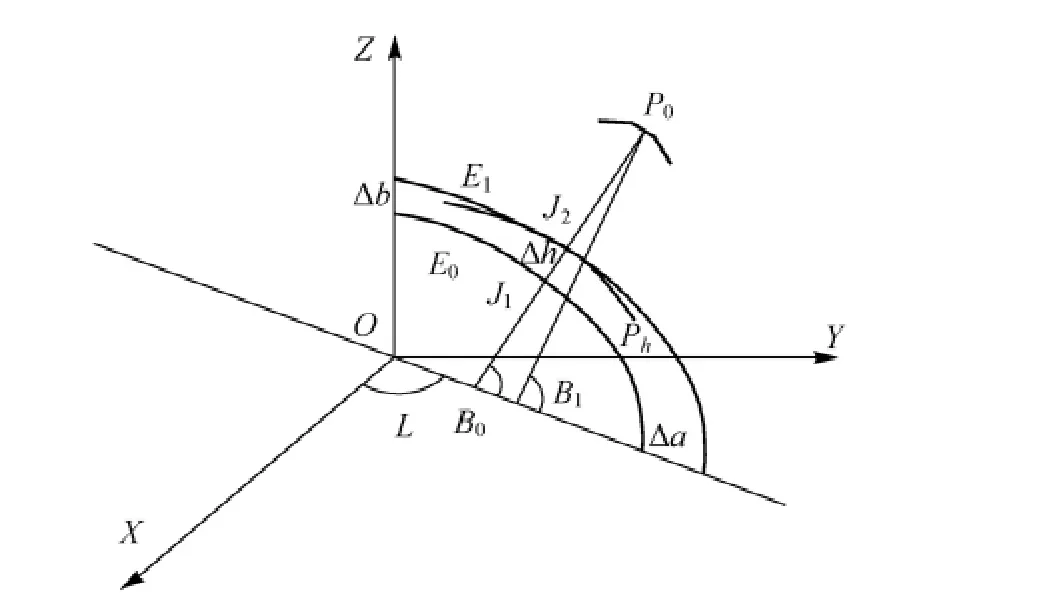
图1 椭球膨胀法

由椭球膨胀法可知

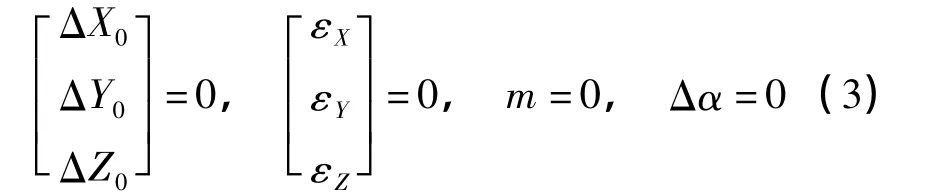
则

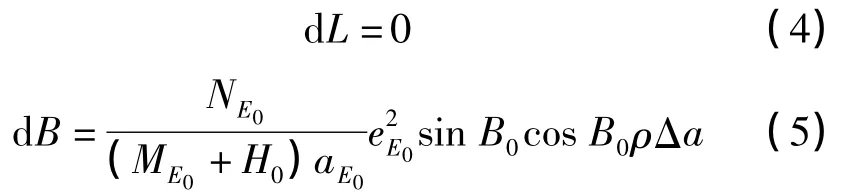
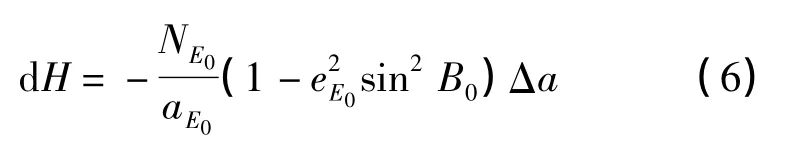
即膨胀法对大地经度L没有影响，只对纬度B和大地高H有影响。在新椭球E1下，可以重新计算新的(B，L，H)E1，以新椭球的参数作高斯投影，计算新的(x，y)E1。

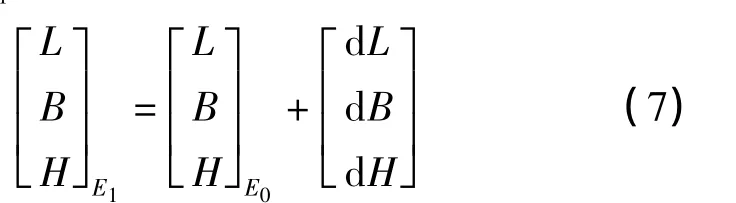
三、椭球膨胀法投影计算思路

已知区域控制网各控制点在标准椭球中的经纬度以及控制网平均高程面Hm，将标准椭球面高程视为0 m，可得Δh=Hm，利用式(1)计算得Δa，进而计算区域椭球的各项参数，建立区域椭球，应用式(7)计算各点在区域椭球中的经纬度，在区域椭球下作高斯投影计算，即得到各控制点在平均高程面Hm上的坐标。为简化计算，实际计算时取Δa=Hm。

该方法的实质是利用膨胀椭球、高斯投影，将点坐标投影至需要的高程面，并在两个高程面之间建立严密的数学关系，可以方便地进行正反算，使得区域控制网的独立坐标与国家大地坐标之间可以互相换算，省去了边长投影计算过程，同时便于区域内不同独立坐标系间的转换。

四、Δh、Δa取值分析

用椭球膨胀法建立区域椭球时，椭球长半轴变量Δa通常由式(1)和测区平均纬度严密计算得到。

如图2所示，根据椭球膨胀法原理可知，Δh是测区在标准椭球上的平均大地高，而测区平均高程面采用的是正常高，两者差值为高程异常值ξ。如果已知测区范围内的高程异常值ξ，则可精确计算得椭球面高差Δh，但我国目前的似大地水准面模型分辨率和精度分布不均，西部高海拔地区还存在大量的数据空白地区，西部精确的高程异常值ξ难以获得;另外，我国1954北京坐标系对应的参考椭球高程异常平均为29 m，1980西安坐标系对应的参考椭球高程异常平均为10 m［9］。当ξ=29 m时，其对区域椭球高斯投影坐标的影响主要反映在北坐标x上，从边长投影角度看，该值对边长投影的影响约为1/220000，而区域控制网覆盖范围较小，测区内ξ值差异不大，即ξ值对区域控制网边长投影计算的误差影响可以忽略，计算时，Δh一般可取为测区平均高程面。

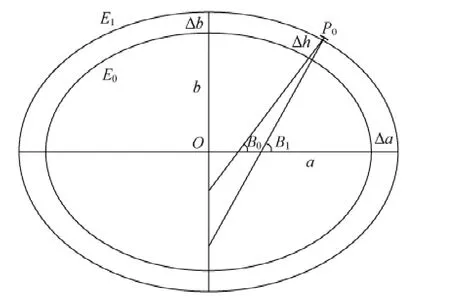
图2 椭球膨胀法简化应用示意

以克氏椭球为例，由式(1)计算得到的Δa与Δh的差值随纬度、平均高程面的增加而增加。当B =0°时，Δa－Δh=0;当B=90°时，Δa－Δh达到最大，其对应关系如表1所示。

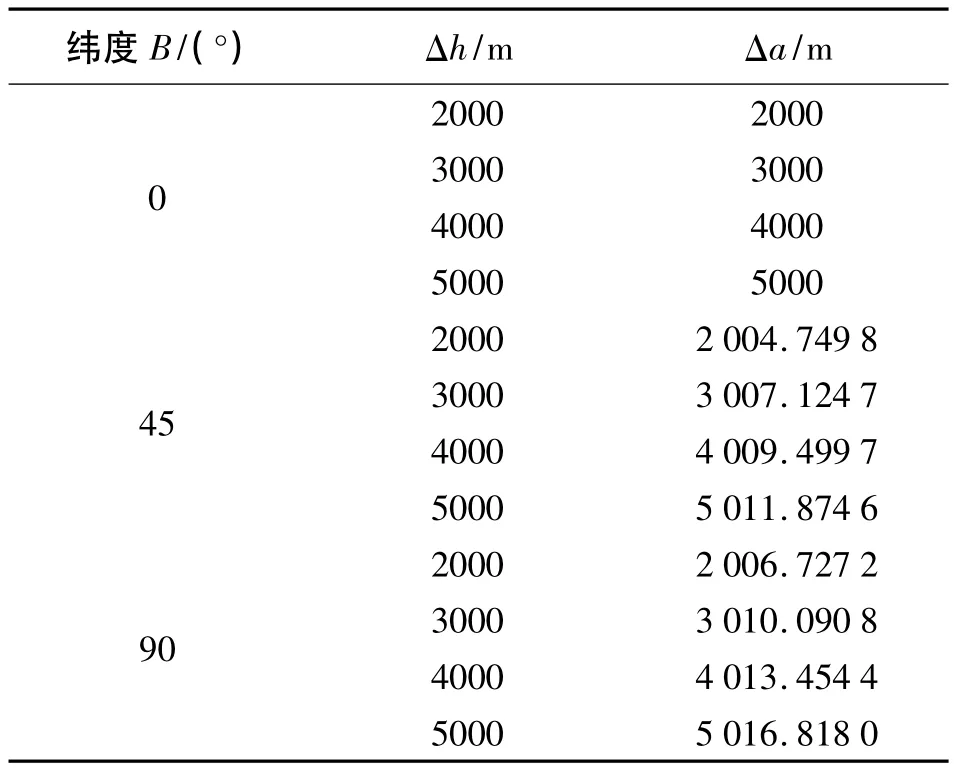
表1 克氏椭球不同纬度、高程情况下Δh、Δa的对应关系

由表1可看出，极端情况下，当B=90°，Δh= 5000 m时，Δh与Δa的差值最大，为16.818 m。一般Δh与Δa的差值在10 m以内，该差值对边长投影计算的影响约为1/630 000，可以忽略，因此在实际应用时可取Δa=Δh，以简化计算过程。

五、dB影响分析

应用椭球膨胀法建立区域椭球，dB的变化趋势是当B=0°和B=90°时，dB=0;当B=45°时，dB达到最大，如表2所示。

区域控制网覆盖范围较小，公路、铁路等线路工程在南北向布设时，其纬度跨度才比较大，我国的高原主要集中于北纬20°～40°，表3列出了B= 40°、B=41°，Δa=2000 m时的dB值及其差值。

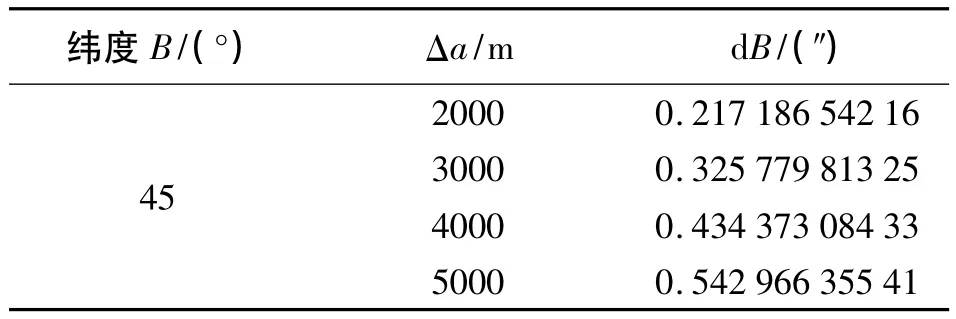
表2 B=45°时的各高程dB值(克氏椭球)

表3 B=40°、B=41°、Δa=2000 m时的dB值及差值(克氏椭球)

从表3可看出，测区纬度跨度1°时，dB差值约为0.001 161 700 57″，相当于地面距离0.034 85 m，已知地球椭球纬度跨度 1°时，地面距离约为111 km，dB差值对距离的影响约为1/3 180 000。尽管dB绝对值较大，对坐标绝对值的影响达到米级，但其相对差值较小，可以忽略。因此，区域控制网在应用膨胀椭球法进行高斯投影计算时，可以不考虑dB的影响，

六、计算验证

基于上述分析，取有代表性的任意两个点对椭球膨胀法简化计算进行验证。已知 P1(40°N，99°E)、P2(41°N，99°E)两点，中央子午线99°，平均高程面Hm=2000 m，不考虑高程异常值，按两种方法进行投影计算:方法一为Δh=Hm，用式(1)和两点的平均纬度计算Δa，考虑dB的影响;方法二采用简化计算，即Δa=Hm，不考虑dB的影响。计算结果如表4所示。

表4 椭球膨胀法简化计算验证(克氏椭球)

上述两种方法计算得到的P1点x相差9.6441 m，P2点 x相差 9.757 1 m，方位角一致，距离相差0.113 m，距离相对误差为1/980 000。考虑dB时点位往北移。采用简化算法时，控制网整体往南移，但不影响点位坐标精度和相对关系。

七、结束语

椭球膨胀法原理建立在广义大地坐标微分公式基础上，具有严密的数学基础。应用椭球膨胀法建立区域控制网，可以较好地解决高海拔地区建立区域控制网的高程投影问题，使区域控制网坐标系与国家大地坐标系之间建立起严密的数学关系，便于不同坐标系间的相互转换。对于区域控制网，可以使用简化的椭球膨胀法进行投影计算，即计算时取(B，L)E0=(B，L)E1，Δa=Hm。

［1］李世安，刘经南，施闯.应用GPS建立区域独立坐标系中椭球变换的研究［J］.武汉大学学报:信息科学版，2005，30(10):888-891.

［2］柴军兵，丁翔宇，彭永超，等.椭球膨胀法在GPS测量中的应用［J］.测绘通报，2009(12):34-36.

［3］孔祥元，郭际明，刘宗泉.大地测量学基础［M］.武汉:武汉大学出版社，2002.

［4］孔祥元，郭际明.控制测量学［M］.3版.武汉:武汉大学出版社，2010.

［5］程鹏飞，成英燕，文汉江，等.2000国家大地坐标系实用宝典［M］.北京:测绘出版社，2008.

［6］丁士俊，畅开蛳，高琐义.独立网椭球变换与坐标转换的研究［J］.测绘通报，2008(8):4-6.

［7］海清.通过椭球变换建立区域独立坐标系的方法［J］.测绘与空间地理信息，2008，31(1):168-169.

［8］邓兴升，汤仲安，花向红，等.椭球变换后的高斯投影正反算算法［J］.大地测量与地球动力学，2010，30(2):49-52.

［9］边少锋，柴洪洲，金际航.大地坐标系与大地基准［M］.北京:国防工业出版社，2005，55-57.

［10］施一民，周拥军，张文卿.用定向定位调整法确定区域性椭球面［J］.测绘学报，2002，31(2):118-122.

The Application of Ellipsoid Expansion Method in the Calculation of Region Control Network Projection

LI Luxun